
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графическое определение погрешностейСодержание книги
Поиск на нашем сайте Если изучается зависимость одной величины от другой, то результаты могут быть представлены в виде графика. Основное достоинство графиков – их наглядность. Посмотрев на график, можно сразу, одним взглядом, охватить вид полученной зависимости, получить о ней качественное представление и отметить наличие различных особенностей: максимумов и минимумов, областей возрастания и убывания, периодичности и т.п. График позволяет также судить о соответствии экспериментальных данных той или иной теоретической зависимости. При вычерчивании графика в прямоугольной системе координат необходимо руководствоваться следующими правилами. 1. Выбор бумаги. График должен выполнятся на миллиметровой или хотя бы клетчатой бумаге. 2. Выбор координатных осей. По горизонтальной оси принято откладывать ту величину, изменения которой являются причиной изменения другой (т.е. по оси абсцисс – аргумент Х, по оси ординат – функцию Y). На осях координат следует указать название или символ величины и указать, в каких единицах она измеряется:
3. Выбор интервала. На графике приводится только та область изменения измеряемых величин, которая была исследована на опыте, поэтому пересечение координатных осей не обязательно должно совпадать с нулевыми значениями Х = 0 и Y = 0. Например:
4. Выбор масштаба. Масштабы на каждой оси выбираются независимо друг от друга, причем так, чтобы экспериментальные точки не сливались друг с другом и чтобы наилучшим образом использовалась площадь бумаги. Следует помнить, что график получается более наглядным, если основная часть кривой имеет наклон, не слишком отличающийся от 45º. Масштаб должен быть простым и легко читаться, поэтому одна клетка масштабной сетки должна соответствовать удобному числу – 1, 2, 5, 10 …, 0,1, 0,2, 0,5, (но не 3, 7, 11, 13 …), единиц изображаемой на графике величины. 5. Нанесение шкал по осям. Масштаб наносится на осях графика в виде равностоящих “круглых” чисел, например:
или
Не следует расставлять эти числа слишком густо – достаточно нанести их через 2 или даже через 5 делений:
6. Нанесение точек на график. На график наносят все полученные в измерениях значения. Если одна точка измерялась несколько раз, можно нанести среднее и указать погрешность. Координаты экспериментальных точек на осях выписывать не нужно, т.к. это загромождает график и мешает его чтению (на осях наносятся только масштабные деления). Выносные линии на графике, как правило, не проводятся: научитесь наносить точки на график без их помощи. Выносная линия может в виде исключения быть нанесена, только если какую-либо точку хотят особо выделить на графике. Размечать масштабные деления на осях координат и наносить на график точки лучше всего сначала карандашом. Вдруг вы решите изменить масштаб или окажется, что какая-то точка случайно поставлена неправильно. Если же с масштабом и расположением точек все в порядке, нетрудно обвести все чернилами. В результате же удается избежать переделок и лишних затрат графической бумаги. 7. Проведение кривой по нанесенным точкам. Так как все измерения сделаны с той или иной погрешностью, то может наблюдаться некоторый разброс точек. Нельзя соединять эти точки простой ломаной линией, проходящей через каждую точку, т.к. это означало бы, что зависимость между двумя величинами носит скачкообразный характер, а это маловероятно. Скорее следует ожидать, что данная зависимость описывается какой-либо плавной кривой. Помните, что всякая особенность на кривой (излом, резкое изменение кривизны и т.д.) требует специального экспериментального доказательства, либо теоретического объяснения. Поэтому чаще всего кривую на графике проводят плавно, избегая изломов и перегибов, причем так, чтобы большее число экспериментальных точек легло на эту линию, а остальные равномерно распределились выше и ниже ее. Во всех случаях кривая должна быть проведена так, чтобы она не закрывала экспериментальных точек. Помните, что результат эксперимента - это точки, а кривая – это только Ваше толкование результата (вообще говоря, не однозначное). 8. Выбор наиболее наглядной зависимости. При построении графика нужно стремиться к тому, чтобы он наиболее четко отображал все особенности представляемой зависимости. Для этого часто бывают удобны функциональные масштабы – по осям откладываются не сами измеряемые величины, а их функции, подобранные в соответствии с решаемой задачей. Например, если измеряемая величина изменяется очень сильно, на несколько порядков, удобно применять логарифмический (по осям откладываются логарифмы измеряемых величин) или полулогарифмический масштаб (логарифм откладывается только по одной из осей). С примером полулогарифмической шкалы Вы встретитесь в работе по снятию аудиограммы и частотной характеристики импеданса биологической ткани. При пользовании функциональных масштабов на оси следует наносить двойную шкалу: одну – равномерную для откладываемой по оси функции (например, lg x), а другую – неравномерную для самой величины (но и на эту шкалу наносят, как обычно, “круглые” числа.
9. Оформление графиков. Готовый график, снабжается подписью, которая должна содержать точное описание того, что показывает график. Ниже показан пример построения графика (к лаб. раб.№ 1).
Рисунок 1. Зависимость чувствительности α весов от Величины нагрузки P
11. На основании графика можно найти абсолютную погрешность в определении одной из величин, если известна абсолютная погрешность другой величины. Пусть график изображает зависимость y = f(x) и известно, что некоторое значение величины Х измерено с погрешностью Δх (точка Х0). Тогда на графике откладывают на соответствующей оси около значения Х0 величину ΔX в выбранном масштабе и по графику находит соответствующую ей величину отрезка ΔY (см. рис.2). Найденное ΔY и будет представлять собой абсолютную погрешность в определении Y.
Задачи для самостоятельного решения 1. Постоянная термопары определяется по формуле
где Rr – сопротивление гальванометра 30 Ом, I – ток термопары (показания гальванометра) T2 - T1 – разность температур теплого и холодного слоев термопары: T1 - T2 = 10 К. По показаниям гальванометра оцените среднее значение и погрешность измерения ˚ С при γ = 0,95 I · 10-10 А: 23; 24; 23,5; 25; 24,2.
2. Коэффициент вязкости жидкости определяется формулой (капиллярный вискозиметр): где t2 – время истечения из капилляра исследуемой жидкости объемом V; t1 - время истечения из капилляра дистиллированной воды объемом V; Обработать данные при
t1 = 9,8 10 10,2 9,9 9,9 t2 = 38,8 40,2 40 40,3 40,5
3. Определить размеры коллоидной частицы по скорости ее оседания в монодисперсной среде из формулы Стокса (
где
g - ускорение силы тяжести (9,8 м/сек2).
Скорость оседания в пяти измерениях составила:
4. Вес тела при взвешивании по методу Гаусса определяется по формуле где: P1 – вес тела на левой стороне весов [г], P2 – вес тела на правой стороне весов [г].
В результате взвешивания получены результаты: P1 = 2,32 г, 2,21 г, 2,25 г, 2,24 г, 2,23 г. P 2 = 2,41 г, 2,39 г, 3,4 г, 2,41 г, 2,42 г. Найти
5. При определении к.п.н. методом отрыва капель формула для его подсчета имеет вид: Где:
Лабораторная работа №1
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.011 с.) |


 или
или
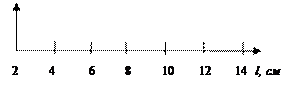


 Дополнительно указывать масштаб, как это делается на географических картах, не следует.
Дополнительно указывать масштаб, как это делается на географических картах, не следует. Например:
Например:
 10. Кривую, построенную по экспериментально полученным точкам для некоторой области изменения аргумента, можно затем использовать для нахождения значений функции для любого промежуточного значения аргумента на этой области. Эта операция называется графическим интегрированием. Например, по графику (рис. 1) можно найти значение чувствительности весов αх при нагрузке Рх = 75 г: α 75 =
10. Кривую, построенную по экспериментально полученным точкам для некоторой области изменения аргумента, можно затем использовать для нахождения значений функции для любого промежуточного значения аргумента на этой области. Эта операция называется графическим интегрированием. Например, по графику (рис. 1) можно найти значение чувствительности весов αх при нагрузке Рх = 75 г: α 75 = 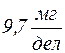 .
. ,
, ,
, и известных
и известных (вода)
(вода) (кровь)
(кровь)

 )
)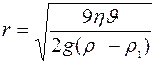 ,
, - коэффициент вязкости среды (4 сПз),
- коэффициент вязкости среды (4 сПз),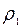 - плотность среды (0,95 г/см3),
- плотность среды (0,95 г/см3),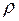 - плотность частицы (3 г/см3),
- плотность частицы (3 г/см3),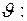 8,1 8,25 8,3 8,2 8,15 мм/час.
8,1 8,25 8,3 8,2 8,15 мм/час.
 и
и 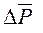 , при
, при 

 - плотность эталонной жидкости (1 г/см3),
- плотность эталонной жидкости (1 г/см3), - плотность исследуемой жидкости (1,5 г/см3).
- плотность исследуемой жидкости (1,5 г/см3).


