
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рассмотрим некоторые из названных и другие величиныСодержание книги
Поиск на нашем сайте Угловая скорость При изменении угловой скорости вводят понятие углового ускорения:
Угловое ускорение
Т.к. где Для характеристики динамики вращательного движения вводятся понятия мо мента силы и момента инерции. Рассмотри движение материальной точки " А " с массой m по окружности радиусом r (рис. 1). Пусть на точку " А " массой m действует сила Ft = F Sina = m Так как F Sina = mre (2) Умножив правую и левую часть равенства (2) на r получим: Fr Sina = mr2e или M =Je, отсюда:
где М=FrSina или в векторной форме:
Рисунок 1. Вращение материальной точки А массой m относительно оси «О» Зависимость
Для тел различной геометрической формы момент инерции рассчитывается по формулам, полученных при интегрировании выражения (4). Для примера рассчитаем момент инерции однородного стержня длиной l и массой m, когда ось вращения ОО проходит через его середину

Рисунок 2. Момент инерции тонкого прямого стержня относительно его центральной оси, перпендикулярной к стержню На расстоянии х от оси вращения выделяем малый участок стержня длиной dx масса этого участка равна dm, тогда согласно формуле (4), момент инерции для этого участка запишется в виде
Для определения dm вводим линейную плотность, как Момент инерции для всего стержня запишется в виде:
Если ось вращения тела О1О1 параллельна оси симметрии ОО, но смещена от нее на расстояние d, то момент инерции I, относительно новой оси О1О1 определяется по теореме Штейнера
где I0 - момент инерции тела относительно оси симметрии. рассчитаем момент инерции для однородного тонкого стержня длиной l и массой m, когда ось вращения проходит перпендикулярно к стержню через его конец
тогда
Рисунок 3. Момент инерции тонкого прямого стержня относительно оси.
Для других однородных тел геометрически правильной формы массой m относительно оси симметрии момент инерции рассчитывается по формулам: 1)для однородного сплошного цилиндра (диска) относительно продольной оси J=mR2/2, где m - масса цилиндра, R - его радиус; 2 ) для однородного шара радиуса R, массой m относительно оси, проходящей через его середину 3 ) для тонкого однородного кольца (обруча) радиуса R массой m относительно оси, проходящей через центр перпендикулярно к плоскости кольца J = mR2 и т.д. Для тел геометрически неправильной формы массы m момент инерции определяется экспериментальным путем. Основное уравнение динамики вращательного движения тела можно записать в ином виде, учитывая, что
Величина Приведенное равенство (5) показывает, что изменение момента количества движения вращающегося тела равно импульсу момента приложенных к нему сил. Если Это следствие называется законом сохранения момента количества движения: если сумма моментов сил Изучение законов вращательного движения в лабораторной работе производится с помощью маятника Обербека, который представляет собой крестовину, состоящую из 4-х стержней каждый длиной l/2, прикрепленных к втулке с осью (рис.4). На стержнях фиксируются грузы массой m1, которые могут быть закреплены симметрично на различных расстояниях от оси вращения. На шкив радиусом r, находящийся на оси вращения, наматывается нить, к свободному концу которой прикрепляется груз Р. Если предоставить грузу Р возможность двигаться, то это падение будет происходить с ускорением а. При этом шкив со стержнями и расположенными на них грузами будет вращаться с угловым ускорением e, которое можно найти, измерив высоту h и время падения груза t.
где r - радиус шкива, на который наматывается нить. Силой, создающей вращающий момент, является сила натяжения нити Т. Из второго закона Ньютона для груза Р следует
T = P - ma = mg - ma = m(g-a) (7) Тогда вращающий момент M = Tr = m(g-a)r (8) Момент инерции маятника может быть определен из основного уравнения вращательного движения: J=M/e (9) Подставляя в формулу (9) формулы (5) и (7) получим окончательное выражение для момента инерции маятника Обербека, определенного практически (экспериментально):
С другой стороны, теоретически, момент инерции маятника может быть найден из формулы Jтеорет Тогда момент инерции крестовины теоретически определяется по формуле:
где m2 - масса «двойного» стержня, l – его длина (см. рис.4). Выполнение работы 1. Грузы m1 на маятнике Обербека (крестовине) закреплены на некотором одинаковом расстоянии R от оси вращения (рис.4). 2. Измерить расстояние R от оси вращения до центра масс груза m1. 3. Намотать нить на шкив крестовины и последнюю придерживать рукой. 4. Подвесить к нити груз массой m (100, 200 или 300 гр) и совместить нижнюю часть груза с верхней меткой на стене. 5. Дать возможность грузу массой m опускаться. Измерить время движения t груза на расстоянии h = 0,5 м от верхней до нижней меток на стене. 6. Результаты измерений занести в таблицу 1. 7. Измерения провести при двух различных грузах массой m по 3 раза с каждым при h=const. 8. По формулам 11, 12, 13 (см. ниже) по средним значениям «t» вычислить линейное ускорение «a», угловое ускорение «e», вращающий момент «M», действующий на маятник
где r – радиус шкива, на который наматывается нить.
9. По формуле «14» высчитать момент инерции, найденный практически Jпракт = М / e (14)
10. Вычислить теоретически момент инерции «Jтеорет» по формуле (15) и сравнить с результатом Jпракт, полученным в пункте 9 (формула 14).
Сравнивая Jпракт = М/e, найденный из основного уравнения динамики вращательного движения (e= M/J), с его теоретическим значением
11. Вычислить абсолютную по формуле (16) и относительную по формуле (17) погрешность измерений для одной из серий результатов. Вычисление погрешностей 1) Абсолютная погрешность измерения практического значения момента инерции маятника Обербека:
где 2) Относительная погрешность измерения практического значения момента инерции маятника Обербека:
Таблица 1 Результаты измерений и вычислений
m1=154 г = 0,154 кг – масса каждого груза на стержне, m2 =184 г=0,184 кг – масса каждого из 2-х стержней, l =52 cм=0,52 м – длина стержня, r =1 см=0,01м – радиус шкива, g =9,8 м/с2, h =0,5 м, Dh =1см=0,01м
Рисунок 4. Маятник Обербека
Контрольные вопросы 1. Перечислите величины, характеризующие кинематику вращательного движения, момент инерции и единицы его измерения. 2. Момент инерции различных тел (с выводом формул для стержня, тонкого кольца, тонкой сферы и др.). 3. Момент силы (векторная форма записи), направление и единицы его измерения. 4. Основное уравнение динамики вращательного движения. 5. Закон сохранения момента количества движения (привести примеры использования его на практике). 6. Сочленения и рычаги в опорно-двигательном аппарате человека. 7. Центрифугирование.
Лабораторная работа №2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.01 с.) |

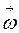 - вектор, численно равный dj / dt и направленный по оси вращения по правилу правого винта (если рукоятку правого винта вращать по направлению вращения тела, то направление поступательного движения винта покажет направление угловой скорости). Единицей измерения
- вектор, численно равный dj / dt и направленный по оси вращения по правилу правого винта (если рукоятку правого винта вращать по направлению вращения тела, то направление поступательного движения винта покажет направление угловой скорости). Единицей измерения 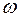 является [
является [ 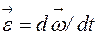 [ e ] = 1 рад/с2 (1/с2).
[ e ] = 1 рад/с2 (1/с2).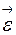 - вектор, совпадающий по направлению с угловой скоростью при ускоренном движении и противоположной ей – при замедленном. Угловое ускорение связано с тангенциальным (касательным) ускорением
- вектор, совпадающий по направлению с угловой скоростью при ускоренном движении и противоположной ей – при замедленном. Угловое ускорение связано с тангенциальным (касательным) ускорением  :
: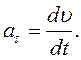
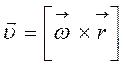 , то
, то 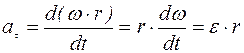 ,
, - линейная скорость
- линейная скорость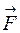 , лежащая в плоскости, перпендикулярной оси вращения О. Тогда точка приобретает постоянное тангенциальное ускорение аt, определяемое тангенциальной составляющей силы
, лежащая в плоскости, перпендикулярной оси вращения О. Тогда точка приобретает постоянное тангенциальное ускорение аt, определяемое тангенциальной составляющей силы 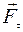 :
: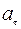 (1)
(1)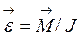 , (3)
, (3)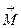 = [
= [ 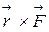 ] - вращающий момент (момент силы
] - вращающий момент (момент силы 
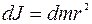 , тогда:
, тогда: или
или  (4)
(4)
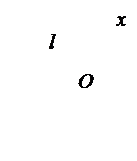

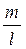 , тогда
, тогда 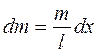 , а момент инерции
, а момент инерции 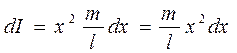
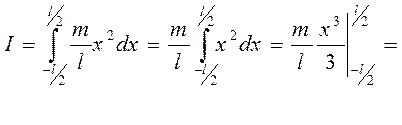
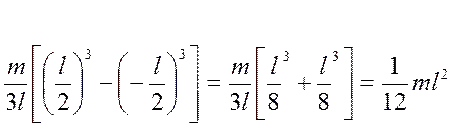
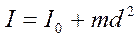
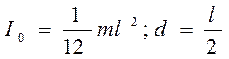 ;
;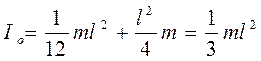

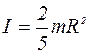
 ,
, 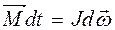 или
или (5)
(5) называется импульсом момента сил, приложенных к телу, а d (
называется импульсом момента сил, приложенных к телу, а d (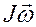 ) - изменение момента количества движения тела (момента импульса тела).
) - изменение момента количества движения тела (момента импульса тела).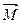 = О, то d (
= О, то d (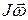 ) = 0 или
) = 0 или  , т.е. момент количества движения остается постоянным.
, т.е. момент количества движения остается постоянным.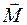 , действующих на тело, равна нулю (
, действующих на тело, равна нулю ( остается постоянным (
остается постоянным (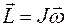 = const, то угловая скорость вращения тела
= const, то угловая скорость вращения тела  (6)
(6)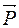 +
+ 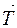 = m
= m 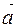 . Переходя от векторной суммы к алгебраической, проектируя на ось ОХ имеем: Р - Т = ma, откуда
. Переходя от векторной суммы к алгебраической, проектируя на ось ОХ имеем: Р - Т = ma, откуда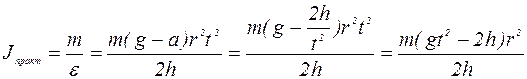 . (10)
. (10) Jk + 4Jr p (моментом инерции цилиндра радиуса r пренебрегаем), где Jk - момент инерции крестовины, Jrр - момент инерции груза относительно оси вращения. Считая груз материальной точкой массой m1, его момент инерции можно найти по формуле Jrp= m1R2, где R - расстояние от оси вращения до центра масс груза.
Jk + 4Jr p (моментом инерции цилиндра радиуса r пренебрегаем), где Jk - момент инерции крестовины, Jrр - момент инерции груза относительно оси вращения. Считая груз материальной точкой массой m1, его момент инерции можно найти по формуле Jrp= m1R2, где R - расстояние от оси вращения до центра масс груза.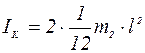

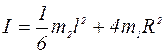 (11)
(11) (12)
(12) (13)
(13) (15)
(15)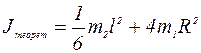 в работе проверяется справедливость основного уравнения динамики вращательного движения e = M/J.
в работе проверяется справедливость основного уравнения динамики вращательного движения e = M/J.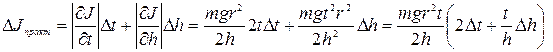 , (16)
, (16) .
. (17)
(17)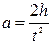 м/с2
м/с2
 a/r
1/с2
a/r
1/с2
 кг.м2
кг.м2
 кг.м2
кг.м2




