
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение центрированной оптической системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные понятия и определения: понятие тонкой линзы, оптической силы и светосилы линзы, линейное увеличение; сферическая аберрация, хроматическая аберрация, астигматизм; дальнозоркость и близорукость. Цель работы: различными методами научиться определять фокусные расстояния линз.
Краткая теория Линза представляет собой прозрачное тело, ограниченное двумя сферическими поверхностями (или поверхностью и плоскостью. В работе различных медицинских оптических приборов (микроскопы, эндоскопы, бронхоскопы, гастроскопы, очки и др.) нашли широчайшее использование как собирающие, так и рассеивающие линзы. Линза является собирающей, если она преломляет проходящие через нее лучи в сторону оптической оси, и рассеивающей, если она отклоняет лучи от оптической оси (рис.1).
Рисунок 1. Ход лучей в собирающей и рассеивающей линзах Рассматривая элементарную теорию преломления световых лучей на каждой из сферических поверхностей, ограничивающих тонкую линзу (тонкими линзами считают такие, у которых расстояние между вершинами двух сферических преломляющих поверхностей мало в сравнении с радиусами их кривизны), можно получить уравнение, которое связывает расстояния от оптического центра линзы до предмета (d)и до изображения (f) с показателем преломления материала линзы (n) и среды (no), в которой она находится, а также радиусами кривизны ее поверхностей R1 и R2 (рис.2).
Рисунок 2. Построение изображения в тонкой линзе
Это уравнение имеет вид:
В случае, когда предмет находится бесконечно далеко от линзы (d→∞), т.е. если лучи падают на линзу параллельно главной оптической оси, то получим:
Соответствующее этому случаю расстояние f=F называют фокусным расстоянием линзы.
Сравнивая формулы (1) и (2), окончательно получаем формулу тонкой линзы:
Эта формула пригодна для линз любой формы, только для собирающих линз фокусное расстояние F и величина f - положительны, а для рассеивающих F и f – отрицательны. В связи с этим собирающие линзы называют положительными и обозначают (например, в рецептах на очки) знаком (+), рассеивающие называют отрицательными и обозначают знаком (-). Величину, обратную фокусному расстоянию, называют оптической силой линзы:
где D измеряется в диоптриях (дптр). Диоптрия – это оптическая сила линзы с фокусным расстоянием 1 метр. Линейным увеличением линзы называют отношение размеров изображения (H) и предмета (h) и вычисляют по формуле:
откуда Подставляя значение f в формулу (3), получим:
Оптическая система, образованная несколькими сферическими поверхностями, отделяющих друг от друга оптически однородные среды, называется центрированной, если центры всех поверхностей лежат на одной прямой. Эту прямую называют оптической осью системы. Рассмотрим систему из двух линз, плотно прижатых друг к другу (рис.3).
Рисунок 3. Определение фокусного расстояния для системных линз
Допустим, что предмет А находится в фокусе первой линзы. Луч, вышедший из первой линзы, будет параллельным оптической оси и, следовательно, пройдет через фокус второй линзы. Рассматривая эту систему как одну линзу, можно написать, что
Этот результат верен и для более сложной системы тонких линз. Оптическая сила системы линз будет равна сумме оптических сил составных частей
В случаях двух отдельных линз с фокусными расстояниями F 1 и F2, расположенными вдоль одной и той же оси на расстоянии (а) друг от друга:
Яркость изображения, получаемого с помощью линзы, зависит от значений ее диаметра и оптической силы. Величину Светосила обуславливает яркость изображения, образуемого любой оптической системой, и зависит от плотности световой энергии, проходящей через линзу и дающей изображение предмета. Линза обеспечивает геометрически правильное и резкое изображение только при условии параксиальности (лучи идут под малыми углами к главной оптической оси) световых лучей и отсутствии дисперсии. При несоблюдении этих условий в изображении, которое дает линза, наблюдаются определенные недостатки и искажения. Основными из них являются: сферическая аберрация, кривизна поля и дисторсия, хроматическая аберрация, астигматизм наклонных пучков.
1. Сферическая аберрация. Это явление заключается в том, что лучи, удаленные от главной оптической оси, сильнее преломляются линзой, чем лучи, близкие к оси (параксиальные). Вследствие этого имеет место отклонение от гомоцентричности. На рисунке (4) показан пучок параллельных главной оптической оси лучей, которые, после преломления, практически не собираются в одной точке и дают расплывчатое изображение (пятно).
Рисунок 4. Ход лучей через собирающую линзу при сферической аберрации
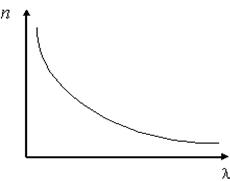
2. Хроматическая аберрация. Согласно формуле (2) фокус линзы зависит от показателя преломления n материала из которого изготовлена линза. В свою очередь показатель преломления линзы зависит от длины волны λ (явление дисперсии), т.е. n=f(λ). График этой зависимости имеет вид:
Рисунок 5. График зависимости показателя приломления линзы от длины волны
Проходя через линзу, белые лучи разлагаются на спектральные цвета так же, как при прохождении через призму. Лучи с малой длиной волны преломляются сильнее, чем лучи с большой длиной волны. Как следствие дисперсии, изображение белого источника света оказывается на экране окрашенным в спектральные цвета (хроматическаяаберрация). Левой части спектра соответствует фиолетовый цвет, а правой – красный цвет.
Рисунок 6. Ход лучей через собирающую линзу при хроматической аберрации
3. Астигматизм. Изображение прямого источника света, от которого падают на линзу сильно наклоненные к главной оптической оси лучи, получается не в одной плоскости в виде двух искривленных линий. Астигматизм имеет место в результате неодинакового преломления лучей, проходящих через линзу в различных меридианных плоскостях. Применяя соответствующим образом подобранные комбинации линз с недостатками, имеющими противоположный характер, можно добиться устранения их, что и делают на практике. В данной работе предлагается определить фокусное расстояние тонких собирающих и рассеивающих линз. Фокусное расстояние собирающей линзы можно определить, используя уравнение (3) и (6), если измерить соответствующие величины. Фокусное расстояние рассеивающей линзы можно определить следующими способами: 1. Зная фокусное расстояние собирающей линзы, составляют систему 2-х плотно сдвинутых линз (собирающей и рассеивающей), дающую действительное изображение. Определив опытным путем, фокусное расстояние полученной системы, вычисляют фокусное расстояние рассеивающей линзы из формулы:
2. Если на пути лучей, исходящих из точки А (рис. 5), поставить собирающую линзу, то лучи, преломляясь в ней, дадут изображение (точка В). При помещении рассеивающей линзы за собирающей, в результате рассеивания, действительное изображение переместится в положение С. Пользуясь принципом обратимости лучей (обратимы в данном случае точки С и А), можно положить, что точка С – есть предмет для рассеивающей линзы. Тогда ее изображение будет лежать в точке B. Следовательно, расстояние от рассеивающей линзы до точки С будет d, а от рассеивающей линзы до точки B – f. Измеряя эти расстояния и учитывая, что f – отрицательно, по формуле (3) рассчитывают фокусное расстояние рассеивающей линзы.
Рисунок 7. Измерение фокусного расстояния рассеивающей линзы Порядок выполнения работы
Упражнение 1. Определение фокусных расстояний собирающей линзы по измерениям d и f 1. На горизонтальной оптической скамье разместите осветитель, экран и линзу. Объект (предмет) в виде стрелки находится в передней стенке осветителя. 2. Перемещая линзу между экраном и предметом, добиваются четкого изображения предмета на экране. 3. По линейке отсчитывают расстояния d и f. (d – расстояние от предмета до линзы, f – расстояние от линзы до экрана (изображения)). 4. Меняя положение линзы и экрана, измеряют расстояния d и f не менее 3-х раз. 5. Измеряют линейкой диаметр (2r) линзы. 6. Результаты всех измерений заносят в таблицу 1.
Таблица 1 Результаты измерений и вычислений
7. Фокусное расстояние F, оптическую силу D, светосилу линзы L вычисляют по следующим формулам:
8. Расчет погрешностей производят по формулам:
Упражнение 2. Определение фокусного расстояния собирающей линзы по ее линейному увеличению 1. Располагают линзу между экраном и предметом так, чтобы получить сильно увеличенное резкое изображение. 2. Измеряют расстояние от предмета до линзы (d), величину предмета (h) и размер изображения (H). 3. Изменяя положение линзы, опыт повторяют 3 раза. 4. Результаты измерений заносят в таблицу 2. Таблица 2 Результаты измерений и вычислений
5. Фокусное расстояние F и оптическую силу линзы D вычисляют по формулам:
Упражнение 3. Определение фокусного расстояния рассеивающей линзы по принципу обратимости лучей в оптической системе, состоящей из собирающей и рассеивающей линз 1. Располагают осветитель, собирающую линзу, рассеивающую линзу и экран на оптической скамье и получают на экране четкое действительное изображение (см. рис.6). 2. Измеряют расстояние от экрана до центра рассеивающей линзы (d), заметив положение рассеивающей линзы. 3. Убирают рассеивающую линзу и, перемещая экран, добиваются на нем четкого изображения с помощью оставшейся собирающей линзы. 4. Измеряют расстояние от нового положения экрана до замеченного положения рассеивающей линзы.
Рисунок 8. Определение фокуса рассеивающей линзы
5. Результаты измерений занести в таблицу 3. 6. Опыт проделать 3 раза.
Таблица 3 Результаты измерений и вычислений
7. Рассчитываем фокусное расстояние F рассеивающей линзы по формуле:
Контрольные вопросы 1. Формулы тонкой линзы, оптической силы и светосилы линзы, линейное увеличение. 2. Методы определения фокусных расстояний и оптических сил линз. 3. Правила построения изображений, получаемых с помощью линз. 4. Недостатки линз (сферическая аберрация, хроматическая аберрация, астигматизм). 5. Глаз как оптическая система. 6. Дальнозоркость и близорукость. Исправление близорукости и дальнозоркости с помощью линз.
Список литературы основная литература 1. Козырев А.В. Курс лекций по физике / А. В. Козырев; Томск: ТУСУР, 2007. – 421с. 2. Детлаф А.А. Курс физики: Учебное пособие для вузов / А. А. Детлаф, Б. М. Яворский. – М.: Академия, 2007. – 719с. 3. Савельев И. В. Курс общей физики: учебное пособие для втузов: В 3 т. / И. В. Савельев. – СПб.: Лань, 2007 – 432 с. 4. Трофимова Т. И. Курс физики: учебное пособие для вузов / Т. И. Трофимова. – М.: Академия, 2010. – 557 с. 5. Антонов В.Ф. Физика и биофизика: курс лекций для студентов медицинских вузов / В.Ф. Антонов, А.В. Коржуев.- М.: Гэотар Медицина, 2004.- 192 с. дополнительная литература 6. Биофизика / Ю.А. Владимиров [и др.].- М.: Медицина, 1983.- 272 с. 7. Биофизика: учебник для студентов высших учебных заведений / В.Ф. Антонов [и др.]; под ред. В.Ф. Антонова.- М.: Гуманитарный издат. центр «ВЛАДОС», 2000.- 288 с. 8. Гмурман В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман.- М.: Высшая школа, 1999.- 479 с. 9. Грабовский Р.И. Курс физики / Р.И. Грабовский. - М.: Высшая школа, 1974. 10. Дунаев А.А. Основы теории вероятностей и математической статистики / А.А. Дунаев, В.А. Тупицын.- Рязань: РязГМУ, 2001. 11. Костылев В.А. Медицинская физика / В.А. Костылев.- М.: Медицина, 2008. 12. Ливенцев Н.М. Курс физики / Н.М. Ливенцев. - М.: Высшая школа, 1978. 13. Практикум по физике / В.А. Хитун [и др.].- М., 1972.- С. 50-65; 103-108. 14. Пустовалов А.П. Избранные вопросы медбиофизики: учебное пособие / А.П. Пустовалов.- Рязань: РязГМУ, 2002.- 123 с. 15. Ремизов А.Н. Курс физики / А.Н. Ремизов - М.: Высшая школа, 1998.- С. 103-104; 111-112. 16. Ремизов А.Н. Медицинская и биологическая физика / А.Н. Ремизов, А.Г. Максина, А.Я. Потапенко. - М.: Дрофа, 2003.- 560 с. 17. Ремизов А.Н. Медицинская и биологическая физика / А.Н. Ремизов.- М.: Высшая школа, 2000. 18. Ремизов А.Н. Медицинская и биологическая физика / А.Н. Ремизов.- М.: Высшая школа, 1987. 19. Руководство к лабораторным работам по медицинской и биологической физике / И.А. Эссаулова [и др.].- М., 1987.- С.198-203.
Содержание
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 937; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.014 с.) |



 ; или
; или 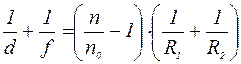 (1)
(1)
 (2)
(2) (3)
(3) ;(4)
;(4) ; (5)
; (5) .
.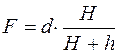 ; (6)
; (6)
 . Так как
. Так как  ,
,  , то
, то 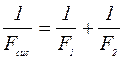 (7)
(7) . (8)
. (8) (9)
(9) называют относительным отверстием, а
называют относительным отверстием, а  - светосилой линзы, где 2r – диаметр линзы.
- светосилой линзы, где 2r – диаметр линзы.

 ; откуда
; откуда  (8);
(8);
 ;
;  ;
; 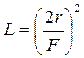
 ;
; ;
; – половина деления измерительной ленты.
– половина деления измерительной ленты. ;
; 



 по скорости звука в газе
по скорости звука в газе



