
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика вычислений инструментальных погрешностей прямых (непосредственных) измеренийСодержание книги
Поиск на нашем сайте Прямыми называются измерения, при которых результат измерения получается путем непосредственного сравнения измерения величины с эталоном или его эквивалентом, принятым за единицу измерения. X=n·[x], где n – число, целое или дробное, [x] – единица измерения. Погрешность измерения, выраженная в единицах измеряемой величины называется абсолютной погрешностью ∆X; численно она равна разности между результатом измерения Х и истинным значением Х0 измеряемой величины: ∆Х = Х - Х0. (1) Если абсолютная погрешность по модулю не превышает некоторого положительного числа ∆Xм, то это число называется максимальной абсолютной погрешностью: |Х – Х0| = |∆Х |≤ ∆Xм . (2) Относительной погрешностью называется отношение абсолютной погрешности к истинному значению измеряемой величины:
Аналогично максимальная относительная погрешность равна отношению максимальной абсолютной погрешности к истинному значению измеряемой величины:
Точность измерительных инструментов, приборов принято оценивать величиной приведенной погрешности, равной отношению максимальной абсолютной погрешности к верхнему пределу измерения для данного прибора (к пределу шкалы Xм):
Приведенная погрешность, выраженная в процентах, называется классом точности прибора. Всего ГОСТом установлено восемь классов точности для измерения электрических величин: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Класс точности проставляется по шкале прибора. По известному классу точности можно найти максимальную абсолютную погрешность отдельного измерения:
Например, вольтметр с классом точности 1,0 и шкалой до 30 В измеряет приложенное к нему напряжение с максимальной абсолютной погрешностью:
Это означает, что если результат измерения, например, 15,2 В, то истинное значение отличается от 15,2 В не больше, чем на 0,3 В, т.е.
Если на приборе не указан класс точности, то его максимальная абсолютная погрешность принимается равной половине цены деления шкалы. В некоторых случаях, например, при измерении времени секундомером, за величину максимальной абсолютной погрешности принимается целое деление (например, 0,02 с). В приборах с выдачей результатов измерения непосредственно на цифровом индикаторе за максимальную погрешность часто принимается единица младшего разряда. В общем случае результаты прямых измерений содержат систематические, случайные и грубые погрешности. Систематические погрешности могут быть устранены либо в процессе измерения, либо учтены введением поправок в результаты. Поэтому условимся считать, что результаты прямых измерений содержат только случайные и грубые погрешности.
|
||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.009 с.) |

 . (3)
. (3)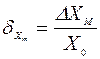 . (4)
. (4) . (5)
. (5) . (6)
. (6) .
.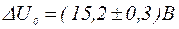 или в другой записи
или в другой записи  .
.


