
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 9 Плоские и сферические зеркала, системы плоских зеркалСодержание книги
Поиск на нашем сайте
Плоское зеркало — оптическая деталь с плоской отражающей поверхностью. Чтобы построить изображение точки в плоском зеркале, достаточно продолжить отраженные лучи до их пересечения или отложить от зеркальной плоскости в противоположную сторону по перпендикуляру расстояние S', равное расстоянию s до предмета (рис. 9). Изображение в плоском зеркале является мнимым, равным предмету по размерам, одинаковым по форме, цвету и положению, симметрично расположенным относительно зеркальной поверхности, но не совместимым с предметом при любых поворотах и перемещениях в одной плоскости. Зеркальное изображение может быть только наложено на предмет. Зеркальное изображение еще называется полуобращенным. Изображение линии и любого тела в плоском зеркале суть изображение семейства отдельных точек предмета. Оптическая сила плоского зеркала равна нулю, поэтому при расчетах оптических систем плоские зеркала не принимаются во внимание. В геодезических приборах широко применяются или отдель Угол отклонения луча от первоначального направления
При повороте зеркала на угол а(альфа) угол отклонения луча изменится на 2 а(альфа), т. е.
Два параллельно установленных зеркала на рис. 12 смещают луч параллельно самому себе (e1 =e2') на величину где О\02 = d/соse' d — расстояние между зеркалами, Два зеркала, расположенные под углом а(альфа) изменяют направление луча на угол
Если а=45°, то система двух зеркал является эккером — прибором для построения прямых углов
Вопрос№10 Отражательные призмы Призма — оптическая деталь с плоскими поверхностями, образующими между собой двугранные углы. Различают призмы: ---преломляющие (в том числе оптические клинья), ---спектральные, ---поляризационные --- отражательные. Отражательные призмы отличаются тем, что угол падения любого луча на входную грань равен углу преломления этого луча на выходной грани. Как правило, это призмы полного внутреннего отражения. Важной характеристикой отражательных призм является длина хода луча в призме. Отношение длины хода луча в призме к диаметру отверстия пучка лучей называется коэффициентом призмы. Для отражательной призмы должно выполняться условие: призма, если ее разверткой является плоскопараллельная пластинка, в параллельном пучке лучей не должна давать хроматизма.
Призмы, или призменные отражательные системы, должны проверяться на возможность появления вредных (паразитных) отражений. Паразитных изображений можно избежать, если полный размер призмы не превышает требуемого светового размера, или путем применения специальных шторок.
Вопрос №11 Плоскопораллельная пластинка, оптический клин. Рассматривая плоскость как частный случай сферической поверхности из уравнения нулевого инварианта Аббе для луча, преломленного одной плоскостью 1/s = nls', откуда расстояние до изображения получится s' = sn Плоскопараллельная пластинка — оптическая деталь, ограниченная параллельными плоскостями
Отношение расстояния до изображения и до предмета равно постоянной величине для данных двух сред s'/s = n. В геодезических приборах распространенным является случай преломления луча двумя плоскими поверхностями в виде плоскопараллельной пластинки. Преломляясь в плоскопараллельной пластинке, луч смещается на величину h параллельно самому себе. Величина h определяется как h = ABsin(e — e'),
При толщине пластинки из стекла, равной 20 мм, величину смещения можно вычислять до 0,01 мм по любой формуле, если угол падения не превышает 10°. При углах больше 25°можно вычислять с указанной точностью только по точным формулам. Смещение луча h, вычисленное по приближенной формуле, прямо пропорционально толщине пластинки и углу падения е. Это свойство плоскопараллельных пластинок используется в оптических микрометрах при точных измерениях долей делений шкал. В геодезических приборах плоскопараллельные пластинки применяются
Оптическая сила плоскопараллельных пластинок равна нулю (Ф = 0), значит они являются телескопическими системами, обладающими всеми свойствами телескопических систем. Оптический клин. Луч ABCD (рис. 35) проходит через призму с преломляющим углом В геодезических приборах находят применение призмы с малыми преломляющими углами Оптические клинья применяются в оптических микрометрах геодезических приборов и в дальномерах двойного изображения. Дисперсия клина равна
Дисперсия клина устраняется изготовлением ахроматического клина, состоящего из двух стекол (флинт и крон), имеющих разные показатели преломления. Пучок лучей, выходящий из склеенного клина, будет снова белым, о чем свидетельствует параллельность лучей, вышедших из клина. Клинья склеиваются так, чтобы преломляющие углы были противоположны, а преломляющие ребра — параллельны. Вопрос №12 Преломление луча сферической поверхностью. Наибольшее распространение в геодезических приборах имеют детали со сферическими преломляющими поверхностями. Простейшей оптической центрированной системой является оптическая система с одной сферической преломляющей поверхностью. На рисунке сферическая поверхность с вершиной О и радиусом r разделяет две оптически прозрачные среды с показателями преломления п и п'. Центр сферы — точка С и оптическая ось — ОС. На расстоянии s от поверхности раздела на оптической оси выберем точку А (предмет). Из этой точки проведем произвольный луч AM (в области параксиального пучка, когда
Формула носит название основной формулы параксиальной оптики;
Ооптическая сила Ф системы через ее фокусное расстояние - основное уравнение преломления луча
Придадим формуле Гаусса другой вид. -s=-f-z,
Сферическая преломляющая поверхность характеризуется также угловым увеличением
Зависимость между угловым и линейным увеличениями
Для оптической системы в воздухе или в пустоте имеем
Продольное увеличение системы определяют по формуле
Продольное увеличение систем связано с глубиной резкого изображения оптической системы вдоль оси. Линейное увеличение β систем характеризует увеличение предмета в фокальной плоскости, рассматриваемое окуляром. Видимое или окулярное увеличение Г есть отношение двух изображений на сетчатке: изображения предмета, рассматриваемого через оптическую систему, к изображению того же предмета, рассматриваемого невооруженным глазом. Видимое увеличение можно определить как отношение тангенсов углов, под которыми предмет рассматривается через оптическую систему и невооруженным глазом
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.42.25 (0.008 с.) |






 В геодезических приборах применяют одинарные отражательные призмы, составные призмы и системы призм. Призмы с четным числом отражательных граней дают конгруэнтное изображение предмета, с нечетными — неконгруэнтиое (зеркальное). Исключением является призма-«крыша». Принято единое обозначение отражательных призм. Каждую призму обозначают двумя буквами и числом градусов в угле, на который отклоняется луч после прохождения через призму. Первая буква указывает на число отражающих граней: А — одна, Б — две, В — три. Вторая буква характеризует конструкцию призмы: Р — равнобедренная, П — пента, У — по-лупента, С — ромбическая, Л—Лемана, М—дальномерного типа. Крышу условно считают за одну грань и обозначают индексом «К». Каждую составную призму (систему призм) обозначают начальной буквой ее названия и числом градусов в угле, на который отклоняется луч. Например, А — 0° — призма Аббе, угол отклонения 0°, П— 0° — призма Пехана, угол отклонения 0°.
В геодезических приборах применяют одинарные отражательные призмы, составные призмы и системы призм. Призмы с четным числом отражательных граней дают конгруэнтное изображение предмета, с нечетными — неконгруэнтиое (зеркальное). Исключением является призма-«крыша». Принято единое обозначение отражательных призм. Каждую призму обозначают двумя буквами и числом градусов в угле, на который отклоняется луч после прохождения через призму. Первая буква указывает на число отражающих граней: А — одна, Б — две, В — три. Вторая буква характеризует конструкцию призмы: Р — равнобедренная, П — пента, У — по-лупента, С — ромбическая, Л—Лемана, М—дальномерного типа. Крышу условно считают за одну грань и обозначают индексом «К». Каждую составную призму (систему призм) обозначают начальной буквой ее названия и числом градусов в угле, на который отклоняется луч. Например, А — 0° — призма Аббе, угол отклонения 0°, П— 0° — призма Пехана, угол отклонения 0°. Призмы (а, б, в) рис 15дают полуобращенное (зеркальное) изображение. Составные призмы, рис. 16, дают зеркальные изображения. Отражательные призмы применяются для изменения направления оптической оси системы (в нивелирах с компенсаторами, номограммных тахеометрах и кипрегелях); оборачивания изображения (в зрительных трубах с прямым изображением); удлинения габаритного хода луча; разделения пучков лучей и в других случаях, наряду с системами плоских зеркал.
Призмы (а, б, в) рис 15дают полуобращенное (зеркальное) изображение. Составные призмы, рис. 16, дают зеркальные изображения. Отражательные призмы применяются для изменения направления оптической оси системы (в нивелирах с компенсаторами, номограммных тахеометрах и кипрегелях); оборачивания изображения (в зрительных трубах с прямым изображением); удлинения габаритного хода луча; разделения пучков лучей и в других случаях, наряду с системами плоских зеркал.
 В большинстве случаев при расчетах можно воспользоваться приближенными формулами
В большинстве случаев при расчетах можно воспользоваться приближенными формулами также в качестве шкал, лимбов, сеток, защитных стекол и светофильтров.
также в качестве шкал, лимбов, сеток, защитных стекол и светофильтров. и показателем преломления п под углом падения
и показателем преломления п под углом падения  .
. , называемые оптическими клиньями (рис. 36).* Преломляющая призма — оптическая деталь с плоскими преломляющими поверхностями, расположенными под некоторыми углами друг к другу. Оптическому клину присущи свойства гомоцентричности пучка и стигматичности изображения. Изображение точки А, рассматриваемой через оптический клин (см. рис. 36), получится в точке А', т. е. смещенным на величину
, называемые оптическими клиньями (рис. 36).* Преломляющая призма — оптическая деталь с плоскими преломляющими поверхностями, расположенными под некоторыми углами друг к другу. Оптическому клину присущи свойства гомоцентричности пучка и стигматичности изображения. Изображение точки А, рассматриваемой через оптический клин (см. рис. 36), получится в точке А', т. е. смещенным на величину

 до границы раздела двух сред.
до границы раздела двух сред. На рисунке луч из точки А в точку М идет под малым углом
На рисунке луч из точки А в точку М идет под малым углом  к оптической оси. Лучи падающий и преломленный образуют с нормалью МС (радиусом кривизны сферы) соответственно малые углы падения
к оптической оси. Лучи падающий и преломленный образуют с нормалью МС (радиусом кривизны сферы) соответственно малые углы падения  и преломления.
и преломления.  Высота точки падения М над оптической осью равна h. /По закону преломления при малых углах имеем
Высота точки падения М над оптической осью равна h. /По закону преломления при малых углах имеем Для треуг.АМС угол
Для треуг.АМС угол  является внешним и равен сумме внут ренних
является внешним и равен сумме внут ренних  углов, не смежных с ним,
углов, не смежных с ним, 



 Для параксиального пучка s' инвариант Гюйгенса — Гельмгольца
Для параксиального пучка s' инвариант Гюйгенса — Гельмгольца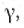 отношением углов
отношением углов  и
и  образованных преломленным и падающим параксиальными лучами с оптической осью,
образованных преломленным и падающим параксиальными лучами с оптической осью,


 где zи z ' — сопряженные отрезки на оси
где zи z ' — сопряженные отрезки на оси




