
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основное уравнение измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ТЕМА 1. ОСНОВНЫЕ ПОНЯТИЯ В ОБЛАСТИ МЕТРОЛОГИИ 1.1 Основные термины и определения в области метрологии
Основные термины и определения в области метрологии регламентируются рекомендациями по межгосударственной стандартизации РМГ 29 – 99 «ГСИ. Метрология. Основные термины и определения». Метрология – наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности. Метрология включает в себя три раздела: 1) теоретическая (фундаментальная) метрология – раздел метрологии, предметом которого является разработка фундаментальных основ метрологии; 2) законодательная метрология – раздел метрологии, предметом которого является установление обязательных технических и юридических требований по применению единиц физических величин, эталонов, методов и средств измерений, направленных на обеспечение единства и необходимости точности измерений в интересах общества; 3) практическая (прикладная) метрология – раздел метрологии, предметом которого являются вопросы практического применения разработок теоретической метрологии и положений законодательной метрологии. Объектами метрологии являются физические величины, их единицы, средства измерений, эталоны, методики выполнения измерений. Традиционным объектом метрологии является физическая величина – одно из свойств физического объекта (физической системы, явления или процесса), общее в качественном отношении для многих физических объектов, но в количественном отношении индивидуальное для каждого из них. Единство измерений – состояние измерений, характеризующееся тем, что их результаты выражаются в узаконенных единицах, размеры которых в установленных пределах равны размерам единиц, воспроизводимых первичными эталонами, а погрешности результатов измерений известны и с заданной вероятностью не выходят за установленные пределы.
Основное уравнение измерений
Для установления различия в количественном содержании отображаемого данной физической величиной свойства изучаемых объектов (явлений, процессов) введено понятие «размер физической величины» – количественная определенность физической величины, присущая конкретному материальному объекту, системе, явлению или процессу. Истинный размер физической величины является объективной реальностью, не зависящей от того, измеряют соответствующую характеристику свойства объекта или нет. Количественной оценкой физической величины является значение физической величины – выражение размера физической величины в виде некоторого числа принятых для нее единиц. Числовое значение физической величины – отвлеченное число, входящее в значение величины. Данные определения формализовано выражаются в виде:
X = q [X], (1.1)
где Х – физическая величина; q – числовое значение величины Х; [Х] – единица измерения величины Х. Например, за единицу измерения напряжения электрического тока принят 1 В. Тогда значение напряжения электрической сети U = q [U] = 220 [1B] = 220B. Здесь числовое значение q = 220. Но если за единицу напряжения принять [1 кВ], то U = q [U] = 0,22 [1 кВ] = 0,22 кВ, т. е. числовое значение q = 0,22, а размер величины не изменяется. Уравнение (2.1) называется основным уравнением измерений, показывающим, что числовое значение величины зависит от размера принятой единицы измерения. Шкалы измерений
Упорядоченная совокупность значений физической величины, служащая исходной основой для измерений данной величины, называется шкалой физической величины. Все виды шкал измерений разделяются на следующие: 1) шкалы наименований характеризуются только отношением эквивалентности различных качественных проявлений свойства. Эти шкалы не имеют нуля и единицы измерений, в них отсутствуют отношения сопоставления типа «больше – меньше». Пример шкал наименований: шкалы цветов, представляемые в виде атласов цветов; 2) шкалы порядка свойства величин описывают как отношением эквивалентности, так и отношением порядка по возрастанию или убыванию количественного проявления свойства. В этих шкалах может в ряде случаев иметься нуль (нулевая отметка), но принципиальным для них является отсутствие единицы измерения, поскольку невозможно установить, в какое число раз больше или меньше проявляется свойство величины. Примеры шкал порядка: шкалы чисел твердости, баллов силы ветра, землетрясений; 3) шкалы интервалов (разностей) описывают свойства величин не только с помощью отношений эквивалентности и порядка, но также и с применением суммирования и пропорциональности интервалов (разностей) между количественными проявлениями свойства. Шкалы разностей могут иметь условные нули и единицы измерений, установленные по согласованию. Так, по шкале интервалов времени их можно суммировать (вычитать) и сравнивать, во сколько раз один интервал больше (меньше) другого; 4) шкалы отношений описывают свойства величин, для множеств количественных проявлений которых применимы логические отношения эквивалентности, порядка и пропорциональности, а для некоторых шкал также отношение суммирования. В шкалах отношений существует естественный нуль и по согласованию устанавливается единица измерения. Примерами шкалы отношений являются шкалы массы и термодинамической температуры; 5) абсолютные шкалы, кроме всех признаков шкал отношений, обладают дополнительным признаком: в них естественно, однозначно присутствует определение единицы измерения. Абсолютные шкалы присущи относительным единицам таким, как коэффициенты усиления, ослабления, полезного действия и др. Ряду абсолютных шкал, например, коэффициентов полезного действия присущи границы, заключенные между нулем и единицей. Шкалы наименований и порядка относятся к условным (неметрическим) шкалам – шкала физической величины, исходные значения которой выражены в условных единицах. Шкалы интервалов, отношений и абсолютные называются метрическими.
ТЕМА 2. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ И ИХ ЕДИНИЦЫ Физические величины
Физические величины разделяют: 1) основные – физические величины, входящие в систему величин и условно принятые в качестве независимых от других величин этой системы (пример – масса m); 2) производные – физические величины, входящие в систему величин и определяемые через основные величины этой системы (пример – сила F = m·a). К основным величинам относятся: длина, масса, время, сила электрического тока, термодинамическая температура, количество вещества, сила света. К производным – такие, как сила, частота и т.д.
Принципы измерений
Принцип измерений – это физическое явление или эффект, положенное в основу измерений. Рассмотрим лишь несколько широко распространенных эффектов. 1. Пьезоэлектрический эффект заключается в возникновении ЭДС на поверхности (гранях) некоторых кристаллов (кварц, турмалин, искусственные пьезоэлектрические материалы – пьезокерамики и др.) под действием внешних сил (сжатие, растяжение). Наибольшее применение для измерений нашли кварц и пьезокерамики (например, титанат бария), обладающие достаточно высокой механической прочностью и температурной стабильностью (кварц до температуры примерно 200 °С, пьезокерамика – до 115 °С). Пьезоэлектрический эффект обратим: ЭДС, приложенная к пьезоэлектрическому кристаллу, вызывает механические напряжения на их поверхности. 2. Термоэлектрический эффект широко применяется при измерениях температуры, причем используются две основных разновидности способов использования этого эффекта. В первом используется свойство изменения электрического сопротивления металлов и полупроводников при изменении температуры. Из металлов часто применяются медь (для обычных измерений) и платина (для высокоточных измерений). Соответствующий измерительный преобразователь называется терморезистором. Чувствительные элементы полупроводникового преобразователя – термистора – изготавливаются из окислов различных металлов. С увеличением температуры сопротивление термистора уменьшается, в то время как у терморезистора – возрастает. Зависимость изменения сопротивления термисторов при изменении температуры существенно нелинейна, у медных терморезисторов – линейна, у платиновых аппроксимируется квадратным трехчленом. Платиновые терморезисторы позоляют измерять температуру в пределах от минус 200 до + 1000 °С. Другим способом использования термоэлектрического эффекта является возникновение термо-ЭДС в замкнутом контуре, состоящем из двух разнородных проводников (или полупроводников), соединенных (спаянных) между собой на одном конце, а на другом подключенным к измерителю ЭДС, при различии температуры в месте спая и в месте соединения с измерителем. Соответствующие соединения двух разнородных проводников (полупроводников) называются термопарами. Широко используются для термопар хромель, копель, константан, платина и др. Термопары позволяют измерять температуру в широком диапазоне (от минус 200 до + 2800 °С). Например, пара хромель-константан позволяет измерять температуру до + 700 °С, а пара вольфрам-рений – до + 2800 °С. При этом приходится применять чувствительные измерители ЭДС, так как величина термо-ЭДС составляет от значений примерно 10 до 80 мкВ/°С. 3. Фотоэлектрический эффект. Для целей измерений используется внешний и внутренний фотоэффекты. Внешний фотоэффект возникает в вакуумированном баллоне, имеющем анод и фотокатод. При освещении фотокатода в нем под влиянием фотонов света эмитируются электроны. В случае наличия между анодом и фотокатодом электрического напряжения эмитируемые фотокатодом электроны образуют электрический ток, называемый фототоком. Таким образом, происходит преобразование световой энергии в электрическую. Описанный преобразователь называется фотоэлементом. Существуют также газонаполненные фотоэлементы. Внутренний фотоэффект возникает при освещении слоя между некоторыми полупроводниками и металлами. В этом слое возбуждается ЭДС. У ряда полупроводников под влиянием светового излучения изменяется электрическое сопротивление. Иногда этот эффект называется фоторезистивным, а соответствующие устройства – фоторезисторами. «Темновое» (при отсутствии освещения) сопротивление фоторезистора достаточно большое (например, 108 Ом). При освещении оно может уменьшиться до 105 Ом. Фоторезисторы обладают высокой чувствительностью, существенно превышающей чувствительность фотоэлементов. В качестве фоточувствительного материала применяют сернистый кадмий, сернистый свинец, кремний и др.
Методы измерений Метод измерений – прием или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализованным принципом измерений. Методика выполнения измерений – установленная совокупность операций и правил при измерении, выполнение которых обеспечивает получение результатов измерений с гарантированной точностью в соответствии с принятым методом. Методы измерений делятся: 1) метод непосредственной оценки – метод измерений, при котором значение величины определяют непосредственно по показывающему средству измерений; 2) метод сравнения с мерой – метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой (пример: измерение массы на рычажных весах с уравновешиванием гирями (мерами массы с известным значением)). Методы сравнения реализуются следующими способами: - дифференциальный метод измерений – метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами. Точность этого метода может быть высокой и определяется точностью величины, воспроизводимой мерой. Характерным примером дифференциального метода, иногда называемого методом неполного уравновешивания, является приведенный на рисунке 3.1. Вольтметр V включается с помощью переключателя П в цепь с измеряемым сопротивлением rx или в цепь с регулируемым потенциометром (мерой) r0. При достижении одинаковых показаний вольтметра (rx = r0) регистрируется искомое значение rx; - нулевой метод измерений – метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля. Характерным примером нулевого метода является измерение активного сопротивления мостом постоянного тока (рисунок 3.2).

Мостовая схема оказывается полностью уравновешенной (гальванометр G показывает нуль), когда выполняется следующее условие: rxr2 = r1r3. Таким образом, при полном уравновешивании искомая величина rx = r1r3/r2; - метод измерений замещением – метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины. Пример: взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов (метод Борда); - метод совпадений – метод сравнения с мерой, в котором разность между измеряемой величиной и известной величиной, воспроизводимой мерой измеряют, используя совпадения отметок шкал. Пример: измерение с помощью штангенциркуля.
ТЕМА 4. СРЕДСТВА ИЗМЕРЕНИЙ Основные понятия о средствах измерений
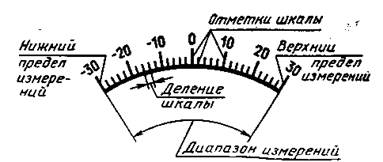
Средство измерений – техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени. Измерительное устройство – часть измерительного прибора (установки или системы), связанная с измерительным сигналом и имеющая обособленную конструкцию и назначение. Показывающее устройство средства измерений – совокупность элементов средства измерений, которые обеспечивают визуальное восприятие значений измеряемой величины или связанных с ней величин. Указатель средства измерений – часть показывающего устройства, положение которой относительно отметок шкалы определяет измерительное устройство показания средства измерений. Шкала средства измерений – часть показывающего устройства средства измерений, представляющая собой упорядоченный ряд отметок вместе со связанной с ними нумерацией (рисунок 4.1).
Рисунок 4.1 – Шкала средства измерений
Отметки на шкалах могут быть нанесены равномерно или неравномерно. В связи с этим можно выделить следующие виды шкал: 1) равномерная – шкала, длина делений которой не изменяется (рисунок 4.1); 2) практически равномерная – шкала, длина делений которой отличается друг от друга не более чем на 30 % и имеет постоянную цену делений; 3) неравномерная – шкала, длина делений которой отличается друг от друга более чем на 30 % и (или) имеет непостоянную цену делений; 4) существенно неравномерная – шкала с сужающимися делениями, для которой значение выходного сигнала, соответствующее полусумме верхнего и нижнего пределов диапазона изменений входного (выходного) сигнала, находится в интервале между 65 и 100 % длины шкалы, соответствующей диапазону изменений входного (выходного) сигнала; 5) степенная – шкала с расширяющимися или сужающимися делениями, отличная от шкал, указанных выше. Деление шкалы – промежуток между двумя соседними отметками шкалы средства измерений (рисунок 4.1). Длина деления шкалы – расстояние между осями (или центрами) двух соседних отметок шкалы, измеренное вдоль воображаемой линии, проходящей через середины самых коротких отметок шкалы. Цена деления шкалы – разность значения величины, соответствующих двум соседним отметкам шкалы средства измерений. Диапазон измерений средства измерений – область значений величины, в пределах которой нормированы допускаемые пределы погрешности средства измерений (рисунок 4.1). Значения величины, ограничивающие диапазон измерений снизу и сверху (слева и справа) называют соответственно нижним и верхним пределами измерений (рисунок 4.1).
ТЕМА 5. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ПОГРЕШНОСТЕЙ Определение погрешности
Качество средств и результатов измерений принято характеризовать, указывая их погрешности. Введение понятия "погрешность" требует определения и четкого разграничения трех понятий: 1) истинное значение физической величины – значение физической величины, которое идеальным образом характеризует в качественном и количественном отношении соответствующую физическую величину (истинное значение величины неизвестно, его применяют только в теоретических исследованиях. На практике используют действительное значение величины); 2) действительное значение физической величины – значение физической величены, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него; 3) результат измерения физической величины – значение величины, полученное путем ее измерения. Понятие "погрешность" – одно из центральных в метрологии, где используются два понятия: 1) погрешность результата измерения (Δхизм) – отклонение результата измерения (хизм) от истинного (действительного) значения измеряемой величины (хист(д)):
Δхизм = хизм – хист(д). (5.1) Она указывает границы неопределенности значения измеряемой величины; 2) погрешность средства измерений – разность между показанием средства измерений и истинным (действительным) значением измеряемой физической величины. Она характеризует точность результатов измерений, проводимых данным средством. Эти два понятия во многом близки друг к другу и классифицируются по одинаковым признакам. К основным источникам возникновения погрешностей следует отнести примененного метода измерений; примененного средства измерения; условий проведения измерений; способу обработки результатов измерений; квалификации операторов и др.
Классификация погрешностей
Погрешности классифицируются по ряду признаков. Признак 1. По форме представления погрешности разделяются: 1) абсолютная погрешность Δ – погрешность измерения, выраженная в единицах измеряемой величины:
Δ = хизм – хист(д); (5.2)
2) относительная погрешность δ – погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины:
3) приведенная погрешность – относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона (нормирующее значение хн):
Нормирующее значение в зависимости от типа измерительного прибора, а также от вида его шкалы определяется следующими способами: 1) для средств измерений с равномерной, практически равномерной или степенной шкалой ХN следует устанавливать равным большему из пределов измерений:
или равным большему из модулей пределов измерений:
2) аналогично вышеуказанному случаю устанавливается ХN для измерительных преобразователей, если нулевое значение входного (выходного) сигнала находится на краю или вне диапазона измерений; 3) для электроизмерительных приборов с равномерной, практически равномерной или степенной шкалой и нулевой отметкой внутри диапазона измерений ХN допускается устанавливать равным сумме модулей пределов измерений:
4) для средств измерений физической величины, для которой принята шкала с условным нулем, ХN устанавливают равным модулю разности пределов измерений:
5) для средств измерений с установленным номинальным значением ХN устанавливают равным этому номинальному значению: ХN = хном (например, для мер); 6) для измерительных приборов с существенно неравномерной шкалой ХN устанавливают равным всей длине шкалы или ее части, соответствующей диапазону измерений. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах шкалы. Признак 2. По характеру изменения результатов при повторных измерениях погрешности разделяются: 1) систематическая погрешность – составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Постоянные систематические погрешности свидетельствуют, прежде всего, о высоких или недостаточных показателях метрологической надежности применяемого средства измерения и могут быть устранены (учтены) предусмотренными аппаратурными методами коррекции или введением поправок в результаты измерений. Одной из распространенных систематических погрешностей является погрешность градуировки (погрешность нанесения делений на шкалу измерительного прибора). Данная погрешность легко выявляется, составляется таблица поправок, которая используется при определении результата измерений. Закономерно изменяющиеся систематические погрешности, возрастающие со временем эксплуатации средства измерения, как правило, квазимонотонно, называются прогрессирующими систематическими погрешностями. Они вызываются процессами старения узлов (комплектующих изделий) средства измерения (микросхем, резисторов, конденсаторов, и др.). Вследствие этого контролируемые и неконтролируемые параметры (характеристики) измерительных приборов изменяются и соответственно возрастают инструментальные погрешности средств измерений, по рассматриваемой классификационной группе относящиеся к систематическим. Старению подвержены и меры, например, концевые меры длины, гири. Это происходит из-за постепенного стирания поверхностей, окисления и других процессов. В некоторых случаях систематические погрешности могут изменяться периодически, в связи с чем они называются периодическими. Если систематическая погрешность постоянна для данного экземпляра средства измерения, то для большого числа средств измерений данного типа эта погрешность может более или менее отличаться случайным образом. Поэтому систематическая погрешность «ансамбля» приборов данного типа обычно рассматривается как случайная. Систематические погрешности наиболее просто выявить путем сопоставления результатов измерений физической величины, проведенных с помощью исследуемого средства измерения, и с помощью однородного – более точного; 2) случайная погрешность – составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины. В процессе любого измерения присутствуют многочисленные влияющие величины, учесть которые практически невозможно, но их совместное воздействие (случайная комбинация воздействий) сказывается на получении результатов измерений, а следовательно, и на погрешности измерений. В связи с этим до проведения измерений предсказать значение случайной погрешности невозможно. Случайная погрешность в отличие от систематической не может быть исключена из результата измерения, но ее влияние можно уменьшить с помощью многократных измерений искомой величины с последующим определением характеристик случайной погрешности методами математической статистики. Полученные при многократных измерениях результаты рассматриваются как случайные величины. К случайным погрешностям в большинстве случаев относятся и так называемые промахи (грубые погрешности) – погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Источником грубой погрешности чаще всего является неправильный отсчет показаний прибора. Иногда они могут возникать при скачкообразном изменении условий измерений (например, внезапное изменение напряжения питающей сети). При статистическом анализе промахи могут быть выявлены и соответствующие им результаты исключены. Признак 3. По причине возникновения погрешности разделяются: 1) инструментальная погрешность – составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений. Данный вид погрешности определяется несовершенством средств измерений, неидеальной реализацией принципа действия, конструктивно-технологическими особенностями средства измерения и влиянием внешних условий. К инструментальным погрешностям обычно относят также помехи на входе средства измерения, вызываемые его подключением к объекту измерений. Инструментальная погрешность является одной из наиболее ощутимых составляющих погрешности, причем некоторые из инструментальных погрешностей являются систематическими, другие – случайными (например, за счет нестабильности параметров комплектующих изделий, входящих в измерительные цепи прибора); 2) погрешность метода измерений (методическая погрешность) – составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений. Также к методическим относят погрешности, обусловленные несовершенством, недостатками примененного в средстве измерения метода измерений и упрощений при построении конструкции средства измерения, в том числе математических зависимостей; 3) субъективная погрешность – составляющая систематической погрешности измерений, обусловленная индивидуальными особенностями оператора (степень внимательности, сосредоточенности, подготовленности). Эти погрешности практически отсутствуют при использовании автоматических или автоматизированных средств измерений; Признак 4. По условиям проведения измерений погрешности средств измерений разделяются: 1) основная погрешность – погрешность средства измерений, применяемого в нормальных условиях. Нормальные условия устанавливаются нормативно-техническими документами на виды средств измерений или отдельные их типы. Установление условий применения и особенно нормальных условий является весьма важным для обеспечения единообразия метрологических характеристик средств измерений. В противном случае погрешности средств измерений одного и того же типа, отнесенные к различным внешним условиям применения, будут несопоставимы. Выделение основной погрешности, соответствующей некоторым стандартным условиям применения, является одним из важных факторов обеспечения единства измерений. В большинстве нормативно-технических документов на средства измерений к нормальным относятся следующие внешние условия: - температура окружающей среды 293 К ± 5 К; - относительная влажность 65 % ± 15 %; - атмосферное давление 101,3 кПа ± 4 кПа (750 мм рт. ст. ± 30 мм рт. ст.); - напряжение питающей электрической сети (для электрических и других средств измерений, имеющих электрические цепи) 220 В ± 2 % с частотой 50 Гц. Для некоторых средств измерений допускается отклонение значений влияющих условий от нормальных. В этом случае кроме нормальных в техническом паспорте, техническом описании и других документах на тип средства измерений указываются рабочие условия, в пределах которых допускается эксплуатировать средства измерений с гарантированными метрологическими характеристиками (например, термопары могут эксплуатироваться при температурах от – 200 ºС до + 2800 ºС; 2) дополнительная погрешность – составляющая погрешности средства измерений, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения или вследствие ее выхода за пределы нормальной области значений. Принято различать дополнительные погрешности по отдельным влияющим величинам (дополнительная температурная погрешность, дополнительная, погрешность за счет изменения атмосферного давления и т. д.). Как правило, наиболее значимой влияющей величиной является температура окружающей среды. Признак 5. По характеру изменения физической величины погрешности средства измерения разделяются: 1) статическая погрешность средства измерений – погрешность средства измерений, применяемого при измерении физической величины, принимаемой за неизменную. 2) динамическая погрешность средства измерений – погрешность средства измерений, возникающая при измерении изменяющейся (в процессе измерений) физической величины Проведенная классификация погрешностей измерений не является формальностью, с помощью которой можно детализировать их с тех или иных сторон представления, различия и причинности. Данная классификация широко используется при изучении погрешностей, в том числе с помощью воспроизведения (имитации) условий, при которых в процессе производства измерений проявляются соответствующие погрешности. Кроме этого, в большинстве случаев проведения экспериментов, когда результат измерений необходимо знать с погрешностью, не превышающей заданную, приходится учитывать общую погрешность измерений путем суммирования отдельных ее составляющих, различающихся по содержательным и количественным признакам.
5.3 Зависимость изменения погрешностей при различных формах их представления от значения измеряемой величины
По зависимости изменения значений погрешности от значения измеряемой величины абсолютная погрешность делится: 1) аддитивная (Δ = ± а):
Рисунок 5.1
В этом случае абсолютная погрешность не зависит от значения измеряемой величины и значение погрешности не изменяется; 2) мультипликативная (Δ = ± bх):
Рисунок 5.2
В этом случае абсолютная погрешность изменяется прямопропорционально изменению значения измеряемой величины; 3) смешанная, т.е. абсолютная погрешность имеет и аддитивную и мультипликативную составляющие (Δ = ± a + bx): В этом случае абсолютная погрешность имеет аддитивную составляющую на входе средства измерения, которая при изменении значения измеряемой величины также изменяется вследствие наличия мультипликативной составляющей. Рассмотренные выше случаи относятся к абсолютным погрешностям, имеющим линейную зависимость от изменения измеряемой величины. Если зависимость носит нелинейный характер, то такие погрешности называются нелинейными.
Рисунок 5.3
Изменение относительной погрешности в зависимости от изменения измеряемой величины связано с изменение абсолютной погрешности: 1) относительная погрешность определяется аддитивной абсолютной погрешностью (Δ = а; δ = Δ / х = а / х):
Рисунок 5.4
2) относительная погрешность определяется мультипликативной абсолютной погрешностью (Δ = bx; δ = Δ / х = b):
Рисунок 5.5
2) относительная погрешность определяется смешанной абсолютной погрешностью (Δ = а + bx; δ = Δ / х = b + а / х):
Рисунок 5.6
Характер изменения приведенной погрешности γ повторяет рассмотренные случаи изменения абсолютной погрешности, т.к. γ = Δ / хN, где хN – постоянная величина. В данном случае изменяется лишь масштаб зависимостей.
Понятие о ГМКиН
ГМКиН – деятельность, осуществляемая органом ГМС или МС юридического лица для проверки соблюдения установленных метрологических правил и норм. К объектам ГМКиН относятся средства измерений, эталоны, методики выполнения измерений и др. К сферам распространения ГМКиН относятся: 1) здравоохранение, экология, безопасность; 2) торговля; 3) государственные учетные операции; 4) измерения, проводимые по поручению органов суда, прокуратуры и др. органов государственного управления. Государственный метрологический контроль (ГМК) включает: 1) утверждение типа средств измерений; 2) поверку средств измерений; 3) лицензирование деятельности юридических и физических лиц по изготовлению, ремонту, продаже и прокату средств измерений. Государственный метрологический надзор (ГМН) осуществляется: 1) за выпуском, состоянием и применением СИ, аттестованными МВИ, эталонами единиц величин, соблюдением метрологических правил и норм; 2) за количеством товаров, отчуждаемых при совершении торговых операций. Этот вид надзора проводится в целях определения массы, объема, расхода или других величин, характеризующих количество товаров; 3) за количеством фасованных товаров в упаковках любого вида при их расфасовке и продаже. Он осуществляется в тех случаях, когда содержимое упаковки не может быть изменено без вскрытия или деформации, а масса, объем, длина, площадь или иные величины, указывающие количество содержащегося в упаковке товара, обозначены на упаковке.
Поверка |
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 5672; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.60.62 (0.012 с.) |

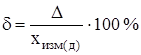 ; (5.3)
; (5.3) . (5.4)
. (5.4)












