
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные правила работы в лабораторияхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные правила работы в лабораториях Кафедры прикладной физики 1. На каждое лабораторное занятие студенты должны приносить с собой: а) лабораторный журнал (тетрадь в клетку не менее 48 листов); б) несколько листов миллиметровой бумаги формата А4; в) клей для бумаги для вклеивания графиков; г) калькулятор для инженерных расчетов (можно один на несколько человек); д) ручку, карандаш и резинку; е) линейку длиной 25 – 30 см. 2. Студенты должны быть подготовленными к выполнению каждой лабораторной работы: а) необходимо знать тему и название выполняемой работы, изучить теоретический материал по теме выполняемой работы и знать физическую сущность изучаемого явления; б) подготовить лабораторный журнал к выполнению лабораторной работы. 3. Оформление лабораторного журнала: а) на новой (правой) странице журнала должны быть написаны номер и название лабораторной работы, перечень приборов и принадлежностей, цель работы и дата проведения работы; б) далее следует изложить краткую теорию лабораторной работы, включая вывод основной рабочей формулы и формулы для оценки погрешностей результатов эксперимента. 4. Все записи в журнале выполняют аккуратно ручкой (не карандашом) на правой странице лабораторного журнала (левая предназначена для выполнения расчетов); а) отчет о лабораторной работе должен сопровождаться схемой экспериментальной установки; б) таблицы вычерчивают карандашом по линейке. Желательный размер клетки 1,5 х 2,5 см. Таблица выполняется в полном объеме для соответствующего количества измерений. В пособии к лабораторной работе изображается лишь заготовка таблицы (верхняя и нижняя ее часть). Каждую таблицу желательно вычерчивать на новой странице, оставляя место над таблицей (5см) и под таблицей (10 см). Над таблицей указывают названия приборов, класс точности и цену деления прибора.
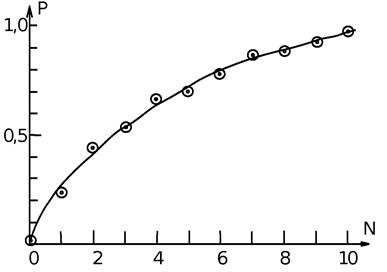
Место под таблицей необходимо для повторных измерений, если потребуется, некоторые из них можно повторить. Порядок выполнения лабораторной работы 1. Выполнение работы начинают с детального изучения лабораторной установки. Необходимо записать заводские номера измерительных приборов, их технические характеристики, цену деления шкалы приборов. Включать приборы разрешается только после проверки установки преподавателем или лаборантом; 2. Все записи необходимо делать только в лабораторном журнале и только ручкой; 3. Проведению серии измерений предшествуют пробные замеры, с помощью которых проверяют соответствие результатов измерений ожидаемым результатам, после чего приступают к основным экспериментам; 4. Данные основной серии измерений записывают в таблицу чернилами, не допуская сплошного зачеркивания, замазывания корректором или стирания результатов. Запись отсчетов производится в делениях шкалы измерительного прибора. В верхней строке таблицы указывают единицы измеряемых величин, включая множитель, на который установлен переключатель чувствительности измерительного прибора. Если был записан ошибочный результат, то его следует аккуратно зачеркнуть (так, чтобы его можно было прочитать) и записать рядом верный; 5. После выполнения измерений необходимо произвести расчеты искомых величин и их погрешностей, построить необходимые графики. Все черновые записи делаются на левой стороне листа лабораторного журнала; 6. Окончательный результат представляют в стандартном виде с указанием среднего значения измеряемой величины, абсолютной и относительной погрешностей, вычисленных по методу Стьюдента, и надежности измерений. Например, результат измерений плотности твердого тела в стандартном виде. ρ = (6,5 ± 0,3) 103 кг/м3 , ε = 5% при α = 0,95, где ρ–обозначение плотности твердого тела, 6,5 – среднее значение плотности (среднее значение величины обозначается чертой над символом, либо угловыми скобками), 0,3 – абсолютная погрешность измерения (округляется до первой значащей цифры или до первых двух, если первая значащая цифра – единица), 103 – общий множитель, ε= 5% – относительная погрешность (ε= 0,3/6,5٠100% ~ 5%), α= 0,95 – коэффициент надежности. Правила построения графиков Результаты измерений и вычислений во многих случаях удобно представлять в графическом виде. Графики строятся на миллиметровой бумаге карандашом. Размер графика - не менее половины страницы лабораторного журнала. На лист наносят координатные оси. Независимая величина (аргумент) откладывается, как правило, по горизонтали. На концах осей указывают обозначения физических величин и их размерности. Затем на оси наносят масштабные деления с удобным для прочтения интервалом. Порядок масштаба (10± п ) выносится на конец оси. Точка пересечения осей не обязательно должна соответствовать нулю по одной или обеим осям. Начало отсчета по осям и масштабы следует выбирать так, чтобы а) линия графика заняла все поле графика (рис. 1); б) наклон линии был близок к 45°. После выбора начала отсчета и масштаба по осям на лист наносятся экспериментальные точки. Их обозначают маленькими кружками, крестиками, треугольниками и т. п., размеры которых могут соответствовать погрешности измерений в масштабе графика. После этого строится собственно график, т. е. проводится плавная кривая так, чтобы она проходила как можно ближе к нанесенным точкам. График сопровождается подписью и вклеивается в лабораторный журнал. На рис.1 в качестве примера показан график зависимости степени поляризации света Р от числа стеклянных пластинок N.
Рис. 1. График зависимости степени поляризации света от числа стеклянных пластинок
Если известно из теории, что экспериментальная зависимость должна быть линейная, то по экспериментальным точкам проводится прямая, параметры которой определяются по методу наименьших квадратов (приложение I в конце сборника).
Виды измерений Измерение физической величины заключается в сравнении ее с однородной ей физической величиной, принятой за эталон. Различают прямые и косвенные измерения. При прямом измерении значение измеряемой величины определяют непосредственно с помощью измерительного прибора. При косвенном измерении значение величины находят на основе данных прямых измерений и подсчета по соответствующей формуле. Лабораторная работа № 1 Краткое описание установки
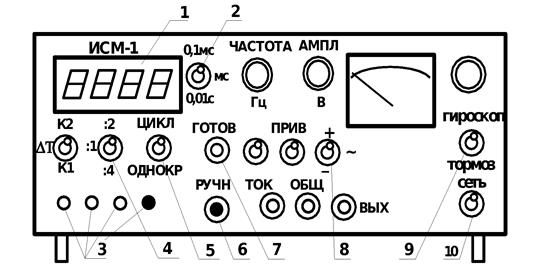
Для измерения промежутков времени в лаборатории механики используется измерительная система ИСМ–1, которая имеет достаточно широкий набор выполняемых функций: – измерение временных интервалов между различными событиями, в том числе с применением фотодатчиков; – измерение времени запаздывания и разности фаз колебаний; – управление исполнительными устройствами; – электропитание двигателя или других устройств постоянным или переменным напряжением. Органы управления системой размещены на передней панели модуля ИСМ–1 (рис.1).
Рис. 1. Передняя модель модуля ИСМ-1
В данной работе потребуются следующие органы управления: 1 – индикатор, отражающий время события в секундах или миллисекундах, в зависимости от положения переключателя 2; 3 – индикаторы включения соответствующих датчиков; 4 – переключатель количества измеряемых циклов; 5 – переключатель циклического или однократного измерения промежутка времени; 6 – кнопка ручного включения/выключения измерителя времени; 7 – кнопка приведения прибора в состояние готовности (сброс); 8 – переключатель полярности источника питания прибора (в данной работе должен стоять в верхнем или нижнем положении); 9 – включатель гироскопа; 10 – включатель прибора.
Лабораторная работа № 2 Введение
Плотность вещества характеризует распределение массы по объему тела. При равномерном распределении массы по объему (однородное тело) плотность
где т – масса тела, V – его объем, d и h – диаметр и высота цилиндра, которые измеряются с помощью штангенциркуля. В данной лабораторной работе определяется плотность ма- териала ρ, из которого изготовлены цилиндры. Расчеты завершаются определением величины доверительного интервала для плотности при заданной надежности (α = 0,95) по правилам вычисления погрешности косвенных измерений.
Порядок выполнения работы
Задание I. Измерение диаметра цилиндра
1. Измерьте 5–7 раз диаметр цилиндра d с помощью микрометра. Результаты измерений занесите в табл. 1.
2. Найдите среднее арифметическое значение диаметра по формуле
,
где п – число измерений, i – номер измерения.
3. Вычислите отклонения результатов отдельных измерений
Таблица 1 Микрометр №... Цена деления микрометра Δ= 0,01 мм, погрешность прибор δ = 0,01 мм.
4. Найдите полуширину доверительного интервала Δ d по формуле
где τ (α, n) – коэффициент Стьюдента для заданной доверительной вероятности (чаще всего выбирают α = 0,95; таблица коэффициентов Стьюдента приведена в приложении II), п–- количество измерений, δ – погрешность прибора, Δ – цена деления шкалы прибора. 5. Рассчитайте относительную погрешность ε d измерения диаметра цилиндра по формуле ε d = ( Δ d/< d >) 100%. 6. Результат измерения запишите в стандартном виде:
Задание II. Измерение высоты цилиндра
Высоту цилиндра измерьте 5–7 раз с помощью штангенциркуля, данные занесите в табл. 2. Проведите расчеты погрешности измерения высоты так же, как это было сделано в задании I.
Результат представьте в стандартном виде:
Таблица 2
Штангенциркуль № ... Цена деления штангенциркуля ω = 0,1мм, погрешность прибора δ = 0,1 мм.
Задание III. Измерение массы цилиндра
Измерьте массу цилиндра на аналитических весах с ценой деления 1 мг. В этом случае значение массы можно определить с высокой точностью, а погрешность прибора и погрешность округления массы достаточно малы, и поэтому погрешностью в определении массы цилиндра можно пренебречь. Задание IV. Вычисление плотности цилиндра и оценка погрешности косвенных измерений 1. Вычислите среднее значение плотности цилиндра по формуле
,
где < т >, <d>,<h>– средние значения массы, диаметра и высоты цилиндра. Число p= 3,14159... округлите так, чтобы его относительная погрешность была на порядок (в 10 раз) меньше наибольшей из относительных погрешностей ε d,ε h,ε m. Например, если наибольшая из этих погрешностей больше 13 %, то число следует округлить до двух значащих цифр, т.е. π ≈ 3,1. В этом случае относительная погрешность
.
Если же наибольшая относительная погрешность ε d,ε h,ε m больше 0,5%, но меньше 13%, то число следует округлить до трех значащих цифр: π = 3,14. При правильном выборе степени округления любой константы (например, числа π) погрешность округления не внесет существенного вклада в величину доверительного интервала измеряемой величины. 2. Рассчитайте относительную погрешность в определении плотности цилиндра по формуле
.
3. Рассчитайте абсолютную погрешность определения плотности цилиндра
Результат измерений запишите в стандартном виде:
Контрольные вопросы.
1. Что называется плотностью вещества? Укажите размерность плотности и единицы измерения. 2. Прямые и косвенные измерения в данной лабораторной работе. 3. Получите формулы для расчета плотности твердых тел в форме шара и параллелепипеда. Лабораторная работа № 3 Введение
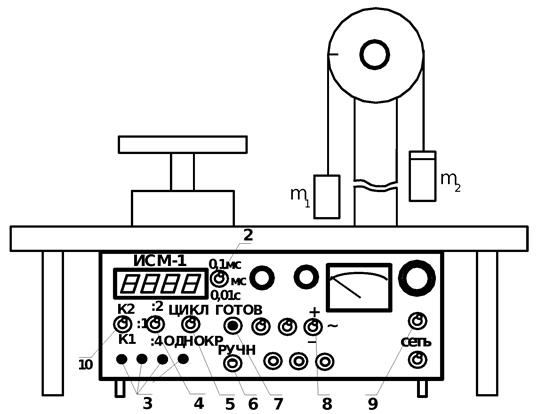
Рассмотрим движение механической системы, состоящей из вращающегося легкого блока, через который перекинута нить с привязанными грузами массами m 1и т 2(т 1 < т 2) (рис. 1).
Если нить нерастяжимая, то ускорения грузов
(3)
Разность сил натяжения (T 2 – Т 1 ) зависит от меры инертности блока (момента инерции) и трения в подшипниках блока. В предельном случае отсутствия сил трения и нулевой массы блока и нити Т 2 = Т 1 , Поэтому а ускорение свободного падения
Учтем влияние сил трения в подшипниках оси блока (пренебрегая массой блока). Введем в уравнение (3) вместо разности Т 2– Т 1«эффективную» силу сопротивления F.
При сухом трении в подшипниках и незначительном изменении массы грузов m 1и m 2 в первом приближении можно считать, что отношение
Кинематическая связь ускорения а грузов с угловым ускорением β блока при отсутствии проскальзывания нити а = β R, (7) где R – радиус блока. При равноускоренном движении угол поворота блока φ при начальной угловой скорости ωо = 0
j. (8)
Из формул (7) и (8) следует
Описание установки
Машина Атвуда представляет собой блок, закрепленный на стойке 1, через который перекинута нить. К концам нити подвешены грузы m 1и т 2(рис.2). Вращение блока регистрируется фотодатчиком, который фиксирует поворот блока на один и более оборотов.
Рмс. 2. Машина Атвуда на модуле ЛКМ-3
Задание I. Измерение ускорения свободного падения
1. Подключите датчик угла поворота блока к разъему № 2 на задней стенке модуля ИСМ – 1. Переключатель 10 переведите в положение К2. Переключатель 4 – в положение «:1», переключатель 5 - в положение «однокр», переключатель 8 - в положение «+» или «–», переключатель 9 – в среднее положение. Включите переключателем «сеть» питание модуля. Перекиньте нить через большой блок, радиус которого R = 25 мм, и закрепите на концах нити грузы примерно одинаковой массы m 1и т 2(m 1≈ т 2≈100 г, точное значение массы грузов выгравировано на каждом грузе), убедитесь, что грузы в свободном состоянии находятся в равновесии. Массу т 2 увеличьте на 10 г с помощью перегрузка. Значение массы грузов m 1и т 2с точностью до десятых долей грамма занесите в таблицу. Переведите груз m 1в нижнее положение и остановите качание второго груза. Вращая блок, добейтесь срабатывания датчика угла поворота, о чем свидетельствует загорание индикатора 3, при этом прорезь на блоке будет находиться вблизи нулевой отметки шкалы блока. Нажмите кнопку 7 «готов» и отпустите груз m 1. Система грузов придет в движение и таймер модуля ИСМ–1 зафиксирует время одного оборота блока в секундах или в миллисекундах в зависимости от положения переключателя 2. Результат измерения занесите в таблицу.
Таблица
2. Рассчитайте ускорение грузов по формуле (9). 3. Рассчитайте ускорение свободного падения g по формуле (5). 4. Повторите измерения и расчеты по пп.2–4 не менее 5 раз и рассчитайте среднее ускорение грузов а и среднее ускорение свободного падения g. 5.Замените перегрузок 10 г на другой, массой 20 г. Повторите измерения по пунктам 2-5. 6. Проведите те же опыты по п. 2 – 6 с перегрузками в 10 г и 20 г, изменив массу наборных грузов вдвое (m 1≈ т 2≈ 200 г). 7. Найдите среднее значение ускорения свободного падения g по всем измерениям. 8. Оцените абсолютную и относительную погрешность нахождения ускорения свободного падения g по методу Стьюдента. Результат запишите в стандартном виде: g = (< g > ± Δ g) (м/с2), ε =... % при а = 0,95. Задание II. Определение ускорения свободного падения с учетом трения в подшипниках оси блока Разность масс грузов в нашем эксперименте составляет всего 2 – 10 % от их суммарной массы (при большей разности масс движение грузов становится слишком быстрым, что приводит к выходу из строя установки). При этом на результаты эксперимента заметно влияет трение в подшипниках оси блока. Введя в уравнение движения грузов некоторую «эффективную» силу сопротивления F, получим уравнение движения грузов с учетом силы трения в подшипниках оси блока a (m 1 + m 2) = (m 2 – m 1) g - F, (10)
Отношение Построив график зависимости ускорения а от величины k и убедившись в том, что эта зависимость линейная, найдите g как угловой коэффициент графика. Ускорение свободного падения можно найти так же как
где Δ a – разность между ускорениями системы при разных массах, а разность Δ k = k2 – k1 вычисляется для соответствующих значений масс. Сравните результаты, полученные в первом и втором заданиях. Отношение Контрольные вопросы 1. Дайте определение кинематическим характеристикам материальной точки, движущейся прямолинейно: траектории, перемещению, пути, скорости, ускорению. 2. Дайте определение кинематическим характеристикам материальной точки, движущейся по окружности: углу поворота, угловой скорости, угловому ускорению. Какова связь между линейными и угловыми кинематическими характеристиками? 3. Что изучает динамика поступательного движения? Как вводится понятие силы, действующей на частицу, и массы частицы в динамике? Записать уравнение движения материальной частицы. 4. Как изменяется закон сухого трения в зависимости от внешнего воздействия на тело, находящегося на поверхности другого тела? От каких факторов зависит коэффициент трения? Другие виды трения. Анализ движения тела по наклонной плоскости при разных углах наклона. 5. Выведите основную рабочую формулу (5). Задания для отчета по лабораторной работе
1. Ускорение свободного падения у поверхности Луны в 6 раз меньше ускорения свободного падения у поверхности Земли. Во сколько раз выше может прыгнуть человек на Луне, чем на Земле? 2. Радиус Луны R л примерно в 3,7 раза меньше радиуса Земли R з,,,а масса Луны m л в 81 раз меньше массы Земли m з . Найти ускорение свободного падения g л у поверхности Луны. 3. На какой высоте над полюсом Земли ускорение свободного падения на убывает в 2 раза? 4. Радиус Солнца R с примерно в 110 раз больше радиуса Земли R з, а средняя плотность Солнца относится к средней плотности Земли как 1:4. Найти ускорение свободного падения у поверхности Солнца. 5. Радиус R малой планеты равен 250 км, средняя плотность 3 г/см3. Определить ускорение свободного падения g на поверхности планеты. 6. Через неподвижный блок перекинута нить, к концам которой привязаны грузы массами m 1= 2 кг и m 2 = 3 кг (см. рис.1). Найти ускорение грузов. Массой блока пренебречь, нить считать невесомой и нерастяжимой. 7. Через блок перекинута нить, на концах которой висят два груза с одинаковыми массами М. Одновременно, на каждый из грузов кладут по перегрузку: справа – массой 3 m, слева – m (рис 3.). Определить ускорение системы. 8. Через неподвижный блок перекинута нить, к которой подвешены три одинаковых груза массой m = 5 кг каждый (рис.4). Найти ускорение системы и силу натяжения нити между грузами 1 и 2.
Рис. 3 (к задаче 7) Рис. 4 (к задаче 8)
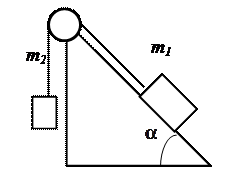
9. На углу гладкого стола укреплен неподвижный блок (рис. 5), через него перекинута нить, к концам которой привязаны грузы. Масса груза, лежащего на столе m 1 = 5 кг, масса второго груза m 2 = 2 кг. С каким ускорением движутся грузы? 10. Два груза массами m 1 и m 2 соединены легкой нерастяжимой нитью (см. рис. 5). Коэффициент трения между грузом и столом μ. Определить условие, при котором грузы будут двигаться. 11. На наклонной плоскости с углом α лежит брусок массой m 1. Груз массой m 2 присоединен к бруску при помощи нити, перекинутой через блок (рис. 6). Определить ускорение тел и силу натяжения нити.
Рис. 5 (к задаче 10) Рис. 6 (к задаче 11)
12. Три груза m, m и 4m, где m = 5 кг, соединены невесомыми нерастяжимыми нитями (рис. 7). Коэффициент трения между грузами и горизонтальной поверхностью µ = 0,3. Определить силы натяжения нитей.
Рис. 7 (к задаче 12) Рис. 8 (к задаче 13)
14. Колесо радиусом R = 10 см вращается с угловым ускорением 3,14 рад/с. Найти для точек обода к концу первой секунды угловую скорость. 15. Вал вращается с частотой 180 об/мин. С некоторого момента вал начал вращаться равнозамедленно с угловым ускорением 3 рад/с2. Через какое время вал остановится?
16. Колесо, вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса. 17. Вал вращается с частотой 180 об/мин. С некоторого момента вал начал вращаться равнозамедленно с угловым ускорением 3 рад/с2. Через какое время вал остановится? 18. Точка движется по окружности радиуса R = 20 см с постоянным тангенциальным ускорением 5 см/с2. Через какое время t после начала движения нормальное ускорение будет равно тангенциальному ускорению? 19. Колесо радиусом R = 10 см вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением 20. На наклонной плоскости с углом при основании α находится доска массой M и на ней брусок массой m (M > m) (рис. 9). Коэффициент трения между доской и плоскостью μ, между доской и бруском –2µ. Определить ускорение этих тел. При каком отношении масс тела будут находиться в равновесии?
α
Рис. 9 (к задаче 20) Лабораторная работа № 4 МАЯТНИК ОБЕРБЕКА Цель работы – изучение основного закона динамики вращательного движения, определение момента инерции системы грузов.
Приборы и принадлежности: лабораторный модуль ЛКМ-3 со стойкой и блоком, стержень с отверстиями, два круглых груза, груз наборный, нить длиной 55 см с крючком (синяя), измерительная система ИСМ-1 (секундомер), пластиковый фиксатор.
Краткая теория Основной закон динамики вращательного движения твердого тела относительно неподвижной оси
связывает кинематическую характеристику движения – угловое ускорение Угловое ускорение характеризует изменение угловой скорости во времени и направлено, как и момент силы, вдоль оси вращения. Рис. 1. Момент M силы F
Угловое ускорение связано с касательной составляющей линейного ускорения а τточки вращающегося тела соотношением
где r –- кратчайшее расстояние от этой точки до оси вращения. Моментом силы в общем случае называют векторную величину
где В уравнении (1) Момент инерции I характеризует распределение массы в твердом теле относительно оси вращения и является мерой инертности вращающегося тела. Момент инерции равен сумме произведений элементарных масс Δ mi, на которые мысленно разбито тело, на квадрат их расстояний до оси вращения I =ΣΔ mi ri . (5) Выражая Δ mi через плотность тела: Δ mi = ρ Δ Vi,где Δ Vi – элементарный объем тела, и переходя к пределу при Δ Vi → 0, получим
Формула (6) позволяет теоретически найти момент инерции любого тела. Например, момент инерции тонкого однородного стержня длиной l и массой т относительно оси, проходящей перпендикулярно стержню через его центр, I = т l 2 / 12. Теорема Штейнера устанавливает связь между моментом инерции Iс твердого тела относительно оси, проходящей через центр инерции, и моментом инерции относительно другой оси, параллельной первой I = Iс + та2 , (7) где а – расстояние между осями, т – масса тела. В настоящей работе экспериментально находится момент инерции маятника Обербека (рис.2). Он состоит из блока радиусом R, который может вращаться вокруг неподвижной горизонтальной оси. К блоку прикреплены симметрично относительнооси стержни, на каждом из которых могут свободно перемещаться грузы массами m 1, что дает возможность изменять момент инерции маятника. Грузы m 1 устанавливаются на одинаковом расстоянии от оси, так что центр инерции всей вращающейся части маятника находится на оси вращения.
.
Рис. 2. Маятник Обербека
К концу нити прикреплен груз массой m. Из закона динамики вращательного движения следует
Момент силы М, создающийся силой натяжения нити, исходя из (4)
где α – угол между вектором Запишем второй закон Ньютона для поступательного движения груза m в проекции на направление ускорения а,
В этой формуле сила натяжения нити T, действующая на груз, по модулю равна силе натяжения нити, действующей на блок в формуле (9) (поэтому они обозначены одинаково). Это справедливо, если массой нити можно пренебречь по сравнению с массой груза т. Из (9) и (10) получим
Тогда из (3) следует, (12)
Подставляя (11)и(12)в (8), получим Из этой формулы следует, что ускорение (а) не зависит от времени, так как все остальные величины в этом уравнении постоянны, значит, движение маятника будет равноускоренным и при нулевой начальной скорости.
где h – путь, пройденный грузом т за время t. В данной работе измеряется время одного полного оборота блока, и за это время груз массой m пройдет путь h =2π R. (15) Подставив (14) и (15) в (13), получим формулу для вычисления момента инерции маятника
(16)
Момент инерции маятника Обербека будет изменяться при изменении расстояния r от оси вращения маятника до центров грузов массами m 1, перемещаемых вдоль стержней. Согласно теореме Штейнера (7)
где Ic – момент инерции всей вращающейся части маятника при условии, что центры грузов m 1находились бы на оси вращения. Из (17) следует, что зависимость Описание установки
Маятник Обербека монтируется на блоке 11, закрепленном на стойке 10 модуля ЛКМ–3 (рис. 3). К блоку радиусом 25 мм прикрепляют нить, к концу которой подвешивают наборный груз массой т = 100 ÷ 200 г. На ось блока через среднее отверстие надевают стержень 12 и закрепляют его пластиковым фиксатором 13. Вращая стержень, накручивают на блок нить и поднимают груз так, чтобы он не касался стержня. При опускании груза нить приведет во вращательное движение стержень. После полного раскручивания нити стержень, продолжая вращательное движение, накрутит нить на блок и поднимет груз. При этом вращательное движение прекратится – система перейдет в начальное состояние. Время опускания и подъема груза (период колебаний маятника Обербека) зависит от многих параметров установки: длины нити, массы груза т, момента инерции стержня и блока, радиуса блока (от сил трения, толщины и массы нити, которыми мы в данной работе пренебрегаем).
Порядок выполнения работы
Задание I. Определение момента инерции стержня и блока
Подготовьте измерительную систему ИСМ–1 к работе: подключите датчик угла поворота блока к разъему 1 на задней стенке прибора, переключатель 1 поставьте в положение «К1», переключатель 4 – в положение «:1», переключатель 5 – в положение «однокр», переключатель 8 – в положение «+» или «–», переключатель 9 – в среднее положение. Включите питание модуля.
1. Закрепите конец нити на блоке так, чтобы нить не мешала креплению стержня и могла накручиваться на большой блок (R = 25 мм). Укрепите стержень на оси блока, пропустив ось блока через середину стержня, и зафиксируйте его пластиковым фиксатором. 2. Накрутите нить на блок и прикрепите наборный груз т к свободному концу нити. 3. Поверните блок
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 510; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.192.250 (0.015 с.) |

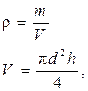
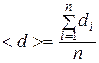
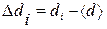 и квадрата отклонения
и квадрата отклонения 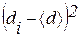 . Занесите результаты в табл. 1.
. Занесите результаты в табл. 1.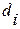

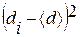

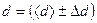 мм, ε d=... при α = 0,95.
мм, ε d=... при α = 0,95. мм, ε h =... при α= 0,95.
мм, ε h =... при α= 0,95.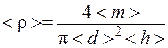
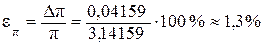
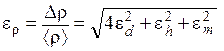
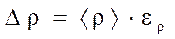 .
.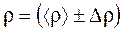 кг/м3,
кг/м3,  =... % при α = 0,95
=... % при α = 0,95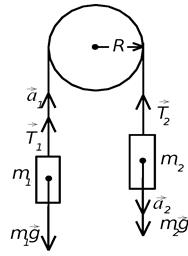 Запишем второй закон Ньютона в векторной форме для движения грузов
Запишем второй закон Ньютона в векторной форме для движения грузов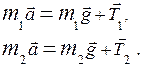 (1)
(1) . Спроецируем векторные уравнения (1) на направление ускорения движения каждого груза.
. Спроецируем векторные уравнения (1) на направление ускорения движения каждого груза.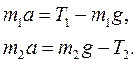 (2)
(2) Из уравнений (2) получим
Из уравнений (2) получим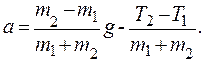
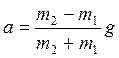 , (4)
, (4) . (5)
. (5) ,(6)
,(6) не зависит от масс грузов, а ускорение а зависит от величины k = (т 2 – m 1 )/ (m 1 + m 2 ).
не зависит от масс грузов, а ускорение а зависит от величины k = (т 2 – m 1 )/ (m 1 + m 2 ).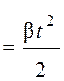
 (9)
(9)
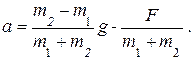 откуда
откуда (11)
(11) в случае сухого трения в первом приближении постоянно. Рассчитайте коэффициенты
в случае сухого трения в первом приближении постоянно. Рассчитайте коэффициенты 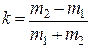 для каждого значения массы и заполните таблицу.
для каждого значения массы и заполните таблицу.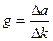 , (12)
, (12)


 13. Два груза массами m 1 = 100 г и m 2 = 50 г соединены нерастяжимой нитью, перекинутой через невесомый блок (рис. 8). Грузы прижимаются друг к другу с постоянными силами F = 1 Н. Коэффициент трения между ними µ = 0,1. Найти ускорение, с которым движутся грузы.
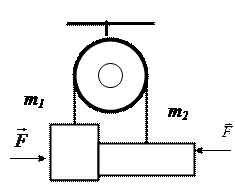
13. Два груза массами m 1 = 100 г и m 2 = 50 г соединены нерастяжимой нитью, перекинутой через невесомый блок (рис. 8). Грузы прижимаются друг к другу с постоянными силами F = 1 Н. Коэффициент трения между ними µ = 0,1. Найти ускорение, с которым движутся грузы.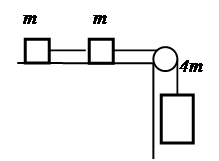
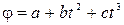 ,, где a, b, c – константы, b = 2 рад/с2, c = 1 рад/с3. Для точек, лежащих на ободе колеса, найти через время t = 2 с после начала движения: а) угловую и линейную скорости, б) угловое ускорение.
,, где a, b, c – константы, b = 2 рад/с2, c = 1 рад/с3. Для точек, лежащих на ободе колеса, найти через время t = 2 с после начала движения: а) угловую и линейную скорости, б) угловое ускорение.

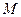

 (1)
(1)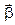 с динамическими характеристиками – моментом силы
с динамическими характеристиками – моментом силы 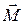 и моментом инерции I (рис. 1).
и моментом инерции I (рис. 1).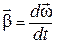 . (2)
. (2)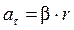 , (3)
, (3)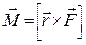 , (4)
, (4)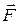 – сила, лежащая в плоскости, перпендикулярной оси вращения;
– сила, лежащая в плоскости, перпендикулярной оси вращения;  – вектор, соединяющий точку на оси c точкой приложения силы.
– вектор, соединяющий точку на оси c точкой приложения силы.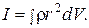 (6)
(6)
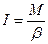 . (8)
. (8) , (9)
, (9) и отрезком R на рис. 2, равный 90°; sin α= 1.
и отрезком R на рис. 2, равный 90°; sin α= 1.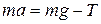 . (10)
. (10) . (11)
. (11) Тангенциальное (касательное) ускорение точек участков нити, намотанной на блок, и точек на ободе блока равны, если нет проскальзывания нити по блоку, и равны ускорению груза m, если нить нерастяжима.
Тангенциальное (касательное) ускорение точек участков нити, намотанной на блок, и точек на ободе блока равны, если нет проскальзывания нити по блоку, и равны ускорению груза m, если нить нерастяжима. (13)
(13) (14)
(14)
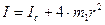 , (17)
, (17) от
от 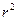 – линейная. В рассмотренной теории движения маятника Обербека не учитывались силы трения в подшипниках оси блока и сопротивление воздуха. Пренебрежение действием этих сил является главной причиной систематической погрешности измерения момента инерции.
– линейная. В рассмотренной теории движения маятника Обербека не учитывались силы трения в подшипниках оси блока и сопротивление воздуха. Пренебрежение действием этих сил является главной причиной систематической погрешности измерения момента инерции.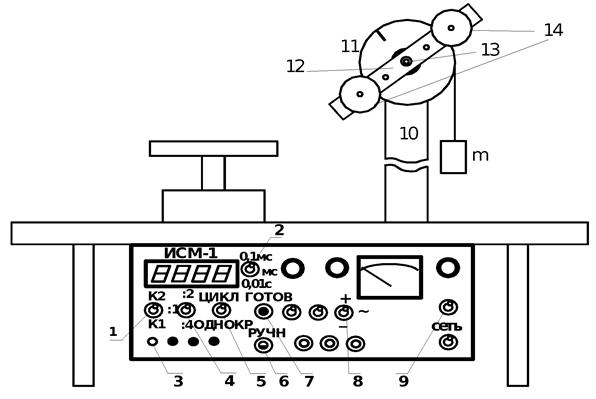 Рис. 3. Маятник Обербека на модуле ЛКМ-3
Рис. 3. Маятник Обербека на модуле ЛКМ-3


