
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование упругих колебанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы – ознакомление с характером собственных упругих колебаний, определение модуля Юнга металлов и логарифмического декремента затухания системы. Приборы и принадлежности: лабораторный модуль ЛКМ–3, набор грузов, набор упругих стержней, пружина, нить с крючком, измерительная система ИСМ-1 (секундомер). Введение
Установка для исследований упругих колебаний собрана на базе модуля ЛКМ-3 (рисунок). Упругий стержень (балка) 1 закреплен на стойке посредством цилиндрического кронштейна. К концу стержня прикреплен конец нити, перекинутой через блок. К другому концу нити прикреплен груз переменной массы, способный совершать колебания.
Рис. Установка для исследования упругих колебаний на модуле ЛКМ-3
При этом незакрепленный конец стержня колеблется в вертикальной плоскости.
(1) где m – масса груза, k – коэффициент жесткости балки. Для того чтобы не учитывать массу балки 1 и шкива при измерении жесткости балки, воспользуемся формулой
где m 1 и m 2 – масса грузов, T 1 и T 2 – соответствующие им периоды колебаний. Жесткость балки определяется ее размерами, формой, способом закрепления и модулем упругости (модулем Юнга) Е ее материала. Для круглого стержня имеем
где d – диаметр, L –- длина стержня. Порядок выполнения работы Задание I. Определение коэффициента упругости стержня 1. Соберите установку так, как это показано на рисунке. Закрепите на конце стержня 1 нить, перекиньте ее через блок и подвесьте к концу нити груз т. Стержень ориентируют перпендикулярно нити с погрешностью до 10°. 2. Измерьте линейкой 2 расстояние x 1от основания стойки до нижнего края груза.
Таблица 1
3. Измените массу груза на величину Δ m и измерьте новое расстояние х 2 . Рассчитайте коэффициент упругости стержня по формуле (4) и данные занесите в табл. 1.
4. Проделайте аналогичные измерения для других стержней. Задание II. Определение коэффициента упругости и модуля Юнга стержня методом колебаний 1. Подключите датчик угла поворота блока к разъему № 2 на задней стенке модуля ИСМ–1. Переключатель 10 переведите в положение К2. Переключатель 4 – в положение «:2», переключатель 5 – в положение «цикл», переключатель 8 - в положение «+» или «–», переключатель 9 – в среднее положение. Включите питание модуля. 2. Перекиньте нить через блок и закрепите на конце нити груз т. Поверните блок так, чтобы указатель блока совместился с нулевым делением шкалы, при этом щель диска блока должна находиться в зазоре фотодатчика так, чтобы светился индикатор 3. 3. Слегка нажав на балку, отпустите ее и измерьте период ее колебаний Т 1 с грузом m 1. Измените массу груза и измерьте период колебаний Т 2с грузом т 2. 4. Жесткость стержня рассчитайте по формуле (2), модуль Юнга по формуле (3). Данные занесите в табл. 2. Повторите измерения для других стержней.
Таблица 2
Задание III. Определение логарифмического декремента и коэффициента затухания системы с пружиной
1. Зацепите один конец пружины за крючок у основания стойки. Ко второму концу пружины прикрепите нить, перекиньте ее через блок и подвесьте к другому концу нити груз массой т. Приведите систему в колебательное движение. Измерьте период Т колебания груза. Результат запишите в табл. 3. 2. Отключите датчик угла поворота блока и переведите переключатель 4 в положение «:1». Выводя маятник из положения равновесия, отметьте его начальное отклонение х0. 3. Запустив маятник, измерьте время (с помощью кнопки 6 – «ручн»), в течение которого амплитуда колебаний уменьшится в 2 раза: x(t) = х 0/2. Измерения проведите при разных значениях отклонения х 0 и массах груза т. Результаты измерений запишите в табл. 3.
q (5)
5. Рассчитайте коэффициент затухания β по формуле (6) и заполните табл.3.
Таблица 3
Контрольные вопросы 1. Вывод уравнения гармонических колебаний для случая малых горизонтальных колебаний груза на пружине. 2. Запишите законы изменения во времени следующих параметров колебательного движения: смещения из положения равновесия, скорости и ускорения материальной частицы. 3. Как изменяется во времени энергия колеблющейся частицы? Как в этих зависимостях находит отражение закон сохранения полной механической энергии? 4. Вывод уравнения затухающих колебаний. Как соотносятся между собой периоды собственных затухающих и незатухающих колебаний? Почему затухающие колебания материальной частицы не являются гармоническими? 5. Дайте определение коэффициента затухания, логарифмического декремента затухания и добротности колебательной системы. 6. Дайте определение параметров напряженного состояния твердого тела: относительной деформации, модуля Юнга и коэффициента упругости. Сформулируйте закон Гука для твердого тела, находящегося в напряженном состоянии.
Задания для отчета по лабораторной работе
1. К вертикальной проволоке длиной L = 5 м и площадью поперечного сечения S = 2 мм2 подвешен груз массой m = 5,1 кг. В результате проволока удлинилась на x = 0,6 мм. Найти модуль упругости (модуль Юнга) материала проволоки. 2. К стальному стержню длиной L = 3 м и диаметром d = 2 см подвешен груз массой m = 2,5 103 кг. Определить напряжение σ в стержне. Модуль Юнга стали E = 220 ГПа (ГПа – ГигаПаскаль). 3. По условиям предыдущей задачи определить относительное ε и абсолютное удлинение x стержня. 4. Проволока длиной l = 2 м и диаметром d = 1 мм натянута практически горизонтально. Когда к середине проволоки подвесили груз массой m = 1 кг, проволока растянулась настолько, что точка подвеса опустилась на h = 4 см. Определить модуль Юнга E материала проволоки. 5. Тонкий стержень одним концом закреплен, к другому концу приложен момент силы M = 1 кН м. Определить угол φ закручивания стержня, если постоянная кручения C = 120 кН м /рад. 6. Коэффициент линейного теплового расширения стали равен 12 10-6 К-1, модуль Юнга E =220 ГПа (ГигаПаскаль). Какое давление p необходимо приложить к торцам стального цилиндра, чтобы длина его оставалась неизменной при повышении температуры на 100° С. 7. Стальной канат диаметром 9 мм может выдержать вес неподвижной кабины лифта. Какой диаметр должен иметь канат, если кабина лифта может иметь ускорение до 8 g. 8. Насколько вытягивается стержень из железа (модуль Юнга Е =220 ГПа), подвешенный за один конец под действием собственного веса? 9. По условиям предыдущей задачи определить, насколько меняется объем стержня. 10. Какую работу A надо совершить, чтобы растянуть на x = 1 мм стальной стержень (E = 220 ГПа) длиной l = 1 м и площадью поперечного сечения S = 1 см2. 11. Точка совершает колебания с частотой ω и коэффициентом затухания β. Найти амплитуду скорости точки как функцию времени, если в момент t = 0 амплитуда ее смещения равна a 0. 12. По условиям предыдущей задачи найти амплитуду скорости точки как функцию времени, если в момент t = 0 смещение x(0) = 0 и проекция скорости vx = v0. 13. Математический маятник совершает колебания в среде, для которой логарифмический декремент затухания θ0 = 1,5. Каким будет значение θ, если сопротивление среды увеличить в n = 2 раза?
14. По условиям предыдущей задачи определить, во сколько раз следует увеличить сопротивление среды, чтобы колебания стали невозможны? 15. К пружине подвесили груз, и она растянулась на Δ x = 9,8 см. Логарифмический декремент затухания θ = 3,1.С каким периодом будет колебаться груз в вертикальном направлении? 16. Амплитуда затухающих колебаний маятника за время t 1 = 5 мин уменьшилась в два раза. За какое время t 2, считая от начального момента, амплитуда уменьшится в восемь раз? 17. За время t = 8 мин амплитуда затухающих колебаний маятника уменьшилась в три раза. Определить коэффициент затухания β. 18. Логарифмический декремент затухания колебаний маятника равен 0,003. Определить число N полных колебаний, которые должен сделать маятник, чтобы амплитуда уменьшилась в два раза? 19. Амплитуда колебаний маятника длиной l = 1 м за время t = 10 мин уменьшилась в два раза. Определить логарифмический декремент затухания β. 20. Определить период T затухающих колебаний, если период T 0 собственных колебаний системы равен 1 с и логарифмический декремент θ = 0,628.
Приложение I Коэффициенты Стьюдента (при α= 0,95)
Приложение II
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.205.19 (0.009 с.) |


 В механике простейшими колебательными системами с одной степенью свободы являются пружинные маятники. Период колебаний Т системы, изображенной на рисунке, при малом затухании может быть рассчитан по формуле
В механике простейшими колебательными системами с одной степенью свободы являются пружинные маятники. Период колебаний Т системы, изображенной на рисунке, при малом затухании может быть рассчитан по формуле , (2)
, (2)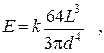 (3)
(3) . (4)
. (4) 4. Рассчитайте величину логарифмического декремента затухания по формуле
4. Рассчитайте величину логарифмического декремента затухания по формуле (6)
(6)




