
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные колебания механических системСодержание книги
Поиск на нашем сайте
СВОБОДНЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Утверждено редакционно-издательским советом университета, протокол № 1-от 20.01.05
Харьков НТУ "ХПИ" 2005 ББК 22.213 Ж 78 УДК 534.1
Рецензенты: О.К. Морачковский, д-р. техн. наук, проф. НТУ "ХПИ"; Ю.С. Воробьев, д-р. техн. наук, проф. ИПМаш НАН Украины
Ж 78 Жовдак В.А., Степченко А.С. Свободные колебания механических систем с конечным числом степеней свободы: Учеб.-метод. пособие. – Харьков: НТУ "ХПИ", 2005. – 88с. На русск. яз.
Учебно-методическое пособие содержит основы теории свободных колебаний механических систем с конечным числом степеней свободы, включая основные способы составления уравнений свободных колебаний, решение этих уравнений, определение собственных частот и форм колебаний, решение задачи о собственных колебаниях при заданных начальных условиях. Приводится расчетно-графическое задание по моделированию продольных, крутильных и изгибных колебаний роторов, в котором особое внимание уделяется построению расчетных схем исследуемых объектов. Предназначено для студентов специальностей 7.080303 "Динамика и прочность" и 7.080402 "Информационные технологии проектирования".
Навчально-методичний посібник містить основи теорії вільних коливань механічних систем з кінцевим числом степенів вільності, включаючи основні способи складання рівнянь вільних коливань, розв'язання цих рівнянь, визначення власних частот і форм коливань, розв'язання задачі про власні коливання при заданих початкових умовах. Наводиться розрахунково-графічне завдання з моделювання подовжніх, крутильних і згинальних коливань роторів, у якому особлива увага приділяється побудові розрахункових схем досліджуваних об'єктів. Призначено для студентів спеціальностей 7.080303 "Динаміка і міцність" і 7.080402 "Інформаційні технології проектування". Ил. 19. Табл. 2. Библиогр. 12 назв. ББК 22.213
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ В настоящее время без преувеличения можно отметить важнейшую роль различного рода колебательных процессов в разнообразных отраслях современной техники. Одинаковость колебательных процессов и в тоже время их отличие позволяет установить общность внутренних явлений и связей, существующих в весьма различных по своей физической природе объектах. При исследовании колебаний реальных физических объектов производится их идеализация, степень которой зависит не только от свойств рассматриваемого объекта, но и от того, каковы цели самого исследования. Конечно, если речь идет о реальной механической системе, то она обладает бесконечным числом степеней свободы. Однако при решении широкого класса задач теории колебаний достаточно ограничиться рассмотрением систем с конечным числом степеней свободы (КЧСС). В данном пособии излагаются вопросы, связанные со свободными колебаниями механических систем с КЧСС. Особое внимание уделяется построению математических моделей таких систем и различным способам составления уравнений малых свободных колебаний консервативных и диссипативных систем. Рассматриваются случаи продольных, крутильных и изгибных колебаний. Даны определения понятий собственных частот и форм колебаний, а также анализируются их основные свойства. Приводится решение задачи о свободных колебаниях при заданных начальных условиях. Представлен цикл задач о свободных продольных, крутильных и изгибных колебаниях некоторых систем, включая построение их математических моделей. Пособие рассчитано на студентов специальностей 7.080303 "Динамика и прочность" и 7.080402 "Информационные технологии проектирования", изучающих курс "Теория колебаний". Оно также будет полезно для студентов других машиностроительных специальностей. 1.Основные понятия и определения теории колебаний Понятие о колебаниях Большинство процессов, происходящих в астрономии, физике, биологии, социологии, экономике и технике, носят ярко выраженный колебательный характер. Такие процессы могут быть обусловлены различными явлениями, которые происходят в общественной жизни и экономике, нервной системе человека и животных, а также при движении планет Солнечной системы, приливах и отливах мирового океана, распространении электромагнитных и сейсмических волн и т.д. Несмотря на различную физическую сущность, внешнюю форму и назначение указанных явлений, у них наблюдается ряд общих свойств и особенностей, которые изучает теория колебаний. Поэтому несомненна большая мировоззренческая роль этой теории в понимании процессов, происходящих в целом в живой и неживой природе. В пособии будут рассмотрены только механические системы, однако основные понятия и подходы, данные в нем, вполне могут применяться и для изучения других объектов самой разнообразной физической природы. В теории колебаний главной задачей является изучение колебательных процессов. Во многих случаях установить четкую границу между колебательными и неколебательными процессами невозможно. Колебательным процессом или колебаниями называется процесс поочередного возрастания и убывания во времени какой-либо величины x(t) (рис.1.1,а) [5]. Частным случаем колебательных процессов являются периодические процессы, которые повторяются по истечении некоторого промежутка времени, называемого периодом колебаний T (рис.1.1,б). Простейший тип периодического процесса – это гармонический процесс (рис.1.1,в), который изменяется по закону синуса или косинуса:
где A – амплитуда колебаний; (wt+j) – фаза колебаний; w – угловая (круговая) частота (рад/с или с-1); j – начальная фаза (рад). Угловая частота w представляет собой число колебаний за 2p секунд. Частота колебаний может измеряться в герцах (Гц), в этом случае она обозначается через f и представляет число колебаний за секунду. Период колебаний T следующим образом связан с частотами

в Рисунок 1.1 – Виды колебательных процессов: а – произвольные колебания; б – периодические колебания; в – гармонические колебания Таким образом, гармонические колебания определяются тремя независимыми постоянными параметрами: амплитудой, частотой (периодом) и начальной фазой. Для выполнения теоретического исследования любой реальной физической системы с ее чрезвычайным многообразием свойств необходимо провести идеализацию для построения математической модели, которая описывала бы интересующие при конкретном исследовании свойства исходной системы. Характер и степень идеализаций, принимаемых при решении конкретных задач, зависят не только от свойств исходной физической системы, но и от того, на какие вопросы необходимо получить ответы при решении конкретной задачи. Поэтому при решении различных задач теории колебаний одна и та же информация может быть допустимой и недопустимой, в зависимости от того, какие характеристики исследуются. Одна идеализация свойств реальной системы позволяет получить правильное решение для определенного класса задач теории колебаний, но она может быть недопустимой при решении задач другого класса. Учитывая сложность построения математических моделей реальных объектов при решении конкретных задач теории колебаний, этот вопрос в пособии будет рассмотрен особенно внимательно.
Приведение масс Пусть элемент исходной системы состоит из n масс, которые обозначим через m 1, m 2, …, mn, а их скорости движения – через v 1, v 2, …, vn. Условием динамического приведения масс является равенство кинетических энергий приведенной массы и всех масс элемента:
откуда
где m0 – значение приведенной массы; v0 – скорость в точке приведенной массы. Таким образом, приведенная масса равна сумме произведений приводимых масс на квадраты передаточных отношений ik, где под передаточным отношением понимается
При приведении элемента конструкции с распределенной массой тоже применим принцип равенства кинетической энергии. Кинетическая энергия i -го элементарного участка длинной dx c равномерно распределенной массой равна
где Fi – площадь поперечного сечения i -го участка, Проведя суммирование по участкам и интегрирование по их длинам выражения (1.3.4), получим:
где n – число участков, Li – длина i -го участка. Условная кинетическая энергия приведенной массы m0 равна:
Окончательно получаем коэффициент приведенной массы по формуле
Данный коэффициент соответствует передаточному отношению для системы дискретных масс и позволяет получить приведенную массу для систем, где значение скорости заранее известно либо вычисляется несложно. Однако для колебательных континуальных систем, в которых преобладают изгибные, продольные или крутильные деформации, вычисление скорости в произвольной точке проблематично. В случае построения эквивалентной дискретной модели с n степенями свободы (рис. 1.3,б) для континуальной системы типа вала (рис. 1.3,а) проблемой является не только определение скоростей в точках сосредоточения масс, но и положение мест их сосредоточения. Поэтому в этих случаях используют систему статического приведения масс на основе равенства статических моментов. Это особенно эффективно, когда механическое тело – вал кусочно-постоянного поперечного сечения разбивается на участки равной длины, которые заменяются сосредоточенной в центре статической инерции массой (рис. 1.3). Преимущество статического подхода в том, что он дает ответ на два вопроса – какова величина массы и где она будет расположена.
Рисунок 1.3 – Схема приведения массы для консольной балки кусочно- постоянного поперечного сечения
Алгоритм статического подхода следующий: · континуальный вал длинной L условно разбивают на участки равной длины в соответствии с количеством дискретных масс – n, которыми он будет моделироваться (рис.1.3,а): L 1 = L 2 = ¼ = Ln -1= Ln = L / n; (1.3.8) · вычисляют массы mij для k частей вала (j = 1¸k) постоянного поперечного сечения для i -го участка длиной Li и координаты центров данной массы xцij, которые помещаются в геометрический центр части; · вычисляют массы mi для i -го участка на основе предшествующего шага (рис.1.3,б):
· записывают выражение равенства статического массового момента для i -го участка относительно неизвестной координаты центра i -й массы xцi:
· на основе выражений (1.3.9) и (1.3.10) получаем величину координаты центра i -й массы (рис.1.3,б):
При данном подходе в отличие от динамического у нас нет потери массы, что позволяет при стремлении числа масс к бесконечности получать точную модель. Однако при небольшом числе масс данный подход, очевидно, будет давать завышенные значения частот, перемещений, скоростей и других динамических характеристик. Приведение жесткостей Под жесткостью элемента механической системы понимают отношение нагрузки к вызываемой ею деформации. Для простейших деформаций вида растяжения – сжатия и кручения вала ее определяют следующим образом: · жесткость стержня, работающего на растяжение - сжатие:
· жесткость закручиваемого стержня:
где E – модуль упругости, а G – модуль сдвига; · жесткость элемента, работающего на изгиб, т.е. отношение силы к прогибу в точке приложения силы, зависит от характера заделки концов элемента, его размеров и положения силы. Поэтому в расчетной практике в этом случае удобней пользоваться величиной обратной жесткости, называемой податливостью:
Податливость устанавливает связь между деформацией q и силой Q следующего вида:
В состав упругого механизма могут быть включены элементы сложной структуры, в которой реализованы параллельные (рис. 1.4,а) или последовательные (рис. 1.4,б) соединения упругих участков.
Рисунок 1.4 – Схемы соединения жесткостей: а – параллельное соединение; б – последовательное соединение
Приведенная жесткость определяется из условия равенства потенциальной энергии приведенного упругого элемента и суммы потенциальных энергий упругих участков элемента сложной структуры. При последовательном соединении упругих участков с жесткостями С 1 и С 2 (рис. 1.4,б) равенство указанных потенциальных энергий дает
Из равенства (1.3.16) с учетом (1.3.15) и (1.3.14) получим, что при последовательном соединении складываются податливости:
Для упругого элемента, состоящего из последовательно соединенных n частей, выражение (1.3.17) имеет вид
При параллельном соединении упругих частей с жесткостями С 1 и С 2 (рис. 1.4,а), перемещения этих частей q 1, q 2 одинаковы: q 1= q 2= q (1.3.19) Поэтому из равенства потенциальных энергий с учетом (1.3.19) имеем:
А для упругого элемента состоящего из параллельно соединенных n частей выражение (1.3.20) имеет вид: С = С 1+ С 2+¼+ Сn (1.3.21)
Контрольные вопросы 1. Какие существуют основные принципы классификации колебательных процессов и колебательных систем? 2. Что общее у вынужденных колебаний и автоколебаний, свободных и параметрических колебаний, и в чем их отличие? 3. Каковы основные принципы построения дискретных моделей? 4. Привести алгоритм определения сосредоточенных масс дискретной модели. 5. Привести алгоритм определения приведенных жесткостей дискретной модели. 2.Уравнения малых колебаний систем с КЧСС относительно положения устойчивого равновесия 2.1.Основные гипотезы и определения Системы и их связи Совокупность связанных между собой материальных точек (или тел) называется механической системой. Число материальных точек, входящих в любое тело конечных размеров, необходимо считать бесконечно большим. Однако предположим, что в состав механической системы входит конечное число
Рисунок 2.1 – Система N материальных точек Пусть на положения и скорости точек системы наложены ограничения геометрического или кинематического характера, называемые связями. Эти ограничения осуществляются какими-либо другими материальными телами. Предполагается, что вне зависимости от способа реализации связей их действия на систему задаются силами, приложенными к материальным точкам и называемыми реакциями связей. Главный вектор всех реакций связей, действующих на i -ую массу обозначим · Гладкая поверхность. Препятствует поступательному перемещению тела внутрь поверхности по нормали к ней. Реакция представляет собой силу, которая направлена по общей нормали к поверхностям соприкасающихся тел в сторону от связи. · Идеальная нить. Препятствует поступательному перемещению тела вдоль нити от точки подвеса. Реакция идеальной нити представляет собой силу, которая направлена по линии нити в сторону связи. · Цилиндрический неподвижный шарнир. Препятствует поступательному перемещению тела в плоскости, перпендикулярной его оси. Реакция представляется двумя составляющими силы по осям координат в плоскости, перпендикулярной оси шарнира. · Цилиндрический подвижный шарнир. Препятствует поступательному перемещению тела перпендикулярно плоскости установки шарнира. Реакция представляется одной составляющей силы, перпендикулярной плоскости установки шарнира. · Заделка, защемление. Препятствует поступательному перемещению в любом направлении и повороту вокруг любой оси. Реакция в плоском случае представляется двумя составляющими силы и парой сил. Предполагается, что связи могут быть заданы аналитическими уравнениями, которым должны удовлетворять координаты и скорости точек системы:
В задачах механики реакции связей
Систем Система называется консервативной, если она является склерономной, на нее действуют только потенциальные силы и потенциальная энергия системы не зависит явно от времени. Полная энергия консервативной системы E, представляющая сумму кинетической T и потенциальной П, не изменяется при движении системы: E = T + П = const (2.1.8) Для таких систем зависимость (2.1.5) между обобщенными силами
Дифференциальное уравнение движения консервативной системы в обобщенных координатах может быть получено на основе уравнения Лагранжа второго рода [1,6]:
Если на систему помимо потенциальных сил, определяемых потенциалом П, действуют еще непотенциальные силы
то в этом случае [6]
Непотенциальные силы называются диссипативными, если производная от полной энергии по времени отрицательна или равна нулю:
В этом случае полная энергия системы убывает во время движения, и поэтому система называется диссипативной. Уравнение Лагранжа второго рода для такой системы имеет вид [1,6]:
Пример моделирования продольных колебаний ротора. Задание: · построить и определить параметры (массы, жесткости) для модели вала при продольных колебаниях согласно варианту задания; · получить уравнение продольных колебаний прямым способом (см. п. 2.3); · определить собственные частоты и формы колебаний (см. п. 3.2); · построить графическое изображение форм.
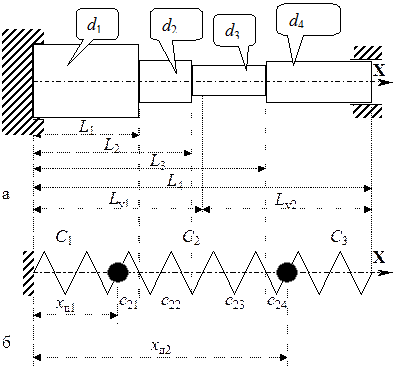
На рис. 4.1,а приведен исходный эскиз осевого сечения ротора, состоящего из четырех участков имеющих следующие размеры: L1 = 0,5 м; L2 = 0,9 м; L3 = 1,5 м; L4 = 2,0 м; d1 = 0,2 м; d2 = 0,15 м; d3 = 0,12 м; d4 = 0,15 м. Физические характеристики материала таковы: модуль упругости E = 2,1×1011 H/м2, плотность r = 8×103 кг/м3. Построение дискретной модели. Необходимо построить двухмассовую дискретную модель для моделирования колебательного процесса. Для этого ротор разбиваем на два участка равной длины: L у1 = L у2 = L 4/2.
Рисунок 4.1 – Построение модели продольных колебаний ротора: а - эскиз поперечного сечения ротора; б - дискретная модель ротора 1.Определение масс. Как видно из рис. 4.1,а, в первый участок L у1 вошло три участка ротора постоянного поперечного сечения, массы которых вычисляются по следующим формулам:
Масса первого участка определяется как сумма масс участков его составляющих: mу 1= mу 11 + mу 12 + mу 13 = 191, 261 кг. Во второй участок L у2 вошло два участка ротора постоянного поперечного сечения, массы которых вычисляются по следующим формулам:
Масса второго участка определяется как сумма масс участков его составляющих: mу 2= mу 21 + mу 22 = 115, 925 кг.
2.Вычисление центров масс. Центр каждой массы должен быть расположен в центре ее статического момента инерции. Так как исходные участки ротора имеют постоянный диаметр, их центр статического момента инерции находится в геометрическом центре участка. Найдем координаты центров масс участков постоянного поперечного сечения, составляющих первый участок:
Условия равенства массовых моментов инерции для первого участка имеют вид
откуда координата первой массы x ц 1 равна:
Аналогичным путем получим координату xц 2 второй массы:
Результаты вычислений центров масс изображены на рисунке 4.1,б.
3.Определение жесткостей. На рис. 4.1,б обозначены две полученные массы и их координаты. Эти две массы разбивают длину ротора на три участка, каждый из которых имеет жесткость, обозначенную С 1, С 2,, С 3 соответственно, и изображены как условные пружины на рис. 4.1,б. Так как первый и третий жесткостные участки соответствуют конструкционным участкам ротора постоянного диаметра, величины жесткости их равны:
Второй жесткостной участок соответствует четырем конструкционным участкам ротора, которые обозначены на рис. 4.1,б как с2i (i =1,2,3,4). Определим величины этих жесткостей:
Условные пружины с 2 i соединены последовательно, а в этом случае складываются податливости пружин, т.е. податливость пружины С 2 определяется как
откуда жесткость второй пружины равна
С 2= 2,578 109×Н/м.
Получение уравнений для свободных продольных колебаний. На рис. 4.2 изображена полученная дискретная модель ротора со степенями свободы q i (i =0, 1, 2, 3). Всего данная модель имеет четыре степени свободы, две из которых q1, q2 соответствуют массам m1, m2, а остальные безмассовым концам пружин.
Рисунок 4.2 – Дискретная модель ротора при продольных колебаниях
Применяя прямой способ, основанный на принципе Даламбера [6] (см. п. 2.3), выделим массы из системы и, заменив действие пружин упругими силами, получим уравнения равновесия в соответствии с формулой (2.3.11). Уравнение движения для двух масс и обобщенных координат, показанных на рис. 4.2, имеют вид:
Два уравнения движения содержат четыре неизвестных, поэтому для получения разрешающей системы уравнений необходимо учесть граничные условия, которые для упруго-массовой системы представленной на рис. 4.2, имеют вид:
Окончательно получаем следующую систему линейных дифференциальных уравнений относительно д вух неизвестных q1, q2:
Определение собственных частот и форм. Решение системы (4.2.1) ищем в виде (3.2.1)
где li – амплитуда колебаний; p – собственная частота колебаний; j – фазовый угол. После подстановки (4.2.2) в (4.2.1) получим уравнения форм колебаний
Из уравнений (4.2.3) получим матрицы масс и жесткости:
Частотное уравнение имеет следующий вид:
Из выражения (4.2.4) получаем биквадратное уравнение относительно собственной частоты р, которое в нормальном виде приводится ниже:
Подставив в (4.2.5) значения жесткостей и масс, получим
Решая биквадратное уравнение (4.2.6) и отбрасывая отрицательные значения, получим величины собственных частот: p1 =4289 р/с = 682,6 Гц; p2 =10010 р/с = 1594,0 Гц Как следует из уравнения форм (4.2.3), собственные формы колебаний определяются с точностью до константы. Тогда пусть для первой собственной частоты p1 выполняются равенства:
Теперь для определения первой собственной формы достаточно воспользоваться одним уравнением системы (4.2.3), подставив равенства (4.2.7):
Аналогично для второй собственной частоты p2 принимаем:
Тогда из уравнения (4.2.3) с учетом равенства (4.2.8) получаем:
В результате матрица собственных форм для ротора имеет вид
Пример моделирования крутильных колебаний ротора Задание: · построить и определить параметры (массы, жесткости) для трех- массовой модели вала при крутильных колебаниях согласно варианту задания; · получить уравнение крутильных колебаний с помощью уравнения Лагранжа (см. пп. 2.1.3, 2.2, 2.3); · определить собственные частоты и формы колебаний (см. п. 3.2); · провести нормировку форм колебаний (см. п. 3.3); · построить графическое изображение форм.
Рисунок 4.4 – Построение модели крутильных колебаний ротора а - эскиз поперечного сечения ротора; б - дискретная модель ротора
На рис. 4.4,а приведен исходный эскиз осевого сечения ротора, состоящего из четырех участков, имеющих следующие размеры: L1 = 0,5 м; L2 = 0,9 м; L3 = 1,5 м; L4 = 2,0 м; d1 = 0,2 м; d2 = 0,15 м; d3 = 0,12 м; d4 = 0,15 м. Физические характеристики материала таковы: модуль сдвига G = 8,0×1010 H/м2, плотность r = 8×103 кг/м3. Построение дискретной модели крутильных колебаний. Необходимо построить трехмассовую дискретную модель для моделирования крутильных колебаний. Для этого ротор разбиваем на три участка равной длины: L у1 = L у2 = L у3 = L 4/3. 1.Определение массовых полярных моментов инерции. Как видно из рис. 4.4,а, в первый участок L у1 вошло два участка ротора постоянного поперечного сечения, массовые полярные моменты инерции которых, вычисляют по следующим формулам:
Массовый момент первого участка определяется как сумма моментов участков его составляющих: J у1= J у11 + J у12 = 0,694 кг×м2. Во второй участок L у2 (cм. рис 4.4,а) вошли два участка ротора постоянного поперечного сечения, массы которых вычисляются по следующим формулам:
Массовый момент второго участка определяется как сумма масс участков его составляющих: J у2 = J у21 + J у22 = 0,164 кг×м2. В третий участок L у3 (cм. рис 4.4,а) вошло два участка ротора постоянного поперечного сечения, массы которых вычисляют по следующим формулам:
Массовый момент второго участка определяют как сумму масс участков его составляющих J у3= J у31 + J у32 = 0,226 кг×м2. 2.Вычисление центров массовых полярных моментов. Центр каждого эквивалентного массового полярного момента должен быть расположен так, чтобы обеспечить статическую эквивалентность модели и ротора с точки зрения массового момента инерции. Так как исходные участки ротора имеют постоянный диаметр, их центры массового полярного момента инерции находятся в геометрическом центре участка. Найдем координаты центров массовых полярных моментов инерции для частей постоянного поперечного сечения составляющих первый участок:
Условия статической эквивалентности массового полярного момента инерции для первого участка имеют вид
откуда координата центра первого массового полярного момента инерции x ц 1 равна
Аналогичным путем получим координату x ц2 для второго массового полярного момента инерции:
Аналогичным путем получим координату x ц3 для третьего массового полярного момента инерции:
Результаты вычислений центров массовых полярных моментов инерции изображены на рис. 4.4,б. 3.Определение жесткостей. На рис. 4.4,б представлена дискретная модель, состоящая из трех дисков, совершающих крутильные колебания, а также обозначены координаты их центров. Диски разбивают длину ротора на четыре участка, каждый из которых имеет жесткость обозначенную С 1, С 2,, С 3, С 4 соответственно, и изображен условной линией на рис. 4.4,б. Так как первый и четвертый жесткостные участки соответствуют конструкционным участкам ротора постоянного диаметра, величины жесткости их определяют просто:
Второй жесткостной участок соответствует трем конструкционным участкам ротора, которые обозначены на рис. 4.4,б как с 2 i (i = 1,2,3). Определим величины этих жесткостей:
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.193.141 (0.012 с.) |

 , (1.1.1)
, (1.1.1) (1.1.2)
(1.1.2)

 , (1.3.1)
, (1.3.1) , (1.3.2)
, (1.3.2) . (1.3.3)
. (1.3.3)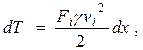 (1.3.4)
(1.3.4) g – удельная плотность материала.
g – удельная плотность материала.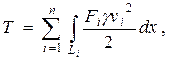 (1.3.5)
(1.3.5) (1.3.6)
(1.3.6) . (1.3.7)
. (1.3.7)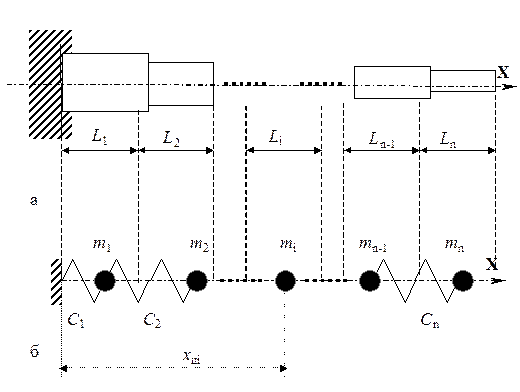
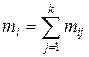 ; (1.3.9)
; (1.3.9) ; (1.3.10)
; (1.3.10) . (1.3.11)
. (1.3.11)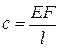 (1.3.12)
(1.3.12) , (1.3.13)
, (1.3.13) . (1.3.14)
. (1.3.14) . (1.3.15)
. (1.3.15)
 Þ
Þ  . (1.3.16)
. (1.3.16) Þ
Þ  . (1.3.17)
. (1.3.17) . (1.3.18)
. (1.3.18) Þ С = С 1+ С 2 (1.3.20)
Þ С = С 1+ С 2 (1.3.20) материальных точек, которое может быть сколь угодно большим. Рассмотрим механическую систему, состоящую из N точечных масс mi
материальных точек, которое может быть сколь угодно большим. Рассмотрим механическую систему, состоящую из N точечных масс mi  , положение которых в декартовой системе координат задается (xi yi zi) или вектором
, положение которых в декартовой системе координат задается (xi yi zi) или вектором  (Рис.2.1).
(Рис.2.1).
 (Рис.2.1). Обычно к связям можно отнести различного рода закрепления системы:
(Рис.2.1). Обычно к связям можно отнести различного рода закрепления системы:
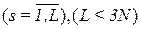 . (2.1.1)
. (2.1.1) являются неизвестными. Задаются или описываются лишь способы реализации связей. Полное определение реакций связей, т.е. определение их точек приложения, направления и величины, производится из уравнения движения системы.
являются неизвестными. Задаются или описываются лишь способы реализации связей. Полное определение реакций связей, т.е. определение их точек приложения, направления и величины, производится из уравнения движения системы.
 и потенциальной энергией
и потенциальной энергией 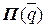 имеет вид
имеет вид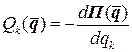



 . (2.1.13)
. (2.1.13)
 = 125,664 кг;
= 125,664 кг; = 56,549 кг;
= 56,549 кг;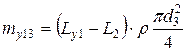 = 9,048 кг.
= 9,048 кг. = 45,239 кг;
= 45,239 кг; = 70,686 кг.
= 70,686 кг. = 0,25 м;
= 0,25 м; = 0,7 м;
= 0,7 м; = 0,95 м.
= 0,95 м. ,
,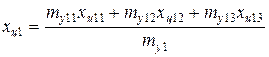 = 0,416 м.
= 0,416 м. = 1,25 м;
= 1,25 м;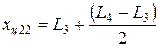 = 1,75 м;
= 1,75 м; = 1,555 м.
= 1,555 м. = 1,585×1010 Н/м.
= 1,585×1010 Н/м. = 8,339×109 Н/м.
= 8,339×109 Н/м. = 7,869×1010 Н/м;
= 7,869×1010 Н/м; = 9,278×109 Н/м;
= 9,278×109 Н/м; = 3,958×109 Н/м;
= 3,958×109 Н/м; = 6,762×1010 Н/м.
= 6,762×1010 Н/м. = 0,388×10-9 м/Н,
= 0,388×10-9 м/Н,
 ;
;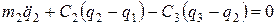 .
. ;
;  .
. (4.2.1)
(4.2.1) (4.2.2)
(4.2.2) (4.2.3)
(4.2.3)
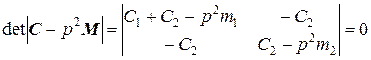 . (4.2.4)
. (4.2.4) (4.2.5)
(4.2.5) . (4.2.6)
. (4.2.6)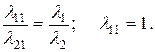 (4.2.7)
(4.2.7) .
. (4.2.8)
(4.2.8) .
. .
.
 = 0,628 кг×м2;
= 0,628 кг×м2; = 0,066 кг×м2.
= 0,066 кг×м2. = 0,093 кг×м2;
= 0,093 кг×м2; = 0,071 кг×м2.
= 0,071 кг×м2. = 0,027 кг×м2;
= 0,027 кг×м2; = 0,199 кг×м2.
= 0,199 кг×м2. = 0,25 м;
= 0,25 м; = 0,584 м.
= 0,584 м. ,
, = 0,282 м.
= 0,282 м. = 0,784 м;
= 0,784 м; = 1,117 м;
= 1,117 м;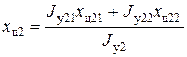 = 0,928 м.
= 0,928 м. = 1,417 м;
= 1,417 м; = 1,750 м;
= 1,750 м;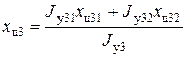 = 1,710 м.
= 1,710 м. = 4,454×107 Н×м.
= 4,454×107 Н×м. = 1,370×107 Н×м.
= 1,370×107 Н×м. = 5,761×
= 5,761× 


