
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение графического изображения собственных формСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рисунок 4.6 – Собственные формы для крутильных колебаний ротора
Пример моделирования изгибных колебаний ротора Задание: · построить и определить параметры (массы, податливости) для модели вала при изгибных колебаниях согласно варианту задания; · получить уравнение изгибных колебаний; · определить собственные частоты и формы колебаний; · построить графическое изображение форм; · определить движение по заданным начальным условиям. На рис. 4.7,а приводится исходный эскиз осевого сечения ротора, состоящего из четырех участков, имеющих следующие размеры: L1 = 0,5 м; L2 = 0,9 м; L3 = 1,5 м; L4 = 2,0 м; d1 = 0,2 м; d2 = 0,15 м; d3 = 0,12 м; d4 = 0,15 м. Физические характеристики материала таковы: модуль упругости E = 2,1×1011 H/м2, плотность r =8×103 кг/м3. Построение дискретной модели. Необходимо построить двухмассовую дискретную модель для моделирования изгибных колебаний ротора. Определение масс и центров масс Задача определения масс и центров масс для двухмассовой модели идентична задаче, решенной для продольных колебаний в п. 4.2. Поэтому приведем значения этих величин: m 1 =191, 261 кг, m 2 = 115, 925 кг; x ц1 = 0,416 м, x ц2 = 1,555 м. Построенная расчетная схема с учетом того, что граничные условия в данной модели ротора соответствуют схеме шарнирного опирания, приведена на рис. 4.7,б. Определение податливости. Для задачи изгиба ротора, более эффективно не определение жесткостей участков между массами (рис. 4.7,б), а вычисление податливости в местах расположения сосредоточенных масс. Воспользуемся интегралом Мора и правилом Верещагина [2] для определения податливости стержня кусочно-непрерывного поперечного сечения. Для этого построим две эпюры моментов от действия единичной перерезывающей силы P 1 в точке массы m 1 (рис. 4.7,в) и единичной перерезывающей силы P 2 в точке массы m 2 (рис. 4.7,д).
Рисунок 4.7 – Построение модели изгибных колебаний ротора а – эскиз поперечного сечения ротора; б – дискретная модель ротора; в – эпюра момента от силы Р1 = 1; г – эпюра момента от силы Р2 = 1
В этом случае, если разбить эпюры моментов на части, соответствующие участкам постоянного поперечного сечения и при этом эпюры моментов на участке будут иметь вид трапеции (прямоугольника или треугольника), то величины податливости в точках приложения перерезывающих сил определяются формулой
где: dij – податливость в точке i массы от действия единичной нагрузки в точке j массы; lk – длина k -го участка; Mi,k-1 – величина момента от единичной нагрузки, приложенной в точке i массы на правом конце k -го участка; Mi,k – величина момента от единичной нагрузки, приложенной в точке i массы на левом конце k -го участка; Jk – величина экваториального момента поперечного сечения k -го участка. Для определения величин моментов на эпюре от действия силы P 1 в точке массы m 1 (рис. 4.7,в), найдем реакции в опорах А и В из условий статического равновесия:
Решив систему уравнений (4.4.2), получим:
Момент в точке перегиба эпюры моментов от действия силы P 1 (максимальный момент) определяем по формуле
Теперь величины остальных моментов, показанных на рис. 4.7,в несложно получить из условия пропорциональности сторон подобных треугольников:
Моменты на опорах равны нулю, т.е. Для получения величин моментов на эпюре от действия силы P 2 в точке массы m 2 (рис. 4.7,г), аналогичным способом определим реакции в опорах А и В из условий статического равновесия:
Из решения системы уравнений (4.4.3) получим:
Момент в точке перегиба эпюры моментов от действия силы P 2 (максимальный момент) определим по формуле:
Величины остальных моментов показанных на рисунке 4.7,г получаем из условия пропорциональности сторон подобных треугольников:
Моменты на опорах равны нулю, т.е. В нашем случае эпюры моментов разбивают на шесть участков (рис. 4.7,б), так как мы имеем четыре участка равного диаметра (см. рис.4.7,а) и две сосредоточенные массы, которым соответствуют точки перегиба на эпюрах моментов (рис. 4.7,в; 4.7,г). Длины и экваториальные моменты поперечного сечения этих участков равны:
Используя выражение (4.4.1) и полученные величины моментов, длин и экваториальных моментов поперечного сечения, получаем выражения для необходимой податливости:
В силу теоремы Кастильяно о равенстве взаимных податливости имеем
Из выражения (4.4.4), с учетом (4.4.5) получим величины податливости:
Получение уравнений свободных изгибных колебаний ротора. На рис.4.8 изображена полученная дискретная модель изгибных колебаний ротора со степенями свободы y 1, y 2. Всего данная модель имеет две степени свободы, которые соответствуют сосредоточенным массам m 1, m 2.
Рисунок 4.8 –Дискретная модель ротора при изгибных колебаниях
Для получения уравнений свободных колебаний воспользуемся обратным способом составления уравнений движений (см. п. 2.3), при этом выражение (2.3.19) в обозначениях, принятых на рис. 4.8, имеет вид
Для случая модели изгибных колебаний ротора предложенной на рис. 4.8, получаем систему двух дифференциальных уравнений:
Определение собственных частот и форм. Решение системы (4.4.7) представляем в следующем виде:
где l i – амплитуда колебаний; p – собственная частота колебаний; j – фазовый угол. Подставив решение (4.4.8) в систему (4.4.7), получим систему уравнений для определения форм колебаний
Частотное уравнение в данном случае имеет вид
где матрицы податливости D и масс M получают из уравнений (4.4.9):
Из выражения (4.4.10) с учетом (4.4.11) получаем биквадратное уравнение относительно собственной частоты р:
Подставив в (4.4.12) значение величин податливости и масс, получим:
Решая уравнение (4.4.13) и отбросив отрицательные значения, получим величины собственных частот: p 1 = 422,65 р/с = 67,30 Гц; p 2 = 1367,41 р/с = 217,74 Гц. Так как собственные формы колебаний определяются с точностью до константы, пусть для первой собственной частоты выполняются равенства:
Теперь для определения первой собственной формы достаточно воспользоваться одним уравнением системы (4.4.9). Учитывая равенства (4.4.14), получаем
Аналогично для второй собственной частоты p 2 принимаем:
Тогда из уравнения (4.4.9) с учетом равенства (4.4.15) получим
В результате матрица собственных форм для изгибных колебаний ротора имеет вид
Нормировка собственных форм. Используя полученные ранее матрицу масс и вектора собственных форм, по формуле (4.3.13) получим для двух форм два нормировочных множителя: k1 =19,947, k2 =19,193. Векторы нормированных собственные форм
Построение графического изображения собственных форм. На рис. 4.9 приведено графическое изображение собственных форм для первых двух собственных частот изгибных колебаний ротора. Величины амплитуд для форм даны в нормированном виде. Как мы видим первая форма не имеет узла, а вторая имеет один узел, что соответствует теоретическим представлениям.
Рисунок 4.9 – Собственные формы изгибных колебаний ротора
Определение движения по начальным условиям. Для ротора заданы следующие начальные условия:
Решение системы (4.4.7), описывающей свободные колебания, имеет вид (4.4.8). С учетом того, что искомые амплитуды l i связаны с собственными формами соотношениями (4.4.14) и (4.4.15), а также равенства общего решения сумме частных, получаем решение в следующем виде:
Данное решение (4.4.17) можно записать в другом виде без угла сдвига по фазе aj:
Используя начальные условия (4.4.16) в решении (4.4.18) получим систему четырех уравнений с четырьмя неизвестными константами Bj и Cj (j =1,2). Так как начальные перемещения равны нулю, то константы Cj = 0 и остается система из двух уравнений:
из которой находим константы Bj:
Уравнения движения для нашей системы окончательно принимают следующий вид:
или
Варианты заданий для моделирования колебаний ротора На рис. 4.10 представлены четыре варианта конструкции ротора с разными типами подшипников – короткими и длинными, открытыми и закрытыми, которые определяют разные граничные условия. Там же указан тип дискретной модели, которую необходимо построить для моделирования продольных, крутильных или изгибных колебаниях. Порядок действий при расчете колебаний этих систем приведен в пп. 4.2, 4.3, 4.4. Варианты материалов ротора приведены в табл. 1, а в табл. 2 – варианты геометрических размеров роторов изображенных на рис. 4.10. Выбор задания производится на основе кода варианта задания, который выдает преподаватель. Например, код варианта задания "В8.Сталь–1" означает: · эскиз поперечного сечения модели ротора и типы дискретных моделей взять на рис. 4.10, вариант В; · геометрические характеристики модели приведены в табл. 2, в части "Для вариантов А,В,С", в строке № 8; · характеристики материала должны быть взяты из табл. 1 для названия "Сталь-1".
Таблица 1 – Характеристики материалов для моделей роторов
Рисунок 4.10 – Варианты моделей ротора Таблица 2 – Геометрические параметры для моделей роторов
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 433; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.70.64 (0.013 с.) |



 , (4.4.1)
, (4.4.1)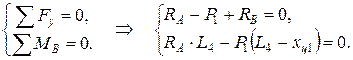 (4.4.2)
(4.4.2)




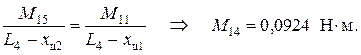

 . (4.4.3)
. (4.4.3)


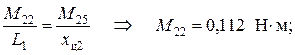








 (4.4.4)
(4.4.4)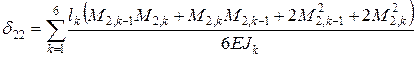
 (4.4.5)
(4.4.5)
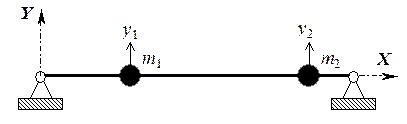
 . (4.4.6)
. (4.4.6) (4.4.7)
(4.4.7) , (4.4.8)
, (4.4.8)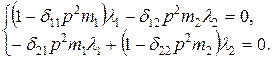 (4.4.9)
(4.4.9)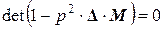 , (4.4.10)
, (4.4.10) (4.4.11)
(4.4.11) . (4.4.12)
. (4.4.12) . (4.4.13)
. (4.4.13) (4.4.14)
(4.4.14) .
. (4.4.15)
(4.4.15)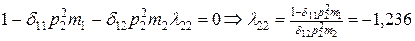 .
. .
. связаны с исходными векторами собственных форм
связаны с исходными векторами собственных форм  через выражение (4.3.14). В результате матрица нормированных собственных форм для изгибных колебаний ротора имеет вид
через выражение (4.3.14). В результате матрица нормированных собственных форм для изгибных колебаний ротора имеет вид

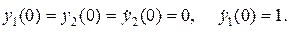 (4.4.16)
(4.4.16) (4.4.17)
(4.4.17) (4.4.18)
(4.4.18) (4.4.19)
(4.4.19) ;
; .
.


 ;
2-й подшипник –
;
2-й подшипник – 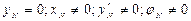 Типы дискретных моделей:
1) продольные колебания –3-массовая;
2) крутильные колебания –3-массовая;
3) изгибные колебания –2-массовая.
Типы дискретных моделей:
1) продольные колебания –3-массовая;
2) крутильные колебания –3-массовая;
3) изгибные колебания –2-массовая.

 ;
2-й подшипник –
;
2-й подшипник –  Типы дискретных моделей:
1) продольные колебания –2-массовая;
2) крутильные колебания –3-массовая;
3) изгибные колебания –2-массовая.
Типы дискретных моделей:
1) продольные колебания –2-массовая;
2) крутильные колебания –3-массовая;
3) изгибные колебания –2-массовая.


 ;
свободный край –
;
свободный край –  Типы дискретных моделей:
1) продольные колебания –3-массовая (1 от диска);
2) крутильные колебания –3-массовая;
3) изгибные колебания –2-массовая.
.
Типы дискретных моделей:
1) продольные колебания –3-массовая (1 от диска);
2) крутильные колебания –3-массовая;
3) изгибные колебания –2-массовая.
.



