
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение графического изображения собственных форм.Содержание книги
Поиск на нашем сайте
Рисунок 4.3 – Собственные формы продольных колебаний ротора Пример моделирования крутильных колебаний ротора Задание: · построить и определить параметры (массы, жесткости) для трех- массовой модели вала при крутильных колебаниях согласно варианту задания; · получить уравнение крутильных колебаний с помощью уравнения Лагранжа (см. пп. 2.1.3, 2.2, 2.3); · определить собственные частоты и формы колебаний (см. п. 3.2); · провести нормировку форм колебаний (см. п. 3.3); · построить графическое изображение форм.
Рисунок 4.4 – Построение модели крутильных колебаний ротора а - эскиз поперечного сечения ротора; б - дискретная модель ротора
На рис. 4.4,а приведен исходный эскиз осевого сечения ротора, состоящего из четырех участков, имеющих следующие размеры: L1 = 0,5 м; L2 = 0,9 м; L3 = 1,5 м; L4 = 2,0 м; d1 = 0,2 м; d2 = 0,15 м; d3 = 0,12 м; d4 = 0,15 м. Физические характеристики материала таковы: модуль сдвига G = 8,0×1010 H/м2, плотность r = 8×103 кг/м3. Построение дискретной модели крутильных колебаний. Необходимо построить трехмассовую дискретную модель для моделирования крутильных колебаний. Для этого ротор разбиваем на три участка равной длины: L у1 = L у2 = L у3 = L 4/3. 1.Определение массовых полярных моментов инерции. Как видно из рис. 4.4,а, в первый участок L у1 вошло два участка ротора постоянного поперечного сечения, массовые полярные моменты инерции которых, вычисляют по следующим формулам:
Массовый момент первого участка определяется как сумма моментов участков его составляющих: J у1= J у11 + J у12 = 0,694 кг×м2. Во второй участок L у2 (cм. рис 4.4,а) вошли два участка ротора постоянного поперечного сечения, массы которых вычисляются по следующим формулам:
Массовый момент второго участка определяется как сумма масс участков его составляющих: J у2 = J у21 + J у22 = 0,164 кг×м2. В третий участок L у3 (cм. рис 4.4,а) вошло два участка ротора постоянного поперечного сечения, массы которых вычисляют по следующим формулам:
Массовый момент второго участка определяют как сумму масс участков его составляющих J у3= J у31 + J у32 = 0,226 кг×м2. 2.Вычисление центров массовых полярных моментов. Центр каждого эквивалентного массового полярного момента должен быть расположен так, чтобы обеспечить статическую эквивалентность модели и ротора с точки зрения массового момента инерции. Так как исходные участки ротора имеют постоянный диаметр, их центры массового полярного момента инерции находятся в геометрическом центре участка.
Найдем координаты центров массовых полярных моментов инерции для частей постоянного поперечного сечения составляющих первый участок:
Условия статической эквивалентности массового полярного момента инерции для первого участка имеют вид
откуда координата центра первого массового полярного момента инерции x ц 1 равна
Аналогичным путем получим координату x ц2 для второго массового полярного момента инерции:
Аналогичным путем получим координату x ц3 для третьего массового полярного момента инерции:
Результаты вычислений центров массовых полярных моментов инерции изображены на рис. 4.4,б. 3.Определение жесткостей. На рис. 4.4,б представлена дискретная модель, состоящая из трех дисков, совершающих крутильные колебания, а также обозначены координаты их центров. Диски разбивают длину ротора на четыре участка, каждый из которых имеет жесткость обозначенную С 1, С 2,, С 3, С 4 соответственно, и изображен условной линией на рис. 4.4,б. Так как первый и четвертый жесткостные участки соответствуют конструкционным участкам ротора постоянного диаметра, величины жесткости их определяют просто:
Второй жесткостной участок соответствует трем конструкционным участкам ротора, которые обозначены на рис. 4.4,б как с 2 i (i = 1,2,3). Определим величины этих жесткостей:
Условные крутильные жесткости с 2 i соединены последовательно, а в этом случае складываются податливости пружин. Податливость пружины С 2 определяется как
откуда крутильная жесткость второго участка равна С2 = 7,396×106 Н×м. Третий жесткостной участок соответствует двум конструкционным участкам ротора, которые обозначены на рис. 4.4,б как с 3 i (i = 1,2). Определим величины этих жесткостей:
Условные крутильные жесткости с 3 i соединены последовательно, а в этом случае складываются податливости пружин:
откуда крутильная жесткость третьего участка равна С 3 = 2,469×106 Н×м. Получение уравнений для свободных крутильных колебаний. На рис. 4.5 изображена полученная дискретная модель крутильных колебаний ротора со степенями свободы fi (i = 0, 1, 2, 3, 4). Всего данная модель имеет пять степеней свободы, три из которых f 1, f 2, f 3 соответствуют массовым полярным моментам инерции J 1, J 2, J 3, а остальные две – концам упругих участков.
Рисунок 4.5 – Дискретная модель ротора при крутильных колебаниях
Для получения уравнений свободных колебаний воспользуемся уравнением Лагранжа II рода (2.1.10). Выражения для кинетической и потенциальной энергии колебательной системы, приведенной на рис. 4.5, имеют вид:
Данные уравнения необходимо дополнить граничными условиями на свободных концах ротора:
Применив уравнение Лагранжа (2..1.10) к выражениям (4.3.1) и (4.3.2) с учетом равенств (4.3.3) получаем систему дифференциальных уравнений описывающую крутильные колебания ротора:
Определение собственных частот и форм. Решение системы (4.3.4) ищем в следующем виде:
где l i - амплитуда колебаний; p - собственная частота колебаний; j - фазовый угол. После подстановки (4.3.5) в (4.3.4) получим систему уравнений для определения форм колебаний:
Частотное уравнение имеет следующий вид:
где матрицы жесткости и масс получаем из уравнения (4.3.6) в следующем виде:
Из выражения (4.3.7) получаем бикубическое уравнение относительно собственной частоты р, которое в нормальном виде приводится ниже:
Подставляя в (4.3.8) значения жесткостей и массовых полярных моментов инерции, получим
Решая уравнение (4.3.9) и отбрасывая отрицательные значения, получим следующую величину первой собственной частоты p 1 = 0; Данное решение частотного уравнения (4.3.9) соответствует движению как твердого тела (вращению вокруг оси ротора) и появляется в связи с тем, что исходный вал не был закреплен. Поэтому это решение отбрасывается, и нумерация частот будет следующая: p 1 = 3295 р/с = 524,7 Гц; p 2 = 8419 р/с = 1340 Гц. Так как собственные формы колебаний определяются с точностью до константы, пусть для первой собственной частоты выполняются равенства:
Тогда из уравнения (4.3.6) с учетом равенства (4.3.10) получаем:
Аналогично для второй собственной частоты p 2 принимаем:
Тогда из уравнения (4.3.6) с учетом равенства (4.3.11) получаем:
В результате матрица собственных форм для крутильных колебаний ротора имеет вид:
Нормировка собственных форм. Для нормировки собственных форм найдем нормировочные множители по формуле [1]
где Используя полученные ранее матрицу масс и вектора собственных форм, по формуле (4.3.13) определим для двух форм два коэффициента: k1 =1,625; k2 =2,474. Векторы нормированных собственные форм
В результате матрица нормированных собственных форм для крутильных колебаний ротора имеет вид
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.110.140 (0.008 с.) |



 = 0,628 кг×м2;
= 0,628 кг×м2; = 0,066 кг×м2.
= 0,066 кг×м2. = 0,093 кг×м2;
= 0,093 кг×м2; = 0,071 кг×м2.
= 0,071 кг×м2. = 0,027 кг×м2;
= 0,027 кг×м2; = 0,199 кг×м2.
= 0,199 кг×м2. = 0,25 м;
= 0,25 м; = 0,584 м.
= 0,584 м. ,
, = 0,282 м.
= 0,282 м. = 0,784 м;
= 0,784 м; = 1,117 м;
= 1,117 м;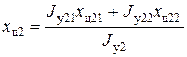 = 0,928 м.
= 0,928 м. = 1,417 м;
= 1,417 м; = 1,750 м;
= 1,750 м;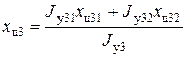 = 1,710 м.
= 1,710 м. = 4,454×107 Н×м.
= 4,454×107 Н×м. = 1,370×107 Н×м.
= 1,370×107 Н×м. = 5,761×107 Н×м.
= 5,761×107 Н×м. = 9,94×106 Н×м.
= 9,94×106 Н×м. = 5,813×107 Н×м.
= 5,813×107 Н×м. =1,352×10–7 (м×Н)-1,
=1,352×10–7 (м×Н)-1, = 0,285×107 Н×м.
= 0,285×107 Н×м. = 1,892×107 Н×м.
= 1,892×107 Н×м. = 4,050×10–7 (м×Н)–1,
= 4,050×10–7 (м×Н)–1,
 ; (4.3.1)
; (4.3.1) . (4.3.2)
. (4.3.2) (4.3.3)
(4.3.3) (4.3.4)
(4.3.4) (4.3.5)
(4.3.5) (4.3.6)
(4.3.6)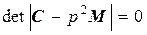 , (4.3.7)
, (4.3.7)
 (4.3.8)
(4.3.8) (4.3.9)
(4.3.9) (4.3.10)
(4.3.10)
 (4.3.11)
(4.3.11)
 .
. (4.3.13)
(4.3.13) – вектор i -й собственной формы.
– вектор i -й собственной формы. связаны с исходными векторами собственных форм
связаны с исходными векторами собственных форм  . (4.3.14)
. (4.3.14)



