
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства собственных частот и форм колебанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Исходя из данного выше определения собственных частот и форм колебаний системы с КЧСС, можно выделить следующие их основные свойства [1,3,4]: 1. Число собственных частот и форм колебаний. Система с n степенями свободы имеет n вещественных положительных собственных частот pi p1 < p2 ¼ < pn. (3.3.1) Каждой собственной частоте pi соответствует вещественная собственная форма колебаний
Число собственных форм равно числу степеней свободы n. Собственные частоты и формы колебаний системы не зависят от начальных условий, а зависят только от распределения масс и жесткостных свойств системы. 2. Ортогональность собственных форм. По определению два вектора
Рассмотрим две собственные формы колебаний
В случае симметрии матриц C и M имеют место следующие соотношения:
Подставляя соотношение (3.3.4) в левую и правую части равенства (3.3.5), получим
В полученном выражении постоянные множители ps2 и pr2 можно вынести из матричных произведений
Из соотношения (3.3.6) следует, что в формуле (3.3.8) выражения, стоящие в скобках, равны и поэтому
Так как по условию
Для доказательства условия ортогональности собственных форм относительно матрицы жесткости C воспользуемся соотношением (3.3.4), которое можно представить так:
Подставляя (3.3.11) в (3.3.10), получим
Поскольку
Условие ортогональности (3.3.10) и (3.3.13) можно представить соответственно в скалярном виде:
В полученных формулах предполагается, что 3. Узлы собственных форм. Из условий ортогональности собственных форм (3.3.14), (3.3.15) и положительности коэффициентов матриц масс и жесткости следует, что амплитуды lir и lks форм главных колебаний, соответствующие различным собственным частотам pr и ps, не могут быть все одного и того же знака. Существует закономерность в распределении числа перемен знака амплитуд собственных форм [1]. Точка, которая остается неподвижной при колебаниях по какой-либо собственной форме, называется узлом этой формы. Закономерность распределения узлов собственных форм устанавливается соответствующей теоремой об узлах собственных форм: число перемен знака (число узлов) на r -й собственной форме равно r -1 для всех
3.4 Решение задачи о свободных колебаниях Для решения задачи о свободных колебаниях механических систем с конечным числом степеней свободы необходимо решить линейное дифференциальное уравнение (2.3.1) или (2.3.2). Рассмотрим случай, когда все корни pi
Вектор амплитуды Поскольку исходная система дифференциальных уравнений (2.3.2) является линейной, то ее общее решение можно представить в виде линейной комбинации частных решений (3.4.1):
В данном выражении Сi и
или в матричной форме
Подставляя (3.4.2) в начальные условия (3.4.4), находим
Можно показать, что вектора Сi и При решении конкретных задач свободных колебаний механических систем общее решение (3.4.2) удобнее представить в виде
где Новые произвольные постоянные Ai и Bi
В скалярной форме систему линейных алгебраических уравнений (3.4.7) можно представить
Контрольные вопросы: 1. В чем отличие нормальных (главных) координат от обычных обобщенных координат? 2. В чем физический смысл приведения кинетической и потенциальной энергий к каноническому виду?
3. Дать определение собственным формам колебаний? 4. Сформулировать основные свойства собственных частот и форм колебаний? 5. Чем определяется количество собственных частот и форм колебаний механической системы? 4. Расчетно-графическое задание Колебания систем с конечным числом степеней свободы можно отнести к важнейшей и наиболее практически востребованной области теории колебаний. Наиболее наглядной частью данного направления являются продольные, крутильные и изгибные колебания стержней либо валопроводов. Построение разрешающей системы уравнений колебаний для подобных систем не представляет в настоящий момент серьезной научной проблемой. Однако далеко не очевидна задача дискретизации реальной, континуальной системы (например, валопровода [7]). Поэтому предлагаемое расчетно-графическое задание (РГЗ) предназначено для приобретения навыков дискретизации и расчета основных характеристик колебательных процессов стержневых систем.
4.1. Цели и задачи расчетно-графического задания Целью данного задания являются: · построение дискретной модели для трех видов колебаний ротора продольных, крутильных и изгибных; · запись уравнений колебаний дискретных систем в прямой и обратной форме; · построение уравнений форм колебаний и частотного уравнения; · получение решения в виде собственных частот и форм; · нормирование собственных форм по матрице масс; · графическое построение собственных форм; · получение уравнений колебаний в виде разложения по собственным формам; · графическое построение колебательного процесса. Основною задачей данного расчетно-графического задания является приобретение практических навыков дискретизации роторных и стержневых систем кусочно-непрерывной конструкции. Под кусочно-непрерывной конструкцией следует понимать роторы круглого поперечного сечения со скачкообразным изменением диаметра вала. Подобные валопроводы широко применяются в турбиностроении, двигателестроении и станкостроении. Поэтому данное РГЗ носит не только теоретический, но и практический характер. В состав РГЗ входят три задания, примеры выполнения которых, изложены ниже в пп. 4.2, 4.3 и 4.4. Варианты заданий приведены в п. 4.5. В состав РГЗ входят также две лабораторные работы на ПЭВМ по расчету методом начальных параметров продольных колебаний – «СТЕРЖЕНЬ» и изгибных колебаний «РОТОР» [10] валопроводов для тех же вариантов. Порядок действий при расчете на ПЭВМ приведен в п. 4.6.
Пример моделирования продольных колебаний ротора. Задание: · построить и определить параметры (массы, жесткости) для модели вала при продольных колебаниях согласно варианту задания; · получить уравнение продольных колебаний прямым способом (см. п. 2.3); · определить собственные частоты и формы колебаний (см. п. 3.2); · построить графическое изображение форм.
На рис. 4.1,а приведен исходный эскиз осевого сечения ротора, состоящего из четырех участков имеющих следующие размеры: L1 = 0,5 м; L2 = 0,9 м; L3 = 1,5 м; L4 = 2,0 м; d1 = 0,2 м; d2 = 0,15 м; d3 = 0,12 м; d4 = 0,15 м. Физические характеристики материала таковы: модуль упругости E = 2,1×1011 H/м2, плотность r = 8×103 кг/м3. Построение дискретной модели. Необходимо построить двухмассовую дискретную модель для моделирования колебательного процесса. Для этого ротор разбиваем на два участка равной длины:
L у1 = L у2 = L 4/2.
Рисунок 4.1 – Построение модели продольных колебаний ротора: а - эскиз поперечного сечения ротора; б - дискретная модель ротора 1.Определение масс. Как видно из рис. 4.1,а, в первый участок L у1 вошло три участка ротора постоянного поперечного сечения, массы которых вычисляются по следующим формулам:
Масса первого участка определяется как сумма масс участков его составляющих: mу 1= mу 11 + mу 12 + mу 13 = 191, 261 кг. Во второй участок L у2 вошло два участка ротора постоянного поперечного сечения, массы которых вычисляются по следующим формулам:
Масса второго участка определяется как сумма масс участков его составляющих: mу 2= mу 21 + mу 22 = 115, 925 кг.
2.Вычисление центров масс. Центр каждой массы должен быть расположен в центре ее статического момента инерции. Так как исходные участки ротора имеют постоянный диаметр, их центр статического момента инерции находится в геометрическом центре участка. Найдем координаты центров масс участков постоянного поперечного сечения, составляющих первый участок:
Условия равенства массовых моментов инерции для первого участка имеют вид
откуда координата первой массы x ц 1 равна:
Аналогичным путем получим координату xц 2 второй массы:
Результаты вычислений центров масс изображены на рисунке 4.1,б.
3.Определение жесткостей. На рис. 4.1,б обозначены две полученные массы и их координаты. Эти две массы разбивают длину ротора на три участка, каждый из которых имеет жесткость, обозначенную С 1, С 2,, С 3 соответственно, и изображены как условные пружины на рис. 4.1,б. Так как первый и третий жесткостные участки соответствуют конструкционным участкам ротора постоянного диаметра, величины жесткости их равны:
Второй жесткостной участок соответствует четырем конструкционным участкам ротора, которые обозначены на рис. 4.1,б как с2i (i =1,2,3,4). Определим величины этих жесткостей:
Условные пружины с 2 i соединены последовательно, а в этом случае складываются податливости пружин, т.е. податливость пружины С 2 определяется как
откуда жесткость второй пружины равна
С 2= 2,578 109×Н/м.
Получение уравнений для свободных продольных колебаний. На рис. 4.2 изображена полученная дискретная модель ротора со степенями свободы q i (i =0, 1, 2, 3). Всего данная модель имеет четыре степени свободы, две из которых q1, q2 соответствуют массам m1, m2, а остальные безмассовым концам пружин.
Рисунок 4.2 – Дискретная модель ротора при продольных колебаниях
Применяя прямой способ, основанный на принципе Даламбера [6] (см. п. 2.3), выделим массы из системы и, заменив действие пружин упругими силами, получим уравнения равновесия в соответствии с формулой (2.3.11). Уравнение движения для двух масс и обобщенных координат, показанных на рис. 4.2, имеют вид:
Два уравнения движения содержат четыре неизвестных, поэтому для получения разрешающей системы уравнений необходимо учесть граничные условия, которые для упруго-массовой системы представленной на рис. 4.2, имеют вид:
Окончательно получаем следующую систему линейных дифференциальных уравнений относительно д вух неизвестных q1, q2:
Определение собственных частот и форм. Решение системы (4.2.1) ищем в виде (3.2.1)
где li – амплитуда колебаний; p – собственная частота колебаний; j – фазовый угол. После подстановки (4.2.2) в (4.2.1) получим уравнения форм колебаний
Из уравнений (4.2.3) получим матрицы масс и жесткости:
Частотное уравнение имеет следующий вид:
Из выражения (4.2.4) получаем биквадратное уравнение относительно собственной частоты р, которое в нормальном виде приводится ниже:
Подставив в (4.2.5) значения жесткостей и масс, получим
Решая биквадратное уравнение (4.2.6) и отбрасывая отрицательные значения, получим величины собственных частот: p1 =4289 р/с = 682,6 Гц; p2 =10010 р/с = 1594,0 Гц Как следует из уравнения форм (4.2.3), собственные формы колебаний определяются с точностью до константы. Тогда пусть для первой собственной частоты p1 выполняются равенства:
Теперь для определения первой собственной формы достаточно воспользоваться одним уравнением системы (4.2.3), подставив равенства (4.2.7):
Аналогично для второй собственной частоты p2 принимаем:
Тогда из уравнения (4.2.3) с учетом равенства (4.2.8) получаем:
В результате матрица собственных форм для ротора имеет вид
|
||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1897; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.189.63 (0.009 с.) |

 . Предполагается, что они различны и пронумерованы в порядке возрастания
. Предполагается, что они различны и пронумерованы в порядке возрастания , которая представляет отношение амплитуд главных колебаний:
, которая представляет отношение амплитуд главных колебаний:
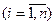 . (3.3.2)
. (3.3.2) и
и  ортогональны относительно симметричной матрицы A, если имеет место соотношение
ортогональны относительно симметричной матрицы A, если имеет место соотношение . (3.3.3)
. (3.3.3) , соответствующие s -й и r -й собственным частотам, причем
, соответствующие s -й и r -й собственным частотам, причем  . Форма колебаний
. Форма колебаний  определяется из уравнения форм колебаний (3.2.6), которое можно представить в виде
определяется из уравнения форм колебаний (3.2.6), которое можно представить в виде . (3.3.4)
. (3.3.4) ; (3.3.5)
; (3.3.5) . (3.3.6)
. (3.3.6) . (3.3.7)
. (3.3.7) . (3.3.8)
. (3.3.8) . (3.3.9)
. (3.3.9)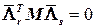 . (3.3.10)
. (3.3.10) . (3.3.11)
. (3.3.11) . (3.3.12)
. (3.3.12) , следует условие ортогональности собственных форм относительно матрицы жесткости
, следует условие ортогональности собственных форм относительно матрицы жесткости . (3.3.13)
. (3.3.13) ; (3.3.14)
; (3.3.14)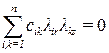 . (3.3.15)
. (3.3.15) .
. . Так например, все амплитуды li1
. Так например, все амплитуды li1  частотного уравнения (3.2.6) различны. Как было показано в разделе 3.2, каждой собственной частоте pi соответствует частное решение уравнения свободных колебаний (2.3.2), которое имеет вид:
частотного уравнения (3.2.6) различны. Как было показано в разделе 3.2, каждой собственной частоте pi соответствует частное решение уравнения свободных колебаний (2.3.2), которое имеет вид: . (3.4.1)
. (3.4.1) (3.4.2)
(3.4.2) ji произвольные постоянные, которые определяются из начальных условий
ji произвольные постоянные, которые определяются из начальных условий ,
, 
 (3.4.3)
(3.4.3) ,
,  . (3.4.4)
. (3.4.4) (3.4.5)
(3.4.5) , (3.4.6)
, (3.4.6) ;
;  .
.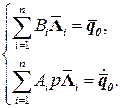 (3.4.7)
(3.4.7) (3.4.8)
(3.4.8)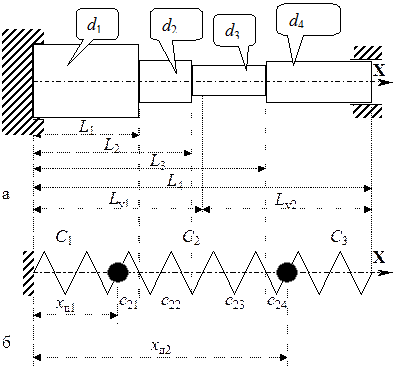
 = 125,664 кг;
= 125,664 кг; = 56,549 кг;
= 56,549 кг;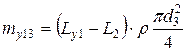 = 9,048 кг.
= 9,048 кг. = 45,239 кг;
= 45,239 кг; = 70,686 кг.
= 70,686 кг. = 0,25 м;
= 0,25 м; = 0,7 м;
= 0,7 м; = 0,95 м.
= 0,95 м. ,
,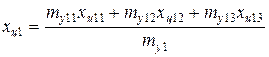 = 0,416 м.
= 0,416 м. = 1,25 м;
= 1,25 м;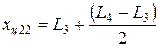 = 1,75 м;
= 1,75 м; = 1,555 м.
= 1,555 м. = 1,585×1010 Н/м.
= 1,585×1010 Н/м. = 8,339×109 Н/м.
= 8,339×109 Н/м. = 7,869×1010 Н/м;
= 7,869×1010 Н/м; = 9,278×109 Н/м;
= 9,278×109 Н/м; = 3,958×109 Н/м;
= 3,958×109 Н/м; = 6,762×1010 Н/м.
= 6,762×1010 Н/м. = 0,388×10-9 м/Н,
= 0,388×10-9 м/Н,
 ;
;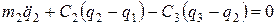 .
.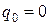 ;
;  .
. (4.2.1)
(4.2.1) (4.2.2)
(4.2.2) (4.2.3)
(4.2.3)
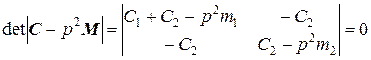 . (4.2.4)
. (4.2.4) (4.2.5)
(4.2.5) . (4.2.6)
. (4.2.6)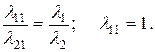 (4.2.7)
(4.2.7) .
. (4.2.8)
(4.2.8) .
. .
.


