
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обратная однократная засечкаСодержание книги
Поиск на нашем сайте
Задача определения положения точки на плоскости по трем данным точкам обратной засечкой известна под названием задачи Потенота. Об этой задаче имеется обширная литература и предложено более ста способов ее решения. Рассмотрим несколько наиболее простых и удобных способов получения координат четвертой точки по трем исходным. 1. Способ с применением формулы Деламбра. Координаты пунктов триангуляции Т1, Т2 и Т3известны (рис. 16); на определяемом пункте Р измерены углы
рис. 16
Обозначим дирекционный угол первого направления α1 и непосредственно по рис. 16, применяя формулу обратной геодезической задачи, составим уравнения
в которых три неизвестных: х, у и
Затем помножим числитель и знаменатель правой части на
Подставим правую часть выражения (78) во второе уравнение (77) и, преобразуя полученное равенство, получим
Выполняя аналогичные преобразования в третьем уравнении (77), этому уравнению придадим вид (78), а затем преобразуем к виду (79):
Из уравнения (80) вычтем уравнение (79):
Из первого уравнения (77) определим у и подставим его в полученное уравнение:
Приведя подобные члены, получим уравнение с одним неизвестным
из которого и определим его
Полученное уравнение называется формулой Деламбра. Координаты х и у можно определить, продолжив решение системы уравнений (77). Но проще определить их другим путем. Сначала определить дирекционные углы
а затем дважды определить координаты х и у из прямой засечки, вычисляемой по формулам Гаусса,
Для заключительного контроля решения задачи необходимо вторично определить дирекционный угол по формуле
Оценка точности положения пункта, определённого обратной однократной засечкой Пусть для определения координат пункта Р измерены углы
или после дифференцирования
В равенствах (87) выразим величины
(88).
Обозначим
и по аналогии с прямой однократной засечкой назовем градиентом направления.
рис. 16 С учетом обозначения (89) перепишем уравнения (88)
Для сокращения записи введем обозначения:
в соответствии с которыми уравнениям (90) можно придать вид
Решая уравнения (92) способом определителей относительно неизвестных dx и dy, получим
где
Дифференциалы dx и dy заменим случайными ошибками, от которых затем перейдем к средним квадратическим погрешностям и, учитывая, что
Так как
то
Подсчитав величины
Выражение для N с учетом (86) можно записать так:
Величины, входящие в формулы (98) и (100), можно представить графически. Для этого на направлениях РТ1, РТ2, РТ3 (см. рис. 16) отложим градиенты r1, r2, r3. Полученные точки соединим между собой и образуем треугольник
а выражение, стоящее в правой части формулы (100), — удвоенную площадь обращенного треугольника. Обозначим эту площадь через F и запишем
С учетом выражений (101) и (102), формуле (97) можно придать вид
Следовательно, точность определения положения точки, полученной обратной однократной засечкой, зависит от площади обращенного треугольника, а также от величины его двух сторон При выводе формулы (103) предполагалось, что углы Если при определяемой точке углы измеряли способом круговых приемов, то, применяя к этому случаю аналогичный вывод, можно получить
где
Сравнивая формулы (103) и (104) и полагая, что
Следовательно, измеряя углы при определяемой точке способом круговых приемов, при прочих равных условиях получим положение этой точки несколько точнее, чем при измерении отдельных углов. Рассмотрим случай, когда определяемая точка лежит на окружности проходящей через три данные точки Т1, Т2 и Т3 (рис. 17). Проведем через точку Р диаметр PQ == D и опустим из точки
Но согласно (89)
тогда
рис. 17 Следовательно, отрезок а есть величина, постоянная для всех хорд, выходящих из точки Р, а в этом случае точки Анализируя формулы (103) и (104), приходим к выводу, что задача о четвертой точке решается с наибольшей точностью в том случае, если: а) определяемая точка лежит внутри треугольника, образованного исходными пунктами; б) определяемая точка лежит вне треугольника, образован ного исходными пунктами, но против вершины между продолжениями двух сторон. Сомнительные результаты получаются тогда, когда определяемая точка находится вблизи окружности, проходящей через три исходных пункта. Задача становится неопределенной, если определяемая точка лежит на окружности. При практическом применении формул (103) и (104) поступают следующим образом. На лист бумаги наносят все исходные пункты и определяемую точку в масштабе, обеспечивающем практическое определение расстояний от искомой точки до исходных пунктов с необходимой точностью, и прочерчивают направления РТ1, РТ2 и PT3 (рис. 18).
рис. 18 По полученным с чертежа расстояниям s1, s2 и s3 по формуле (89) вычисляют величины градиентов ri, которые затем в удобном масштабе откладывают от точки Р по направлениям РТ1, PT2 и PT3. В обращенном треугольнике
после чего находят М. Величины r, а следовательно, и
где h2 и h3 — высоты обращенного треугольника, опущенные на стороны При использовании формулы (106) вычисления несколько сокращаются.
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.181.112 (0.006 с.) |

 , и
, и  а от направления Т1, принятого за начальное; требуется определить координаты пункта Р.
а от направления Т1, принятого за начальное; требуется определить координаты пункта Р.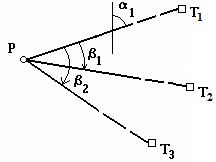
 (77),
(77),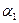 . Решив эту систему, получим дирекционный угол
. Решив эту систему, получим дирекционный угол 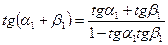 .
.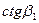
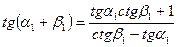 (78).
(78).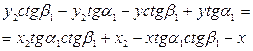 (79).
(79).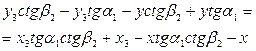 (80).
(80).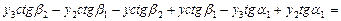
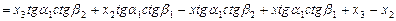
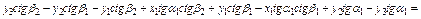
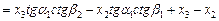 .
.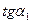
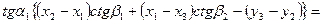

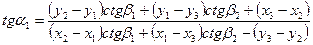 (81).
(81). и
и 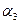 .
.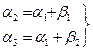 (82),
(82),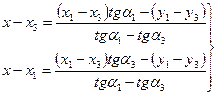 (83),
(83),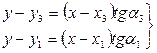 (84).
(84).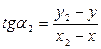 (85).
(85).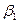 и
и 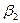 (рис. 15), которые можно представить как
(рис. 15), которые можно представить как (86),
(86), (87).
(87).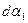 ,
, 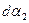 ,
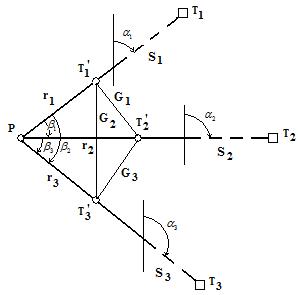
, 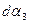 согласно дифференциальной формуле дирекционного угла через dx и dy и получим
согласно дифференциальной формуле дирекционного угла через dx и dy и получим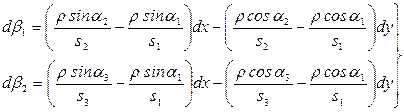
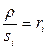 (89)
(89)
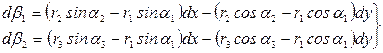 (90).
(90).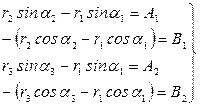 (91),
(91),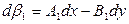
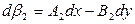 (92).
(92).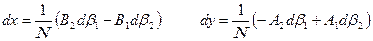 (93),
(93),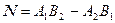 (94).
(94).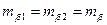 получим
получим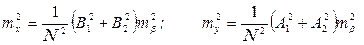 (95).
(95).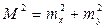 (96),
(96),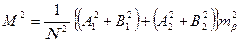 (97).
(97).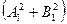 ,
, 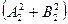 и N согласно обозначениям (91), будем иметь
и N согласно обозначениям (91), будем иметь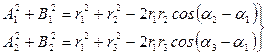 (98)
(98) (99).
(99). (100)
(100)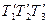 , который назовем обращенным. Обозначим стороны этого треугольника через
, который назовем обращенным. Обозначим стороны этого треугольника через 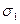 ,
, 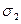 ,
, 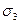 . Из рис. 16 следует, что правые части формул (98) представляют собой квадраты сторон обращенного треугольника, т. е.
. Из рис. 16 следует, что правые части формул (98) представляют собой квадраты сторон обращенного треугольника, т. е. (101),
(101),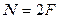 (102).
(102).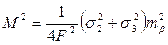 (103).
(103).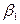 и
и  при определяемой точке измерялись каждый отдельно.
при определяемой точке измерялись каждый отдельно.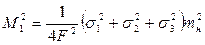 (104),
(104), — среднеквадратическая погрешность направления,
— среднеквадратическая погрешность направления, .
. , найдем
, найдем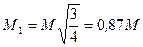 .
.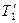 перпендикуляр ху. Тогда из двух подобных треугольников Р
перпендикуляр ху. Тогда из двух подобных треугольников Р 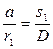 .
.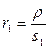 ,
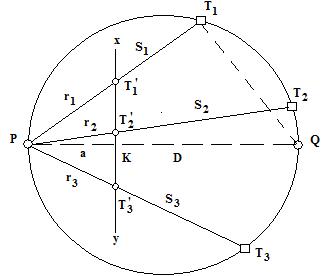
,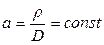 (105).
(105).
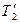 и
и 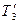 лежат на прямой ху и F = 0. Тогда формулы (103) и (104) дают:
лежат на прямой ху и F = 0. Тогда формулы (103) и (104) дают: 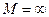 ,
, 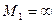 , т. е. когда искомая точка лежит на окружности, проходящей через три данные точки, определить ее положение при помощи измеренных углов
, т. е. когда искомая точка лежит на окружности, проходящей через три данные точки, определить ее положение при помощи измеренных углов 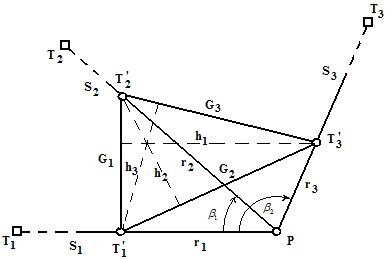
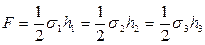 ,
,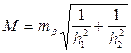 (106),
(106),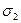 и
и 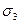 (см. рис. 18).
(см. рис. 18).


