Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обратная многократная засечкаСодержание книги
Поиск на нашем сайте
(уравнивание по измеренным направлениям) Если из измерений на определяемом пункте получены направления, то правильнее произвести уравнивание по направлениям. Как известно, измеренным направлением называется угол, отсчитанный от нулевого направления (направления нулевого радиуса лимба) до видимого направления на наблюдаемый пункт. В случае безошибочности всех наблюдений начальное и нулевое направления совпали бы, но вследствие ошибок измерений после приведения направлений к нулю нулевое направление отличается от начального на ошибку измерения последнего. Так как нулевое направление не связано с геодезическими пунктами, то в качестве неизвестных, кроме координат, приходится выбирать еще дирекционный угол нулевого направления на пункте, который называют ориентирующим углом и обозначают буквой z. Тогда
где zо—приближенное значение z; Пусть при определяемой точке имеются приведенные направления на пункты триангуляции
рис. 21 Применяя тот же ход рассуждений, что и при выводе уравнений поправок при уравнивании по углам Обратная многократная засечка (уравнивание по измеренным углам), уравнение (127) можно представить в виде
или
где Приближенное значение zo принимается равным среднему арифметическому из ориентирующих углов
Обозначим
Перепишем уравнение (128) с учетом дифференциальной формулы дирекционного угла и обозначений формул (109) и (130)
где i == 1, 2,..., n. Уравнения (131) есть параметрические уравнения поправок для случая, когда при определяемой точке измерялись направления; таких уравнении будет столько, сколько было измерено направлений, т. е. n. Поставив условие [v2] == min, придем согласно методу наименьших квадратов к трем нормальным уравнениям. Однако можно преобразовать уравнения (131), применив для этого прием, который позволит исключить неизвестное Сложим уравнения (131) и, разделив результаты на п, получим
Из уравнений (129) и (130) следует, что
поэтому уравнение (132) можно записать в виде
Вычтем члены этого равенства из соответствующих членов каждого уравнения поправок (131), тогда
где
Дальнейший ход уравнивания аналогичен ходу уравнивания результатов измерений при обратной многократной засечке по измеренным углам. При оценке точности полевых измерений вычисляется средняя квадратическая погрешность направления
где k — число неизвестных, равное трем. Пример вычислений. Обратная многократная засечка (см рис.19).
Исходные данные.
1. Определение координат пункта из обратной однократной засечки Для вычисления приближенных координат выбирают три произвольных направления и вычисляют измеренные углы βi = ni - nначальное Где βi – вычисленный измеренный угол nначальное - измеренное направление на первую выбранную точку ni - последующее выбранное направление Для решения нашей задачи взяты три первых направления. Используются формулы обратной однократной засечки:
Иcходные данные:
Многократная засечка.
I. Вычисление дирекционных углов и расстояний по приближенным координатам, вычисленным из обратной однократной засечки. Используется обратная геодезическая задача.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1206; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.223.136 (0.008 с.) |

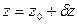 (126),
(126),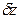 — поправка из уравнивания.
— поправка из уравнивания. ,
,  ,…,
,…,  и пусть для пункта Р из решения обратной однократной засечки найдены координаты Хo и Yo и этим значениям соответствуют приближенные дирекционные углы
и пусть для пункта Р из решения обратной однократной засечки найдены координаты Хo и Yo и этим значениям соответствуют приближенные дирекционные углы  . Согласно рис. 21, на котором через РО показано нулевое направление, будем иметь
. Согласно рис. 21, на котором через РО показано нулевое направление, будем иметь (127)
(127)
 ,
,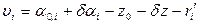 (128),
(128), — поправка к измеренному значению направления, полученная из уравнивания;
— поправка к измеренному значению направления, полученная из уравнивания;  — поправка к приближенному значению дирекционного угла.
— поправка к приближенному значению дирекционного угла. , т. е.
, т. е. (129).
(129). (130).
(130). (131),
(131),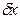 и
и  .
. (132).
(132).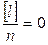
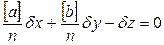 (133).
(133).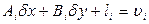 (134),
(134), (135).
(135). .
. (136),
(136),