
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Привязка к отдалённым пунктам государственной геодезической сетиСодержание книги
Поиск на нашем сайте
Координаты пункта могут быть определены прямой и комбинированной засечками с двух исходных пунктов или обратной засечкой по трем исходным пунктам. В этих случаях координаты пункта будут получены по необходимому числу исходных пунктов и измерений. Засечки, в которых используется необходимое число измерений, называют однократными. В этом случае координаты, определенные из однократных засечек, будут бесконтрольными. Для того чтобы иметь контроль правильности определения координат, найденных из засечек, необходимо использовать избыточные измерения. Засечки, в которых для получения координат пункта используют избыточное число пунктов и измерений, называют многократными.
Прямой многократной засечкой называется определение положения пункта путем измерения углов или направлений на определяемый пункт не менее чем с трех твердых пунктов, координаты которых известны. Обратной многократной засечкой называется определение положения пункта путем измерения на этом пункте углов или направлений не менее чем на четыре твердых пункта, координаты которых известны. Наличие избыточных измерений в многократных засечках приводит к уравнительным вычислениям. Метод наименьших квадратов рассматривает два основных способа уравнивания: параметрический и коррелатный. Уравнивание можно выполнять любым из этих способов. Оба дают одни и те же значения для уравниваемых величин, но объем вычислительного труда при решении конкретных задач будет разный. При уравнивании результатов измерений в многократных засечках предпочтение отдают параметрическому способу. В этом способе число нормальных уравнений, которое предстоит решать при любом числе избыточных измерений, будет равно числу неизвестных. В многократных засечках неизвестных всегда два — координаты х и у искомого пункта. Известно, что в параметрическом способе уравнивания каждое неизвестное (параметр) представляют в виде суммы двух слагаемых: приближенного значения и поправки к нему. Для искомых координат х и у пункта Р это будет выражаться так:
Приближенные значения координат xo и уо получают из решения однократных засечек, а поправки
Дифференциальные формулы дирекционного угла Пусть имеем линию АВ (рис. 9, а), координаты ее концов
Предположим, что точка В переместилась в положение В', координаты этой точки получили приращение Установим связь между изменением координат конечной точки отрезка прямой и изменением дирекционного угла этого отрезка.
рис. 9
Дифференцируя формулу для вычисления
Так как
то можно записать
Введем обозначения
тогда получим изменение дирекционного угла
Если конечная точка В линии АВ сохраняет свое положение, а перемещается начальная точка А, изменяются ее координаты на
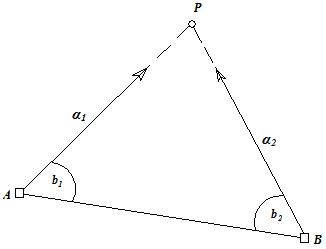
Формулы (39) и (40) называются дифференциальными формулами дирекционного угла. В общем случае (рис. 8, в), когда изменяется положение обоих концов линии АВ, дифференциальная формула принимает вид
Прямая однократная засечка Обратимся к рисунку 10. Точки А и B – имеют координаты (Xa. Ya) и (Xb. Yb). С этих точек измерены углы b1 и b2 на определяемую точку Р. Требуется определить координаты точки Р (Xр. Yр)
Рис. 10
Решение задачи сводится к определению координат точки Р – точки пересечения двух прямых АР и ВР заданных дирекционными углами α1 и α2. Для нахождения этих дирекционных углов, необходимо определить дирекционный угол направления АВ. Дирекционный угол направления АВ найдем из решения обратной геодезической задачи.
Тогда дирекционный угол направления АР (α1) для рис.10 найдем вычитанием из дирекционного угла направления АВ измеренного угла b1
Аналогично получим дирекционный угол направления ВР
Составим уравнения для данных направлений. Из решения обратной геодезической задачи следует:
Преобразуем уравнения (42)
раскроем скобки - и решим их совместно. Для этого вычтем из первого уравнения второе.
Выполнив преобразования, получим окончательный результат относительно ХР
Для определения YP можно подставить в одну из формул (42) вычисленное значение ХP и решить уравнение относительно YP. Если требуется аналитическая формула для вычисления YP, то можно взять обратную величину от формулы (42), затем решить эти уравнения совместно и получить YP.
Формулы (43) и (44) являются решением прямой однократной засечки.
Формула Юнга Рассмотрим случай, когда координаты пункта Р определяются по координатам
рис. 11 Из рис. 11 следует, что
Дирекционный угол
при этом дирекционный угол
или
Известно, что
Подставляя выражения (46) в формулы (45), получим
Из треугольника АВР следует, что
Умножив обе части этого равенства на sin А, получим
или после деления числителя и знаменателя правой части на sinAsinB —
Полученное выражение подставим в равенство (47), которое после этого несколько преобразуем, и получим окончательно
Аналогичными рассуждениями можно получить формулы вида (49) относительно пункта В. Формулами (49) часто пользуются в следующей видоизмененной записи:
Формулы вида (49, 50) носят название формул котангенсов углов треугольника, или формул Юнга. При применении формул (50) необходимо при обозначении исходных данных и измеренных углов соблюдать определенный порядок: буквой Р должен обозначаться определяемый пункт, буквой А — левый исходный пункт, буквой В — правый исходный пункт, если стоять на стороне А В лицом к пункту Р; углы треугольника будут соответственно при точках А и В, что вызывает некоторые неудобства при вычислении.
Оценка точности положения пункта, определённого прямой однократной засечкой Пусть точка Р (рис. 12) — истинное положение определяемого пункта, а точка Р1 — полученное из решения. Примем за характеристику точности определения положения
рис. 12 пункта Р среднеквадратическую погрешность Мр линейного смещения РР1. Обозначим точки пересечения направлений АР1 и ВР1 с истинными направлениями ВР и АР соответственно буквами D и Е. По малости величины РР1 по сравнению с АР и ВР фигуру РDР1Е можно принять за параллелограмм и написать
Истинные ошибки измеренных углов А и В обозначим через ΔА и ΔВ и, приняв
найдем
и
Чтобы определить среднеквадратическую погрешность Мр линейного смещения РР1, предположим, что определение пункта Р было повторено п раз и имеется п равенств вида (54). Сложив эти равенства и разделив затем обе части суммарного равенства на число п, получим
где Но
Углы А и В обычно измеряются с одинаковой точностью, т. е. тогда
или, обозначив а = s1 и b = s2,
Формулы (56) можно представить и в другом виде, если учесть, что
Тогда
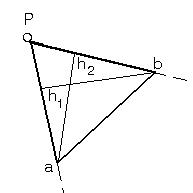
Формула (57) или (58) показывает, что среднеквадратическая погрешность положения определяемой точки будет увеличиваться главным образом с удалением ее от исходных пунктов (с увеличением s1 и s2) и уменьшением базиса засечки р. Из анализа этих формул следует, что наименьшая погрешность будет при прочих равных условиях в том случае, если угол засечки Р будет близок к 90°. Оценку точности положения пункта, определенного прямой однократной засечкой, можно также выполнить графически с помощью так называемого обращенного (или инверсионного) треугольника. Ограничимся здесь изложением практического ее применения. На листе бумаги с нанесенной координатной сеткой по координатам вершин А, В и Р строится прямая засечка в масштабе, обеспечивающем необходимую точность определения расстояний между искомой точкой и исходными пунктами (рис. 13). Затем, графически определив расстояния s1 и s2 от искомой точки до исходных пунктов, вычисляют величины Найденные градиенты откладывают на направлениях РА и РВ от точки Р и получают точки а и b, которые соединяют. Построенный треугольник аРb называется обращенным (или инвертным, инверсионным). Доказано, что формулу (56) можно преобразовать к виду
где r1, r2 — градиенты направлений; F - площадь обращенного треугольника.
рис. 13 Величина F может быть определена из выражений
где h1 и h2 — высота обращенного треугольника. С учетом этого формула (59) получит вид
Измерив на чертеже высоты h1 и h2 обращенного треугольника, которые суть перпендикуляры, опущенные из точек а и b на стороны Ра и Рb, определяют по формуле (60) среднюю квадратическую погрешность положения точки Р. Прямая многократная засечка Необходимо определить координаты пункта Р способом прямой многократной засечки, для чего с каждого исходного пункта Т1, Т2,..., Тn произведено визирование на точку Р и измерены углы
рис. 14 Как было установлено в разделе «Привязка к отдалённым пунктам государственной геодезической сети» Привязка к отдалённым пунктам государственной геодезической сети, уравнивать результаты измерений в прямой многократной засечке целесообразнее параметрическим способом.
рис. 15
Для нахождения приближенных координат Хо и Yo точки Р, используя необходимое число измерений, по формулам, указанным в разделе «Прямая однократная засечка»Прямая однократная засечка, решают прямую однократную засечку. Далее согласно параметрическому способу уравнивания следует составить уравнения поправок, в которых представить измеренные величины как функции выбранных неизвестных. Для этого рассмотрим рис. 15. Пусть приближенному значению точки Ро полученному из решения прямой однократной засечки, соответствуют координаты Хо и Yo. Точка Po близка к искомому положению точки Р, координаты которой х и у. Для линии ТiРo можно вычислить значение ее длины Si,o и дирекционного угла Уравненное значение дирекционного угла линии ТiР обозначим через
По дирекционному углу
Уравненное значение дирекционного угла будет равно измеренному значению
Запишем уравнение (63) несколько иначе:
Уравнений вида (64) будет столько, сколько измерено углов, т. е. i =1, 2,..., n. Однако в уравнении (64) пока измеренные величины не являются функцией неизвестных. Чтобы к этому перейти, проделаем следующее. Подставим в уравнение (64) значение
и обозначим
Величина li будет свободным членом уравнения поправок. Далее запишем выражение (65) с учетом (66)
Теперь в уравнении (67) от величины
Введем обозначения
Заменим в уравнении (67)
где i = 1, 2,..., n. Уравнения (69) будут параметрическими уравнениями поправок, записанными в окончательном виде. Таких уравнений будет столько, сколько наблюдаемых направлений на точку Р. Предполагая измерения углов на исходных пунктах равноточными, можно поставить при решении этих уравнений условие: [v2] = min. Cогласно методу наименьших квадратов оно приведет нас к двум нормальным уравнениям вида
Решив эти уравнения способом определителей, получим
где
Уравненные значения координат определим по формуле (36), а уравненные значения измеренных дирекционных углов — по формуле (64), значения поправок Зная координаты пункта Р (х и у), найдем
а затем Оценка точности произведенных измерений состоит в подсчете среднеквадратической погрешности угла
оценки точности уравненных значений координат — в подсчете их средних квадратических погрешностей
Веса уравненных значений координат при этом определяются из выражений
При вычислении Рх и Ру следует иметь в виду, что вес в данном случае — поименованная величина. Размерность [аа] выражается размерностью величины а в квадрате. Согласно выражениям (68) размерность
Размерность
Производить привязку полигонометрии к пунктам государственной геодезической сети способом прямой многократной засечки невыгодно с экономической точки зрения. При этом способе необходимо измерять углы на всех пунктах сети, которые, как правило, расположены на значительных расстояниях и друг от друга и от пункта, координаты которого определяют. Однако если работа проводится по хорошо продуманному плану с учетом дальнейших перспектив по сгущению обоснования, то можно значительно сократить время на переезды с одного пункта на другой, совместив измерения углов для привязочных работ с рекогносцировкой. Прямая засечка чаще находит применение при засечке боковых пунктов с пунктов полигонометрических ходов, когда измерение углов для определения координат боковых пунктов будет совмещено с измерением углов поворота при проложении полигонометрического хода.
Пример вычислений. Прямая многократная засечка. Исходные данные
Используя формулы вычисления координат из прямой однократной засечки
1. Прямая однократная засечка
2. Mногократная засечка Для вычисления свободных членов уравнений поправок необходимо вычислить приближенные дирекционные углы направлений. Для этого используются приближенные координаты из прямой однократной засечки, вычисленные в предыдущей табличке. Для вычисления приближенных дирекционных углов и расстояний используется обратная геодезическая задача.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1755; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.93.61 (0.008 с.) |

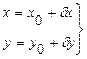 (36).
(36). и
и  — из уравнивания результатов измерений по методу наименьших квадратов параметрическим способом с использованием дифференциальных формул дирекционного угла.
— из уравнивания результатов измерений по методу наименьших квадратов параметрическим способом с использованием дифференциальных формул дирекционного угла. и
и  заданы. Дирекционный угол этой линии можно вычислить по формуле
заданы. Дирекционный угол этой линии можно вычислить по формуле .
. и
и  . В соответствии с этим дирекционный угол
. В соответствии с этим дирекционный угол  линии АВ изменится на вели чину
линии АВ изменится на вели чину 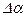 , но так как
, но так как  и
и  — величины малые, то можно считать, что угол
— величины малые, то можно считать, что угол 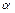 изменился на величину
изменился на величину  (
( ).
).
 .
.
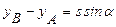 ,
, .
. (38),
(38), (39).
(39). и
и  (8, б), то очевидно, что между изменением координат точки А и изменением дирекционного угла линии АВ существует связь, выражаемая формулой (39), только коэффициенты при
(8, б), то очевидно, что между изменением координат точки А и изменением дирекционного угла линии АВ существует связь, выражаемая формулой (39), только коэффициенты при  и
и  . В этом случае формула 39 примет вид
. В этом случае формула 39 примет вид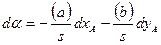 (40).
(40). (41).
(41).
 .
.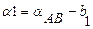 .
. .
. (42).
(42).
 ,
,
 .
.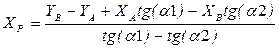 (43).
(43). (44).
(44). и
и  ,
, 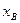 и
и  пунктов А и В, видимость между которыми имеется; углы А и В на пунктах измерены.
пунктов А и В, видимость между которыми имеется; углы А и В на пунктах измерены.

 .
. определим как разность углов
определим как разность углов ,
,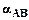 получим по координатам. Пунктов А и В из решения обратной геодезической задачи. Далее можно записать
получим по координатам. Пунктов А и В из решения обратной геодезической задачи. Далее можно записать
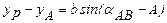 ,
, (45).
(45). (46).
(46). (47).
(47). .
.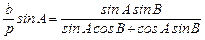 ,
,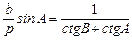 (48).
(48).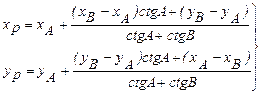 (49).
(49). (50).
(50).
 (51).
(51). ,
,  ,
, (52),
(52), (53)
(53)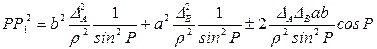 (54).
(54). ,
, ,
,  — средние квадратические погрешности измеренных значений углов А и В.
— средние квадратические погрешности измеренных значений углов А и В. при
при 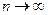 (свойство компенсации случайных погрешностей), тогда
(свойство компенсации случайных погрешностей), тогда (55).
(55). ;
;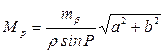 (56),
(56), (57).
(57). .
. (58).
(58). , которые называются градиентами направлений.
, которые называются градиентами направлений. (59),
(59),
 ,
, (60).
(60).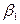 ,
,  ,...,
,...,  между линиями с известными дирекционными углами
между линиями с известными дирекционными углами  ,
,  ,…,
,…, 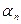 и направлениями на точку Р (рис. 14).
и направлениями на точку Р (рис. 14).

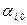 .
.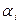 , тогда
, тогда (61).
(61).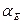 линии ТiЕ и измеренному углу
линии ТiЕ и измеренному углу 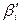 найдем «измеренное значение»
найдем «измеренное значение»  дирекционного угла линии ТiР
дирекционного угла линии ТiР (62).
(62).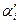 плюс поправка
плюс поправка  :
: (63).
(63). (64).
(64).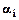 , из уравнения (61):
, из уравнения (61):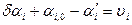 (65)
(65) (66).
(66). (67).
(67). , перейдем к величинам
, перейдем к величинам  и
и 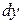 , пользуясь дифференциальной формулой дирекционного угла, согласно которой
, пользуясь дифференциальной формулой дирекционного угла, согласно которой .
. ,
, ,
, (68).
(68). , на выражение (68) и с учетом обозначений получим
, на выражение (68) и с учетом обозначений получим (69),
(69), (70).
(70). (71),
(71), (72).
(72). , для которой получим из уравнений (69).
, для которой получим из уравнений (69).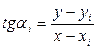 (73),
(73),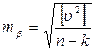 (74),
(74),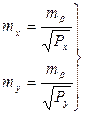 (75).
(75).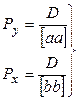 (76)
(76)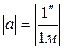 , поэтому
, поэтому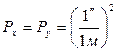 .
. так же, как и
так же, как и 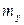 ,
, .
.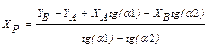 и
и  , вычислим приближенные координаты точки P. Для этого выберем из исходных данных два пункта, направления с которых на определяемый пункт Р пересекаются под углом 60° - 90° и распишем элементы формул в ниже приведенной табличке. В нашем случае подходят пункты Т1 и Т2.
, вычислим приближенные координаты точки P. Для этого выберем из исходных данных два пункта, направления с которых на определяемый пункт Р пересекаются под углом 60° - 90° и распишем элементы формул в ниже приведенной табличке. В нашем случае подходят пункты Т1 и Т2.


