Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение длины и дирекционного угла истинной замыкающей хода.Содержание книги
Поиск на нашем сайте
а) Найдем приращения истинных координат и длину замыкающей линии хода R1 между пунктами ГГС Т1 и Т2. D xист = XТ2 - XТ1 D yист = YТ2 - YТ1 ; б). Определим румб истинной замыкающей R1.
По известным правилам, от румба линии перейдем к дирекционному углу a.
Определение приращений координат, длины и дирекционного угла замыкающей хода с произвольно заданным дирекционным углом первой измеренной линии. а) Зададим первой линии хода произвольный дирекционный угол a‘ и определим по известным зависимостям последующие дирекционные углы линий хода. ai+1‘= ai‘+bi изм ± 180°. Как правило, дирекционному углу первой линии задают значение a‘ = 0. б). По измеренным линиям и вычисленным дирекционным углам найдем приращения координат поворотных точек хода Dx’i = Si cos(ai‘); Dy’i= Si sin(ai‘); в). Просуммируем приращения координат и определим длину замыкающей проложенного хода R1’. Оценим качество измерений. По определению, длина радиус-вектора не зависит от угла его поворота. Тогда можно записать R = R’ Однако ввиду неизбежных ошибок измерений данное соотношение выполняться не будет, а будет верно равенство R - R1’= dr, где dr - линейная невязка хода fs , которая является совокупностью ошибок линейных и угловых измерений. Если выполняется соотношение dr/R £ 1/ T; где 1/Т - заданная относительная погрешность то вычисления можно продолжить, в противном случае, присутствуют грубые ошибки измерений, которые необходимо исключить, выполнив повторные измерения. г). Определение угла доворота d a вычисленной замыкающей линии хода - R’ По вычисленной сумме приращений координат измеренных линий найдем румб r’ - вычисленной замыкающей.
от которого перейдем к дирекционному углу a ‘. Чтобы получить истинные приращения координат необходимо развернуть R’ с заданным углом a ‘ в направлении R с заданным истинным углом a. Для этого определим угол доворота da линии R’. da = a - a ‘. Введя поправку da в начальный, произвольно взятый дирекционный угол a ‘ a ‘испр = a ‘ + da и исправив последующие дирекционные углы за da, окончательно определим исправленные приращения координат. (Если a ‘- дирекционный угол первой линии =0, то da =a ‘испр – искомый дирекционный угол первой стороны вычисляемого хода)
На этом первое приближение заканчивается. Второе приближение Далее используется стандартный алгоритм вычисления рабочих координат. Отличие состоит в том, что в данном алгоритме отсутствует угловая невязка, которая скомпенсировалась доворотом хода – замыкающая хода совпадает с истинной замыкающей. Пример вычисления рабочих координат полигонометрического хода (координатная привязка). Рассмотрен предыдущий пример.Исходные дирекционные углы изъяты из вычислений Первое приближение
После того, как в первом приближении вычислили угол доворота и дирекционный угол замыкающей, выполняют второе приближение, в котором вычисляют окончательные координаты точек хода. Для этого первая измеренная линия хода принимает значение вычисленного дирекционного угла. Второе приближение
Косвенная привязка к пунктам ГГС
а) привязка к близлежащим пунктам; б) привязка к отдаленным пунктам. Используя различные способы привязки, можно получить также координаты ряда боковых пунктов. Рассмотрим указанные способы привязки.
Передача координат с вершины знака на землю (снесение координат) Этот вид привязки полигонометрического хода применяется тогда, когда пункт государственной геодезической сети недоступен для непосредственных измерений, но имеется возможность подойти к нему на расстояние порядка 100—500 м. На практике могут иметь место следующие случаи: 1) пункт недоступен ни для линейных, ни для угловых измерений; 2) пункт доступен для угловых измерений, но недоступен для линейных измерений. Рассмотрит оба случая.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1027; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.36.146 (0.011 с.) |

 .
. .
.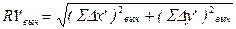 .
. ,
,