
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Журнал измерения углов способом круговых приемов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пункт 9. Прием I. Ноября 2007 года. Погода: ясно, ветер слабый Видимость: хорошая Наблюдатель: Cтепанов П.Г. Вычислитель: Сержантова Р.А.
Если Δср > 0, то требуется рапределение невязки за “не замыкание горизонта” с обратным знаком на все направления, пропорционально их номерам. Поправки в средние направления вычисляют по формуле:
где n’ – число направлений; i - порядковый номер направления. Значения приведенных к общему нулю направлений получают, вычитая среднее значение первого направления из каждого последующего, исправленного за поправку σi Колебания направлений в отдельных приемах не должно превышать ±8". В случае несоблюдения данного допуска прием вычеркивается и переделывается. Прием переделывается при той же установке начального направления. Вся программа измерения углов переделывается полностью в том случае, если количество переделываемых приемов ≥ 30%. Окончательное значение направлений получают как среднее арифметическое из направлений, измеренных в отдельных приемах.
Оценка точности угловых измерений. а) В одиночном полигонометрическом ходе оценка точности состоит в получении СКП собственно измерения угла m’b, которую вычисляют а) по уклонениям vb отдельных приемов от среднего
где n’ -число приемов измерений; k -число пунктов хода, на которых производились измерения.
б) По разности db между приемами
При вычислении значений m'β по приведенным формулам не учитываются погрешности центрирования, редукции и погрешности связанные с внешними условиями. Поэтому погрешность m'β , вычисленная по приведенным формулам, будет примерно в два раза меньше полной средней квадратической погрешности угла mβ . Средняя квадратическая погрешность самой погрешности измеренного угла mβ, вычисленная по формуле 5 и 6 определяется по формуле
Пример В полигонометрическом ходу 4 класса измерено 5 углов 6 приемами каждый. Для измерения углов использовался теодолит 3Т2КП. Вычислить среднюю квадратическую погрешность собственно измерения угла по уклонениям каждого приема от их средних значений. Таблица 8
б) В системе ходов Предварительную оценку точности угловых измерений можно выполнить по приведенным выше формулам. Окончательную оценку точности выполняют по угловым невязкам ходов или полигонов, а так же по поперечным невязкам вытянутых ходов. a) Если известны угловые невязки fβ по N ходам или полигонам, то среднюю квадратическую погрешность угла определяют по формуле 8
где n - число углов в каждом ходе или полигоне. Среднюю квадратическую погрешность самой погрешности измерения углов находят по формуле 9
Пример Вычислить среднюю квадратическую погрешность измерения угла по угловым невязкам 8 ходов (таблица 9). Таблица 9
б) Если известны поперечные невязки по N вытянутым ходам, то среднюю квадратическую погрешность угла определяют по формуле 10 и 11
или
где u - поперечные невязки вытянутых ходов, вычисленные по углам, исправленным за угловую невязку; u' - поперечные невязки вытянутых ходов, вычисленные по неисправленным за угловую невязку углам;
Поперечная невязка u вычисляется по формуле:
где L -длина замыкающей хода
u' связанас u следующим соотношением:
В случае, если влияние погрешностей исходных данных на величины невязок ничтожны по сравнению с влиянием погрешностей полевых измерений, то формулы 8,10, 11 дадут близкие между собой значения mβ, которые действительно характеризуютточность угловых измерений. В случае, если влияние погрешностей исходных данных будет заметным, результаты вычислений по формулам 8, 10 и 11 дадут преувеличенные и не согласующиеся между собой результаты. Причем наибольшее отличие от истинных результатов даст формула 10, как наиболее чувствительная к погрешностям исходных данных, а наименьшее – формула 8, значение которой принимают за наиболее близкую к истинной величине.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 844; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

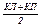

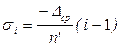 (4);
(4); (5);
(5); (6).
(6). (7).
(7). ;
;  .
. (8);
(8);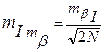 (9).
(9).
 ;
;  .
. (10),
(10), (11),
(11),

 ( 12 )
( 12 )




