
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление координат пунктов разомкнутого линейно-углового ходаСодержание книги
Поиск на нашем сайте Каждый определяемый пункт линейно-углового хода имеет две координаты X и Y, которые являются неизвестными и которые нужно найти. Общее количество пунктов в ходе обозначим через n, тогда количество неизвестных будет 2 * (n - 2), так как у двух пунктов (исходных начального и конечного) координаты известны. Для нахождения 2 * (n - 2) неизвестных достаточно выполнить 2 * (n - 2) измерений. Подсчитаем, сколько измерений выполняется в разомкнутом линейно-угловом ходе: на n пунктах измерено n углов - по одному на каждом пункте, измерены также (n - 1) сторон хода, всего получается (2 * n - 1) измерений (рис.2.18). Разность между количеством выполненных измерений и количеством необходимых измерений равна:
то-есть, три измерения являются избыточными: это угол на предпоследнем пункте хода, угол на последнем пункте хода и последняя сторона хода. Но тем не менее, эти измерения выполнены, и их необходимо использовать при вычислении координат пунктов хода. В геодезических построениях каждое избыточное измерение порождает какое-либо условие, поэтому количество условий равно количеству избыточных измерений; в разомкнутом линейно-угловом ходе должны выполняться три условия: условие дирекционных углов и два координатных условия. Условие дирекционных углов. Вычислим последовательно дирекционные углы всех сторон хода, используя формулу передачи дирекционного угла на последующую сторону хода:
Сложим эти равенства и получим:
Это - математическая запись первого геометрического условия в разомкнутом линейно-угловом ходе. Для правых углов поворота оно запишется так:
Сумма углов, подсчитанная по формулам (2.67) и (2.68), называется теоретической суммой углов хода. Сумма измеренных углов вследствие ошибок измерений, как правило, отличается от теоретической суммы на некоторую величину, называемую угловой невязкой и обозначаемую fβ:
Допустимое значение угловой невязки можно рассматривать как предельную ошибку суммы измеренных углов:
Используем известную формулу из теории ошибок для нахождения средней квадратической ошибки функции в виде суммы аргументов (раздел 1.11.2):
При После подстановки (2.72) в (2.70) получаем:
Для теодолитных ходов mβ = 30", поэтому:
Одним из этапов уравнивания является введение поправок в измеренные величины с целью приведения их в соответствие с геометрическими условиями. Обозначим поправку в измеренный угол Vβ и запишем условие:
откуда следует, что:
то-есть, поправки в углы следует выбрать так, чтобы их сумма была равна угловой невязке с противоположным знаком. В уравнении (2.75) n неизвестных, и для его решения необходимо наложить на поправки Vβ (n-1) дополнительных условий; наиболее простым вариантом таких условий будет:
то-есть, все поправки в измеренные углы одинаковы. В этом случае решение уравнения (2.75) получается в виде:
это означает, что угловая невязка fβ распределяется с обратным знаком поровну во все измеренные углы. Исправленные значения углов вычисляются по формуле:
По исправленным углам поворота вычисляют дирекционные углы всех сторон хода; совпадение вычисленного и заданного значений конечного исходного дирекционного угла является контролем прави льности обработки угловых измерений. Координатные условия. Решая последовательно прямую геодезическую задачу, вычислим приращения координат по каждой стороне хода ΔXi и ΔYi. Координаты пунктов хода получим по формулам:
Сложим эти равенства и получим для приращений ΔXi:
После приведения подобных имеем:
Аналогичная формула для суммы приращений ΔY имеет вид:
Получились еще два условия (2.80) и (2.81), которые называются координатными. Суммы приращений координат, подсчитанные по этим формулам, называются теоретическими суммами приращений. Вследствие ошибок измерения сторон и упрощенного способа распределения угловой невязки суммы вычисленных приращений координат в общем случае не будут равны теоретическим суммам; возникают так называемые координатные невязки хода:
по которым вычисляют абсолютную невязку хода:
и затем относительную невязку хода:
Уравнивание приращений ΔX и ΔY выполняют следующим образом. Сначала записывают суммы исправленных приращений:
и приравнивают их теоретическим суммам:
откуда следует, что:
В этих уравнениях по (n - 1) неизвестных и для их решения необходимо наложить на поправки VX и VY дополнительные условия. На практике поправки в приращения координат вычисляют по формулам:
которые соответствуют условию "поправки в приращения координат пропорциональны длинам сторон". Рассмотренный способ обработки измерений в линейно-угловом ходе можно назвать способом последовательного распределения невязок; строгое уравнивание линейно-углового хода выполняется по методу наименьших квадратов. После уравнивания одиночного линейно-углового хода ошибки положения его пунктов неодинаковы; они возрастают от начала и конца хода к его середине, и наибольшую ошибку положения имеет пункт в середине хода. В случае приближенного уравнивания эта ошибка оценивается половиной абсолютной невязки хода fs. При строгом уравнивании хода производится сплошная оценка точности, то-есть вычисляются ошибки положения каждого пункта хода, ошибки дирекционных углов всех сторон хода, а также ошибки уравненных значений углов и сторон хода.
|
||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.37.129 (0.007 с.) |

 (2.65)
(2.65) (2.66)
(2.66)

 (2.67)
(2.67) (2.68)
(2.68) (2.69)
(2.69) (2.70)
(2.70)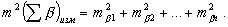 (2.71)
(2.71)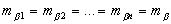

 (2.72)
(2.72)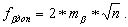 (2.73)
(2.73) (2.74)
(2.74)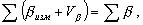
 (2.75)
(2.75) (2.76)
(2.76) (2.77)
(2.77)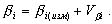 (2.78)
(2.78)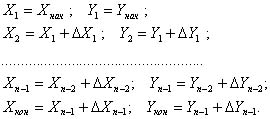 (2.79)
(2.79)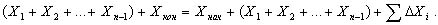

 (2.80)
(2.80)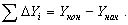 (2.81)
(2.81) (2.82)
(2.82) (2.83)
(2.83) (2.84)
(2.84)
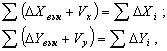
 (2.85)
(2.85)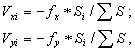 (2.91)
(2.91)


