
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конструктивные элементы геодезических измерительных приборовСодержание книги
Поиск на нашем сайте
Отсчетные приспособления Измерить какую-либо величину - значит сравнить ее с другой однородной величиной, принятой за единицу измерения. Приспособление, несущее единицу измерения, называется рабочей мерой. Обыкновенная линейка с делениями сантиметров и миллиметров, транспортир с делениями градусов - это примеры рабочих мер. Шкала рабочей меры как правило равномерна; она может располагаться по прямой линии, по дуге окружности или по какой-либо другой кривой. Отсчитывание по шкале рабочей меры производят по отсчетному индексу (начало и конец отрезка линии, сторона угла, штрих логарифмической линейки, стрелка весов и т.п.). В общем случае отсчетный индекс (на рис.3.1. - О.И.) устанавливается между двумя штрихами шкалы; один из них называют младшим штрихом (мл.), другой - старшим (ст.).
Рис.3.1
Отсчет N по шкале равен сумме двух величин: N = Nмл + x, (3.1) где Nмл - значение младшего штриха шкалы, Nмл = 55, Величину x можно получать разными способами, простейший из них - оценивание на глаз. Другой способ предполагает наличие специального отсчетного приспособления, назначение которого - измерять величину x с той или иной точностью. Известны следующие отсчетные приспособления: в машиностроении - нониус (верньер), микрометр, микроскоп-микрометр, в оптическом приборостроении, штриховой и шкаловой микроскопы, оптический микрометр и т.д. Верньер - одно из простейших отсчетных приспособлений. Его строят следующим образом: отрезок в n делений шкалы рабочей меры (основной шкалы) переносят на прилегающую поверхность и делят его там на (n + 1) равных частей, получая шкалу верньера (рис.3.2). Обозначим через λ цену деления основной шкалы и через μ - цену деления верньера; точностью верньера t называют разность t = λ - μ. (3.2) По построению λ * n = μ * (n + 1), поэтому
Подставив это выражение в формулу (3.2), получим
то-есть, точность верньера равна цене деления основной шкалы, деленной на число делений верньера.
Рис.3.2 Рис.3.3
В практике очень часто встречается верньер на одну десятую, когда n = 9; точность такого верньера равна одной десятой деления основной шкалы. Роль отсчетного индекса в верньере выполняет его нулевой штрих. Если он совмещен с каким-либо штрихом основной шкалы, то отсчет по основной шкале равен значению этого штриха. Все остальные штрихи верньера не совпадают со штрихами основной шкалы; первый штрих верньера отстоит от ближайшего штриха основной шкалы на величину λ - μ = t, второй штрих верньера отстоит от ближайшего штриха основной шкалы на 2*t, третий - на 3*t и т.д. Если сейчас сместить верньер относительно основной шкалы на величину t, то со штрихом основной шкалы совпадет 1-й штрих верньера; если сместить верньер на 2*t, то со штрихом основной шкалы совпадет 2-й штрих верньера и т.д. Если сместить верньер на величину k*t, то со штрихом основной шкалы совпадет k-й штрих верньера, поэтому формула отсчета N по верньеру имеет вид (рис.3.3) N = Nмл + k*t, (3.4) где: Nмл - отсчет по младшему штриху основной шкалы, Чтобы не умножать на t, верньер подписывают в единицах основной шкалы. Например, для угловой шкалы при t = 30" подпись первого штриха 30", подпись второго штриха 1' и т.д. Наблюдатель считывает с основной шкалы значение младшего штриха Nмл, находит на шкале верньера штрих, совпавший со штрихом лимба, и считывает его значение k*t; складываются эти два отсчета в уме. Оптические отсчетные приспобления рассмотрим на примере угловой шкалы, расположенной на окружности; такая шкала называется угломерным кругом или лимбом. Ценой деления лимба λ называют центральный угол, стягиваемый дугой в одно деление; в практике встречаются лимбы с ценой деления 1o, 20', 10', 5'. Диаметр лимбов бывает от 72 мм до 270 мм. Роль отсчетного индекса при отсчете по лимбу могут выполнять одиночный штрих, двойной штрих (биссектор), нулевой штрих шкалы отсчетного приспособления, штрих основной шкалы (шкалы лимба). Штриховой микроскоп. Отсчетным индексом в штриховом микроскопе является неподвижный штрих, выгравированный на стеклянной пластинке, помещенной на пути хода лучей, идущих от осветитель ного окошка через штрихи лимба в отсчетный микроскоп. Оценка доли деления лимба выполняется на глаз. Из опыта установлено, что при отсчитывании на глаз наибольшая точность достигается при видимом расстоянии между штрихами 2.00 мм и толщине штрихов 0.10 мм; при таких условиях ошибка отсчета составляет 0.1 деления. Рассчитаем, с какой точностью можно взять на глаз отсчет по лимбу диаметром d=100 мм и разделенному на 360 частей: цена одного деления равна 1o. Периметр кольца делений равен π*d=314 мм; длина дуги в 1o l = 314 мм/360 = 0.9 мм. Если бы длина деления была равна 2 мм, то ошибка 0.1 деления соответствовала бы ошибке отсчитывания по шкале лимба 6'; при длине деления 0.9 мм ошибка отсчитывания будет примерно в 2 раза больше. Такой точности для измерения углов недостаточно, поэтому поступают следующим обра зом: делят градус на более мелкие деления и рассматривают их че рез микроскоп. Например, при диаметре лимба 72 мм и количестве делений на нем 2160 одно деление лимба равно 10'; увеличение микроскопа равно 18x, следовательно, видимая длина одного деления равна l = π*72*18 мм/2160 = 1.93 мм, и ошибка отсчитывания по лимбу будет 1'. В поле зрения окуляра штрихового микроскопа видны деления лимба и отсчетный индекс - штрих; отсчет по горизонтальному кругу (Г) равен 69o47', по вертикальному (В) - 358o150' (рис.3.4).
Рис.3.4 Рис.3.5
Шкаловой микроскоп. На пути хода лучей от осветительного окошка через штрихи лимба в поле зрения микроскопа помещена стеклянная пластинка с гравированной шкалой. Длина шкалы равна длине одного деления лимба λ; шкала разделена на n равных частей, цена одного деления шкалы шкалового микроскопа обозначается буквой μ и равна μ = λ / n. Отсчетным индексом является нулевой штрих шкалы шкалового микроскопа. Доля деления лимба от младшего штриха шкалы лимба до отсчетного индекса измеряется непосредственно по шкале микроскопа, так как направления возрастания делений на лимбе и на шкале микроскопа противоположные (рис.3.5). Доля деления шкалы микроскопа оценивается на глаз. Полный отсчет по лимбу равен сумме отсчетов по младшему штриху лимба Nмл и по шкале микроскопа Nш: N = Nмл + Nш. (3.5) На рис.3.5 отсчет по лимбу (λ=1o, n=60, μ=1') равен N = 20o + 54.3' = 20o 54.3'. При отсчете по шкале оптического отсчетного приспособления может появиться ошибка, причиной которой является рен. Рен - это разность между номинальным n и фактическим n' количеством делений шкалы отсчетного устройства, укладывающихся в одном делении (или полуделении) лимба; рен отсчетного устройства обозначается буквой r. Если совместить нулевой штрих шкалы шкалового микроскопа с каким-либо штрихом шкалы лимба, то n-й штрих шкалы должен точно совпасть с соседним штрихом лимба (рис.3.6-а). Но из-за мелких погрешностей при сборке и юстировке оптической системы прибора этого может и не быть (рис.3.6-б). Значение рена просто считывается по положению штриха лимба; на рис.3.6-б r = 1.5'; для удобства определения рена за пределами шкалы обычно имеются по два дополнительных деления. При заметном несовпадении n-ного штриха со штрихом лимба (r > 0.1 деления шкалы микроскопа) прибор полагается сдать в мастерскую.
Рис.3.6 С конструкцией и принципом действия остальных отсчетных приспособлений можно ознакомиться в специальной литературе.
Зрительные трубы При многих геодезических измерениях приходится наблюдать далекие предметы или рассматривать очень мелкие деления. Разрешающая способность человеческого глаза ограничена; критический угол зрения у человека в среднем равен 60" (у разных людей он колеблется от 40" до 120"). Критическим углом называют предельный угол зрения, при котором две точки начинают сливаться в одну. Для увеличения угла зрения, когда он меньше критического значения, применяют различные оптические приспособления, одним из которых является зрительная труба. Зрительные трубы бывают астрономическими и земными. Астрономические трубы дают обратное, то-есть, перевернутое изображение предметов; земные трубы дают прямое изображение. В геодезических приборах чаще применяют астрономические трубы, так как они имеют более простое устройство и в них меньше потери света. По конструкции зрительные трубы бывают прямые и ломаные. Основными деталями зрительных труб являются линзы - стеклянные пластинки различной формы; линзы бывают собирательные и рассеивающие. Все собирательные линзы выпуклые: двояковыпуклые, плосковыпуклые, вогнутовыпуклые; все рассеивающие линзы вогнутые: двояковогнутые, плосковогнутые, выпукловогнутые. Линза имеет оптический центр; лучи, проходящие через него, не изменяют своего направления; все остальные лучи, проходя через линзу, испытывют преломление и изменяют свое первоначальное направление. Линия, соединяющая центры сферических поверхностей линзы, называется главной оптической осью линзы. По обе стороны от оптического центра на главной оптической оси есть точки, называемые главными фокусами линзы: передний фокус F и задний фокус F1. Расстояние от оптического центра до фокуса называется фокусным расстоянием. Если поместить в главный фокус точечный источник света, то лучи, пройдя через линзу, выйдут из нее пучком, параллельным главной оптической оси. И наоборот, пучок света, параллельный главной оптической оси, пройдя через линзу, собирается в точке главного фокуса. Плоскость, перпендикулярная главной оптической оси и проходящая через точку фокуса, называется фокальной плоскостью линзы. Для построения изображения предметов в линзе обычно используют три луча: луч, проходящий через оптический центр линзы, луч, идущий параллельно главной оптической оси, луч, проходящий через передний фокус линзы. Изображение считается действительным, если оно получается на пересечении лучей в прямом направлении; изображение считается мнимым, если оно получается на пересечении лучей в обратном направлении. Для всякой линзы справедлива формула:
где: a - расстояние от оптического центра до предмета, Ход лучей в трубе Кеплера. Астрономическая труба Кеплера является простейшей зрительной трубой; она состоит из двух собирательных линз - объектива и окуляра, имеющих общую главную оптическую ось, и корпуса; объектив трубы Кеплера - длиннофокусный, а окуляр - короткофокусный. При этом изображение, даваемое объективом, должно располагаться между передним фокусом окуляра и его оптическим центром; Построим в трубе Кеплера изображение отрезка BC, то-есть, нарисуем ход лучей от точек B и C, используя два из трех перечисленных выше лучей (рис.3.7).
Рис.3.7. Объектив дает действительное обратное уменьшенное изображение предмета - отрезок bc. Изображение, даваемое окуляром, - мнимое, обратное, увеличенное - отрезок b'c'. Сам окуляр дает прямое изображение, но поскольку оно уже было обратным, то обратным и остается. Под увеличением трубы понимают отношение угла зрения, под которым изображение предмета видно в трубе, к углу зрения, под которым предмет виден невооруженным глазом, то-есть, без трубы. Обозначим первый угол через α, а второй - через β и напишем формулу увеличения трубы V =α / β. (3.7) Из треугольника DF'1O2 имеем:
а из треугольника MO1F:
Углы α и β обычно малые, так как расстояние до предмета несравнимо больше размеров трубы, поэтому вместо тангенсов этих углов можно взять их значения в радианной мере: tg(α/2) = α/2 и tg(β/2) = β/2, откуда следует, что отношение углов α и β равно отношению тангенсов их половинных значений:
Подставим в эту формулу выражения тангенсов углов из (3.8) и (3.9) и получим:
Увеличение трубы Кеплера равно отношению фокусного расстояния объектива к фокусному расстоянию окуляра. Высокоточные геодезические приборы имеют сменные окуляры с разными фокусными расстояниями, и смена окуляра позволяет изменять увеличение трубы в зависимости от условий наблюдений. Определение увеличения зрительной трубы с помощью рейки. Если навести трубу на близкостоящую рейку,то можно сосчитать, сколько делений рейки N, видимой невооруженным глазом, соответствуют n делениям рейки, видимой в трубу. Для этого нужно смотреть поочередно в трубу и на рейку, проектируя деления рейки из поля зрения трубы на рейку, видимую невооруженным глазом. Обозначим через γ угол, под которым видны n делений в трубу и N делений без трубы (рис.3.8). Тогда одно деление рейки видно в трубу под углом: α = γ / n, а без трубы - под углом: β = γ / N.
Рис.3.8
Отсюда: V = N / n. Этот способ определения увеличения трубы называется способом Галилея. Увеличение трубы можно приближенно вычислить по формуле: V = D / d, (3.11) где D - входной диаметр объектива; Поле зрения трубы. Полем зрения трубы называют участок пространства, видимый в трубу при неподвижном ее положении. Поле зрения измеряют углом ε, вершина которого лежит в оптическом центре объектива, а стороны касаются краев отверстия диафрагмы (рис.3.9). Диафрагма диаметром d1 устанавливается внутри трубы в фокальной плоскости объектива.Из рисунка 3.11 видно, что:
откуда
Рис.3.9.
Обычно в геодезических приборах принимают d1 = 0.7 * fок, тогда в радианной мере: ε = 0.7 / V. Если ε выразить в градусах, то: ε = 40o / V. (3.12) Чем больше увеличение трубы, тем меньше ее угол зрения. Так, например, при V = 20x ε = 2o, а при V = 80x ε = 0.5o. Разрешающая способность трубы оценивается по формуле:
Например, при V = 20x ψ = 3"; под таким углом виден предмет размером 5 см на расстоянии 3.3 км; человеческий глаз может видеть этот предмет на расстоянии всего 170 м. Сетка нитей. Правильным наведением зрительной трубы на предмет считается такое, когда изображение предмета находится точно в центре поля зрения трубы. Чтобы исключить субъективный фактор при нахождении центра поля зрения, его обозначают сеткой нитей. Сетка нитей - это в простейшем случае два взаимно перпендикулярных штриха, нанесенных на стеклянную пластинку, которая крепится к диафрагме трубы. Сетка нитей бывает разных видов; на рис.3.10 показаны некоторые из них. Сетка нитей имеет исправительные винты: два боковых (горизонтальных) и два вертикальных. Линия, соединяющая центр сетки нитей и оптический центр объектива, называется визирной линией или визирной осью трубы.
Рис.3.10
Установка трубы по глазу и по предмету. При наведении трубы на предмет нужно одновременно четко видеть в окуляре сетку нитей и изображение предмета. Установкой трубы по глазу добиваются четкого изображения сетки нитей; для этого передвигают окуляр относительно сетки нитей, вращая рифленое кольцо на окуляре. Установка трубы по предмету называется фокусированием трубы. Расстояние до рассматриваемых предметов бывает разным, и согласно формуле (3.6) при изменении a расстояние b до его изображения также меняется. Чтобы изображение предмета при рассматривании его в окуляр было четким, оно должно располагаться в плоскости сетки нитей. Передвигая окулярную часть трубы вдоль главной оптической оси, изменяют расстояние от сетки нитей до объектива до тех пор, пока оно станет равным b. Трубы, у которых фокусирование выполняется путем изменения расстояния между объективом и сеткой нитей, называются трубами с внешней фокусировкой. Такие трубы имеют большую и притом переменную длину; они негерметичны, поэтому внутрь них попадают пыль и влага; на близкие предметы они вообще не фокусируются. Зрительные трубы с внешней фокусировкой в современных измерительных приборах не применяются Более совершенными являются трубы с внутренней фокусировкой (рис.3.11); в них применяется дополнительная подвижная рассеивающая линза L2, образующая вместе с объективом L1 эквивалентную линзу L. При перемещении линзы L2 изменяется расстояние между линзами l и, следовательно, изменяется фокусное расстояние f эквивалентной линзы. Изображение предмета, находящееся в фокальной плоскости линзы L, также перемещается вдоль оптической оси, и когда оно попадает на плоскость сетки нитей становится четко видным в окуляре трубы. Трубы с внутренней фокусировкой короче; они герметичны и позволяют наблюдать близкие предметы;в современных измерительных приборах применяются в основном такие зрительные трубы.
Уровни Уровни служат для приведения осей прибора в вертикальное или горизонтальное положение и для измерения малых углов наклона. Применение уровней основано на свойстве пузырька газа занимать в жидкости наивысшее положение. Уровни бывают цилиндрические и круглые. Цилиндрический уровень состоит из чувствительного элемента - ампулы и металлической оправы для ее крепления и защиты от внешних воздействий. Ампула цилиндрического уровня - это стеклянная трубка, запаянная с обоих концов и заполненная спиртом или серным эфиром; небольшое пространство занимают пары этой жидкости, оно называется пузырьком уровня. Ампула имеет форму дуги большого радиуса; касательная к дуге в середине пузырька всегда горизонтальна, так как выталкивающая сила, действующая на пузырек, направлена по вертикальной линии (пузырек принимает форму дуги окружности, выталкивающая сила на правлена по радиусу дуги, касательная перпендикулярна радиусу). На ампуле нанесены деления, на точных уровнях деления подписаны. Ценой деления уровня t называется центральный угол, соответствующий дуге в одно деление шкалы на ампуле. Точка O в середине шкалы называется нульпунктом уровня, а касательная, проведенная в нульпункте, называется осью цилиндрического уровня U-U (рис.3. 12). Если пузырек находится в нульпункте, то ось уровня занимает горизонтальное положение. Если пузырек уровня находится не в нульпункте, то ось уровня занимает наклонное положение. Чтобы приводить какую-либо линию или плоскость в горизонтальное положение, нужно закрепить уровень так, чтобы ось уровня была строго параллельной искомой линии или плоскости. Чтобы приводить линию или плоскость в вертикальное положение, нужно закрепить уровень так, чтобы ось уровня была строго перпендикулярна искомой линии или плоскости. Без выполнения этих условий применение уровня не имеет смысла.
Рис.3.12 Если же условия выполняются, то при положении пузырька уровня в нульпункте ось уровня займет горизонтальное положение, а искомая линия или плоскость - горизонтальное положение в первом случае и вертикальное положение во втором случае. Внутренняя поверхность ампулы имеет форму, получающуюся при вращении дуги AB радиуса R вокруг хорды AB (рис.3.12). Радиус дуги R вычисляют по расчетной цене деления τ. Обозначив через l длину одного деления шкалы на ампуле, напишем формулу для длины дуги в функции центрального угла:
откуда
При τ = 10", l = 2 мм и ρ = 206265" получим R = 41 м. При наклоне уровня на угол ε пузырек отклонится от нульпункта на n деления, то-есть, ε = n * τ. (3.15) Отсюда следует второе определение цены деления уровня: цена деления уровня - это угол, на который наклонится ось уровня при смещении пузырька на одно деление шкалы. Определение цены деления уровня по рейке. Из формулы (3.15) следует, что: τ = ε / n, т.е. для определения цены деления нужно знать угол ε и сосчитать число делений, на которое сместится пузырек (рис.3.13). Угол наклона ε можно определить разными методами, например, с помощью рейки. Наведем трубу на рейку и возьмем отсчеты: по рейке - b1 и по уровню.
Рис.3.13
Затем немного наклоним трубу и снова возьмем отсчеты: по рейке - b2 и по уровню. Угол наклона ε вычисляется по формуле:
где S - расстояние от нивелира до рейке. Число делений уровня n, на которое переместился пузырек, подсчитывают по разности отсчетов по уровню при первом и втором наведениях на рейку. Более точное определение цены деления уровня производят на специальном устройстве - экзаменаторе; при этом одновременно выполняют исследование качества шлифовки внутренней поверхности ампулы уровня. По конструкции цилиндрические уровни бывают простыми, компенсированными и камерными. У простых уровней ампула заполнена жидкостью и имеет один пузырек. У компенсированных уровней внутри ампулы помещена стеклянная трубка с запаянными концами. При изменении температуры объемы жидкости и пузырька газа изменяются неодинаково вследствие разных коэффициентов расширения. Это приводит к тому, что при понижении температуры пузырек удлиняется, при повышении - укорачивается. Наличие стеклянной трубки в ампуле уменьшает объем жидкости, и поэтому влияние изменения температуры на длину пузырька ослабляется. У камерных уровней внутри ампулы есть перегородка с отверстием внизу, которая делит ампулу на две камеры - основную и запасную. Запасная камера намного меньше по объему, и в ней помещается запасной пузырек. При изменении длины основного пузырька наклоняют уровень и либо убирают часть пузырька в запасную камеру, либо добавляют некоторое количество газа из запасной камеры. Согласно Инструкции [18] длина пузырька должна составлять 0.4 - 0.5 длины шкалы на ампуле. По точности уровни бывают малой точности (τ > 1'), средней точности (5" < τ < 1') и высокой точности (τ < 5"). Цилиндрические уровни имеют цену деления меньше 1'. Круглый уровень - это часть стеклянной сферы, на которую нанесены концентрические окружности. Центр окружностей является нульпунктом круглого уровня. Осью круглого уровня называется нормаль к сферической поверхности ампулы, проведенная в нульпункте. Если пузырек уровня находится в нульпункте, то его ось занимает вертикальное (отвесное) положение. Круглые уровни относятся к уровням малой точности. Поверка установки цилиндрического уровня. Пусть цилиндрический уровень предназначен для приведения в вертикальной положение оси вращения геодезического прибора; тогда условие их взаимного положения читается так: ось уровня должна быть перпендикулярна оси вращения прибора.Теоретическое положение оси уровня и оси вращения прибора изображено на рис.3.14; на нем UU1 - ось уровня, ZZ1 - ось вращения прибора, она вертикальна и составляет с осью уровня угол 90o; пузырек уровня находится в нульпункте. При повороте прибора вокруг своей оси ось уровня описывает в пространстве горизонтальную плоскость, и после поворота прибора на 180o пузырек остается в нульпункте.
Рис.3.14
Пусть угол между осью уровня и осью вращения прибора равен не точно 90o, а (90o - i) (рис.3.15). Если установить прибор так, чтобы пузырек уровня был в нульпункте, то ось уровня займет горизонтальное положение, а ось вращения прибора будет наклонена на угол i относительно своего правильного положения. Задача поверки - найти угол i и устранить его. Повернем прибор на 180o (рис.3.16). Ось уровня опишет коническую поверхность с углом при вершине конуса 180o-2i и займет не горизонтальное положение, а наклонится относительно горизонта на угол 2i; пузырек отклонится от нульпункта на n делений, следовательно, 2 * i = n * τ, откуда
Рис.3.15 Рис.3.16
Чтобы условие выполнялось, нужно, во-первых, изменить угол между осью уровня и осью вращения прибора на величину i и, во-вторых, наклонить прибор также на угол i. Практически поступают так: сначала подъемными винтами наклоняют прибор на угол i; при этом пузырек должен приблизиться к нульпункту на половину отклонения. Затем, пользуясь исправительными винтами уровня, изменяют положение ампулы в корпусе прибора; при этом пузырек должен установиться точно в нульпункте. Таким образом, последовательность действий при поверке установки уровня следующая: Вращая прибор, установить уровень параллельно двум подъемным винтам. Этими подъемными винтами привести пузырек уровня в нульпункт. Повернуть прибор точно на 180o. Сосчитать количество делений n отклонения пузырька уровня от нульпункта. Подъемными винтами сместить пузырек обратно на n/2 делений. Исправительными винтами уровня привести пузырек в нульпункт. Если угол i большой, то после поворота прибора на 180o пузырек уходит за пределы шкалы, и количество делений n сосчитать нельзя. В этом случае отклонение пузырька от нульпункта можно измерить в более крупных единицах, например, в оборотах подъемных винтов, и исправлять уровень способом последовательных приближений. Существуют и другие способы исправления уровня; один из них - способ Г.Лысова - позволяет исправить сильно разъюстированный уровень за одно приближение. Последовательность операций в способе Г.Лысова. Умеренно вывернуть (или завернуть) любой из подъемных винтов, чтобы наклон прибора был заметен глазом (i> 1o). Плавно вращая прибор, зафиксировать такое его положение, при котором пузырек уровня находится точно в нульпункте; взять отсчет по горизонтальному лимбу N1. Плавно вращая прибор, зафиксировать второе его положение, при котором пузырек уровня также находится точно в нульпункте; взять отсчет по горизонтальному лимбу N2. Вычислить отсчет N = 0.5 (N1 + N2) + 90o и, плавно вращая прибор, установить его на горизонтальном лимбе. Исправительными винтами уровня привести пузырек в нульпункт.
|
||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 579; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.27.154 (0.011 с.) |



 (3.3)
(3.3)


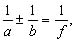 (3.6)
(3.6)
 (3.8)
(3.8) (3.9)
(3.9)
 (3.10)
(3.10)



 (3.13)
(3.13)
 Рис.3.11
Рис.3.11

 (3.14)
(3.14)







