
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямая геодезическая задача на плоскостиСодержание книги
Поиск на нашем сайте
В геодезии есть две стандартные задачи: прямая геодезичеcкая задача на плоскости и обратная геодезическая задача на плоскости. Прямая геодезическая задача - это вычисление координат X2, Y2 второго пункта, если известны координаты X1, Y1 первого пункта, дирекционный угол α и длина S линии, соединяющей эти пункты. Прямая геодезическая задача является частью полярной засечки, и формулы для ее решения берутся из набора формул (2.7):
Обратная геодезическая задача на плоскости Обратная геодезическая задача - это вычисление дирекционного угла α и длины S линии, соединяющей два пункта с известными координатами X1, Y1 и X2, Y2 (рис.2.5).
Рис.2.5
Построим на отрезке 1-2 как на гипотенузе прямоугольный треугольник с катетами, параллельными осям координат. В этом треугольнике гипотенуза равна S, катеты равны приращениям координат точек 1 и 2 (ΔX = X2 - X1, ΔY = Y2 - Y1), а один из острых углов равен румбу r линии 1-2. Если Δ X
Для данного рисунка направление линии 1-2 находится во второй четверти, поэтому на основании (1.22) находим:
Общий порядок нахождения дирекционного угла линии 1-2 включает две операции: определение номера четверти по знакам приращений координат Δ>X и ΔY (рис.1.4-а), вычисление α по формулам связи (1.22) в соответствии с номером четверти. Контролем правильности вычислений является выполнение равенства:
Если ΔX = 0.0, то S = іΔYі; Если ΔY = 0.0, то S = іΔXі Для решения обратной задачи в автоматическом режиме (в программах для ЭВМ) используется другой алгоритм, не содержащий тангенса угла и исключающий возможное деление на ноль:
если ΔY => 0o, то α = a,
Прямая угловая засечка Сначала рассмотрим так называемый общий случай прямой угловой засечки, когда углы β1 и β2 измеряются на двух пунктах с известными координатами, каждый от своего направления с известным дирекционным углом (рис.2.6).
Рис.2.6
Исходные данные: XA, YA, αAC, Измеряемые элементы: β 1, β2 Неизвестные элементы: X, Y Если αAC и αBD не заданы явно, нужно решить обратную геодезическую задачу сначала между пунктами A и C и затем между пунктами B и D. Графическое решение. От направления AC отложить с помощью транспортира угол β1 и провести прямую линию AP; от направления BD отложить угол β2 и провести прямую линию BP; точка пересечения этих прямых является искомой точкой P.
Аналитическое решение. Приведем алгоритм варианта, соответствующий общему случаю засечки: вычислить дирекционные углы линий AP и BP
написать два уравнения прямых линий для линии AP Y - YA= tgα1 * (X - XA), для линии BP Y - YB= tgα2 * (X - XB) (2.16) решить систему двух уравнений и вычислить неизвестные координаты X и Y:
Частным случаем прямой угловой засечки считают тот случай, когда углы β1 и β2 измерены от направлений AB и BA, причем угол β1 - правый, а угол β2 - левый (в общем случае засечки оба угла - левые) - рис.2.7.
Рис.2.7
Решение прямой угловой засечки методом треугольника соответствует частному случаю засечки. Порядок решения при этом будет такой: решить обратную задачу между пунктами A и B и получить дирекционный угол αAB и длину b линии AB, вычислить угол γ при вершине P, называемый углом засечки,
используя теорему синусов для треугольника APB:
вычислить длины сторон AP (S1) и BP (S2), вычислить дирекционные углы α1 и α2:
решить прямую задачу от пункта A к точке P и для контроля - от пункта B к точке P. Для вычисления координат X и Y в частном случае прямой угловой засечки можно использовать формулы Юнга:
От общего случая прямой угловой засечки нетрудно перейти к частному случаю; для этого нужно сначала решить обратную геодезическую задачу между пунктами A и B и получить дирекционный угол αAB линии AB и затем вычислить углы в треугольнике APB при вершинах A и B
Для машинного счета все рассмотренные способы решения прямой угловой засечки по разным причинам неудобны. Один из возможных алгоритмов решения общего случая засечки на ЭВМ предусматривает следующие действия: вычисление дирекционных углов α1 и α2, введение местной системы координат X'O'Y' с началом в пункте A и с осью O'X', направленной вдоль линии AP, и пересчет координат пунктов A и B и дирекционных углов α1 и α2 из системы XOY в систему X'O'Y' (рис.2.8): X'A = 0, Y'A = 0,
запись уравнений линий AP и BP в системе X'O'Y':
Рис.2.8
и совместное решение этих уравнений:
перевод координат X' и Y' из системы X'O'Y' в систему XOY:
Так как Ctgα2' = - Ctgγ и угол засечки γ всегда больше 0о, то решение (2.27) всегда существует.
Линейная засечка От пункта A с известными координатами XA, YA измерено расстояние S1 до определяемой точки P, а от пункта B с известными координатами XB, YB измерено расстояние S2 до точки P. Графическое решение. Проведем вокруг пункта A окружность радиусом S1 (в масштабе чертежа), а вокруг пункта B - окружность радиусом S2; точка пересечения окружностей является искомой точкой; задача имеет два решения, так как две окружности пересекаются в двух точках (рис.2.9). Исходные данные: XA, YA, XB, YB, Измеряемые элементы: S1, S2, Неизвестные элементы: X, Y. Аналитическое решение. Рассмотрим два алгоритма аналитического решения, один - для ручного счета (по способу треугольника) и один - для машинного счета.
Рис.2.9
Алгоритм ручного счета состоит из следующих действий: решение обратной геодезической задачи между пунктами A и B и получение дирекционного угла αAB и длины b линии AB, вычисление в треугольнике ABP углов β1 и β2 по теореме косинусов:
вычисление угла засечки γ
вычисление дирекционных углов сторон AP и BP: пункт P справа от линии AB
пункт P слева от линии АВ
решение прямых геодезических задач из пункта A на пункт P и из пункта B на пункт P: 1-е решение
2-е решение
Результаты обоих решений должны совпадать. Алгоритм машинного решения линейной засечки состоит из следующих действий: решение обратной геодезической задачи между пунктами A и B и получение дирекционного угла αAB и длины b линии AB, введение местной системы координат X'O'Y' с началом в точке A и осью O'X', направленной вдоль линии AB, и пересчет координат пунктов A и B из системы XOY в систему X'O'Y':
запись уравнений окружностей в системе X'O'Y':
и совместное решение этих уравнений, которое предусматривает раскрытие скобок во втором уравнении и вычитание второго уравнения из первого:
откуда
и
Если искомая точка находится слева от линии AB, то в формуле (2.39) берется знак "-", если справа, то "+". пересчет координат X' и Y' точки P из системы X'O'Y' в систему XOY по формулам (2.2):
Обратная угловая засечка К элементарным измерениям относится и измерение угла β на определяемой точке P между направлениями на два пункта A и B с известными координатами XA, YA и XB, YB (рис.2.10). Однако, это измерение оказывается теоретически довольно сложным, поэтому рассмотрим его отдельно. Проведем окружность через три точки A, B и P. Из школьного курса геометрии известно, что угол с вершиной на окружности измеряется половиной дуги, на которую он опирается. Центральный угол, опирающийся на ту же дугу, измеряется всей дугой, следовательно, он будет равен 2β (рис.2.10).
Рис.2.10
Расстояние b между пунктами A и B считается известным, и из прямоугольного треугольника FCB можно найти радиус R окружности:
Уравнение окружности имеет вид:
где XC и YC - координаты центра окружности. Их можно вычислить, решив либо прямую угловую, либо линейную засечку с пунктов A и B на точку C. В уравнении (2.42) X и Y - координаты любой точки окружности, в том числе и точки P, но для нахождения двух координат точки P одного такого уравнения недостаточно. Обратной угловой засечкой называют способ определения координат точки P по двум углам β1 и β2, измеренным на определяемой точке P между направлениями на три пункта с известными координатами A, B, C (рис.2.11). Графическое решение. Приведем способ Болотова графического решения обратной угловой засечки. На листе прозрачной бумаги (кальки) нужно построить углы β1 и β2 с общей вершиной P; затем наложить кальку на чертеж и, перемещая ее, добиться, чтобы направления углов на кальке проходили через пункты A, B, C на чертеже; переколоть точку P с кальки на чертеж. Исходные данные: XA, YA, XB, Измеряемые элементы: β1, β2. Неизвестные элементы: X, Y.
Рис.2.11
Аналитическое решение. Аналитическое решение обратной угловой засечки предусматривает ее разложение на более простые задачи, например, на 2 прямых угловых засечки и одну линейную, или на 3 линейных засечки и т.д. Известно более 10-ти способов аналитического решения, но мы рассмотрим только один - через последовательное решение трех линейных засечек. Предположим, что положение точки P известно, и проведем две окружности: одну радиусом R1 через точки A, B и P и другую радиусом R2 через точки B, C и P (рис.2.11). Радиусы этих окружностей получим по формуле (2.41):
Если координаты центров окружностей - точек O1 и O2 будут известны, то координаты точки P можно определить по формулам линейной засечки: из точки O1 по расстоянию R1 и из точки O2 - по расстоянию R2. Координаты центра O1 можно найти по формулам линейной засечки из точек A и B по расстояниям R1, причем из двух решений нужно взять то, которое соответствует величине угла β1: если β1<90o, то точка O1 находится справа от линии AB, если β1>90o, то точка O1 находится слева от линии AB. Координаты центра O2 находятся по формулам линейной засечки из точек B и C по расстояниям R2, и одно решение из двух возможных выбирается по тому же правилу: если β2<90o, то точка O2 находится справа от линии BC, если β2>90o, то точка O2 находится слева от линии BC. Задача не имеет решения, если все четыре точки A, B, C и P находятся на одной окружности, так как обе окружности сливаются в одну, и точек их пересечения не существует.
Комбинированные засечки В рассмотренных способах решения засечек количество измерений принималось теоретически минимальным (два измерения), обеспечивающим получение результата. На практике для нахождения координат X и Y одной точки, как правило, выполняют не два, а три и более измерений расстояний и углов, причем эти измерения выполняются как на исходных пунктах, так и на определяемых; такие засечки называются комбинированными. Понятно, что в этом случае появляется возможность контроля измерений, и, кроме того, повышается точность решения задачи. Каждое измерение, вводимое в задачу сверх теоретически минимального количества, называют избыточным; оно порождает одно дополнительное решение. Геодезические засечки без избыточных измерений принято называть однократными, а засечки с избыточными измерениями - многократными. При наличии избыточных измерений вычисление неизвестных выполняют методом уравнивания. Алгоритмы строгого уравнивания многократных засечек применяются при автоматизированном счете на ЭВМ; для ручного счета используют упрощенные способы уравнивания. Упрощенный способ уравнивания какой-либо многократной засечки (n измерений) предусматривает сначала формирование и решение всех возможных вариантов независимых однократных засечек (их число равно n-1), а затем - вычисление средних значений координат точки из всех полученных результатов, если они различаются между собой на допустимую величину.
Ошибка положения точки В одномерном пространстве (на линии) положение точки фиксируется значением одной координаты X, и ошибка положения точки Mp равна средней квадратической ошибке mx этой координаты. Истинное положение точки может находиться в интервале (X - t * mx) - (X + t * mx), то-есть, в обе стороны от значения X; на практике коэффициент t обычно задают равным 2.0 или 2.50. В двумерном пространстве (на поверхности) положение точки фиксируется значениями двух координат, и ошибка положения точки должна задаваться двумя величинами: направлением и ошибкой положения по этому направлению. Геометрическая фигура, внутри которой находится истинное положение точки, может иметь разную форму; в частном случае, когда ошибка положения точки по всем направлениям одинакова, получается круг радиуса R = Mp. Положение точки по двум измерениям получается в пересечении двух линий положения. Для измеренного расстояния S линией положения является окружность радиуса S с центром в исходной пункте A (рис.2.12а); для измеренного угла β с вершиной в исходном пункте A - прямая линия, проведенная под углом β к исходной линии AB (рис.2.12б). Вследствие ошибок измерений необходимо ввести понятие "полоса положения". Для расстояния S, измеренного со средней квадратической ошибкой ms - это круговой пояс (кольцо) шириной 2 * ms между двумя окружностями радиусами (S - ms) и (S + ms); для угла β, измеренного с ошибкой mβ - это узкий треугольник с вершиной в точке A и углом при вершине 2 * mβ. Линия положения точки является осью симметрии полосы положения (рис.2.12).
Рис.2.12. Линия положения и "полоса положения" точки P:
Введем понятие "вектор ошибки измерения" и обозначим его через V. Для измеренного расстояния вектор Vs направлен вдоль линии AP (прямо или обратно) и имеет модуль vs = ms; для измеренного угла вектор Vβ направлен перпендикулярно линии AP (влево или вправо от нее) и имеет модуль νβ = S * mβ / ρ, где S = A * P. Точка P, находясь на пересечении двух линий положения, является центром 4-угольника положения, образующегося в пересечении двух полос положения (рис.2.13).
Рис.2.13. 4-угольник положения: а) в линейной засечке, б) в прямой угловой засечке,
Этот элементарный 4-угольник можно считать параллелограммом, так как в пределах него дуги окружностей можно заменить отрезками касательных, а расходящиеся стороны угла - отрезками прямых, параллельных линии положения. Расстояния от точки P до границ 4-угольника неодинаковы, что говорит о различии ошибок положения точки P по разным направлениям. Линии положения делят 4-угольник положения на 4 равные части (рис.2.14-а), которые назовем параллелограммами ошибок с углами при вершинах γ и (180o - γ), где γ(180o - γ) - угол между векторами ошибок V1 и V2. Поскольку высоты параллелограммов ошибок численно равны модулям векторов ν1 и ν2, то стороны параллелограммов получаются по известным формулам (рис.2.14-а):
Рис.2.14
По известным сторонам параллелограмма ошибок и углу между ними γ(180o - γ) можно вычислить длину обоих его диагоналей: короткой - d1 и длинной - d2:
Таким образом, ошибка положения точки по шести направлениям (рис.2.14) выражается простыми формулами; для всех остальных направлений формулы будут более сложные. Для обобщенной характеристики точности определения точки P нужно иметь некоторое усредненное значение ошибки положения точки P, которое можно вычислить: как радиус круга R, площадь которого (π * R2) равна площади параллелограмма положения точки P (4 * a * b * Sinγ),
как ошибку положения по "наиболее слабому направлению", совпадающему с направлением длинной диагонали:
как среднее квадратическое из длинной и короткой диагоналей параллелограмма ошибок:
На практике чаще других применяется третий вариант, в котором легко получаются формулы для оценки точности любой однократной засечки: полярная засечка (рис.2.4):
прямая угловая засечка (рис.2.6, 2.7):
линейная засечка (рис.2.9):
обратная угловая засечка (рис.2.11). В этой засечке правая часть формулы ошибки положения точки P должна содержать три слагаемых: ошибку линейной засечки точки О1 с исходных пунктов A и B (mO1), ошибку линейной засечки точки О2 с исходных пунктов B и C (mO2), ошибку линейной засечки точки P с точек О1 и О2 (mP),
Угол засечки γ зависит от взаимного расположения линий BC и BA и углов β1 и β2; для рис.2.11 этот угол вычисляется по формуле:
Для многих случаев практики достаточно считать, что истинное положение точки P находится внутри круга радиуса MP с центром в точке P. В строгой теории рассмотренный критерий называется радиальной ошибкой. Кроме того, в этой теории применяются и более сложные критерии, такие как "эллипс ошибок" (кривая 2-го порядка), "подера эллипса ошибок" (кривая 4-го порядка) и др. [22]. При количестве измерений n>2 (многократные засечки) точка P получается в пересечении n линий положения, соответствующих уравненным значениям измерений; полосы положения, пересекаясь, образуют 2 * n-угольник (рис.2.14-б). Наибольшая ошибка положения точки P будет определяться расстоянием от точки P до самой удаленной от нее вершины этого многоугольника. Из рисунка 2.14-б понятна роль третьего измерения в уменьшении ошибки положения точки P; кстати, на этом рисунке второе измерение практически не влияет на значение ошибки положения точки.
|
||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 1203; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.41.109 (0.007 с.) |

 (2.8)
(2.8)
 00 и Δ Y
00 и Δ Y  (2.9)
(2.9) (2.10)
(2.10) (2.11)
(2.11) (2.12)
(2.12) (2.13)
(2.13)
 (2.14),
(2.14), (2.15)
(2.15) (2.17),
(2.17), (2.18)
(2.18)
 (2.19)
(2.19) (2.20)
(2.20) (2.21)
(2.21) (2.22)
(2.22) BAP = αAB - (αAC + β1) и
BAP = αAB - (αAC + β1) и  (2.23),
(2.23),  (2.24),
(2.24), (2.26)
(2.26)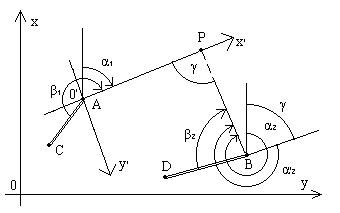
 (2.27)
(2.27) (2.28)
(2.28)
 (2.29)
(2.29) (2.30)
(2.30)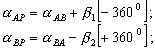 (2.31)
(2.31) (2.32)
(2.32) (2.33)
(2.33) (2.34)
(2.34) (2.35)
(2.35)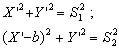 (2.36)
(2.36) (2.37)
(2.37) (2.38)
(2.38) (2.39)
(2.39)

 (2.41)
(2.41) (2.42)
(2.42)
 (2.43)
(2.43)

 (2.44)
(2.44)
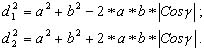
 (2.45)
(2.45) (2.46)
(2.46) (2.47)
(2.47) (2.48)
(2.48) (2.49)
(2.49) (2.50)
(2.50) (2.50a)
(2.50a) (2.51)
(2.51)


