
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Привязочные работы в полигонометрииСодержание книги
Поиск на нашем сайте Значение и виды привязок. Общие положения. Привязка – это особый вид работ, позволяющий получить в процессе измерений дирекционный угол, расстояние или координаты определяемой точки по отношению к пунктам государственной геодезической сети (ГГС). Привязку к пунктам геодезической сети можно произвести различными способами в зависимости от расположения этих пунктов по отношению к определяемым точкам.
Наиболее простая привязка - это непосредственное примыкание хода к пунктам ГГС более высокого класса, с возможностью измерения примычных углов между пунктами ГГС и сторонами полигонометрического хода (в дальнейшем будем называть такой вид привязки - азимутальная).
Если имеется возможность непосредственной привязки хода к пунктам ГГС, но отсутствует возможность выполнить измерения примычных углов (утеряны ориентирные пункты, нет прямой видимости между пунктами ГГС), то такую привязку будем называть координатной. Если непосредственная привязка к пункту ГГС невозможна, то в этом случае используют особые способы привязок, позволяющие определить неизвестные параметры (координаты, расстояния, дирекционные углы, высоты). Такие измерения, выполняемые для определения отдельных координат точек местности с использованием пунктов геосети, называют засечками.
В привязочных работах очень часто приходится определять неприступные расстояния. Для этого используют стандартные построения и математические зависимости известные из тригонометрии – теоремы синусов и косинусов.
Для вычисления дирекционных углов и расстояний практически всегда используется обратная геодезическая задача, для определения приращений координат – прямая геодезическая задача.
Непосредственная привязка к пунктам ГГС Самым простым способом привязки является непосредственное примыкание теодолитного или полигонометрического хода к пунктам триангуляции или полигонометрии высшего класса с возможностью измерения примычных углов (азимутальная привязка).
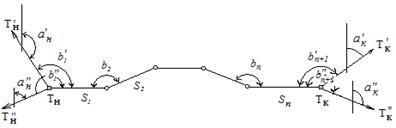
рис. 4 Если известны координаты пунктов Тн и Тк (рис. 4), из которых видны пункты государственной геодезической сети
Далее, дирекционные углы передаются на стороны хода обычным порядком, по известному алгоритму. После чего ход уравнивается (вычисляются рабочие координаты).
Пример вычисления рабочих координат полигонометрического хода с непосредственной привязкой к пунктам геосети (азимутальная привязка).
В ряде случаев ход не удается привязать к исходным направлениям. Например, когда на исходном пункте отсутствует видимость с земли на соседние пункты, наружные знаки пришли в ветхость, а центры на ориентирных пунктах потеряны. В таких случаях используют особые способы привязки.
Координатная привязка Возможны два варианта координатной привязки:
Вариант 1.
Предположим, что от пункта полигонометрии пп1 необходимо проложить ход (пп1,р1,р2 … и т.д.). Однако, в силу каких либо причин (построили дом, вырос лес и т.д.) видимость с пункта пп1 на пункт пп2 отсутствует. Выполнить непосредственную привязку (измерить примычный угол β1) не представляется возможным. В данном случае выполняется простейшая линейно-угловая засечка, в результате решения которой, аналитически вычисляется примычный угол β1 на точку хода. Для решения данной задачи, на пункты пп1 и пп2 устанавливаются штативы с визирными целями. На местности, выбирается точка хода р1, с которой имеется прямая видимость на пункт привязки пп1 и пункт ориентирования пп2. Точка р1 закрепляется на местности. Над точкой устанавливается прибор – теодолит или тахеометр – и измеряются:
Решение засечки сводится к решению треугольника р1пп1пп2, из которого находится угол β1. Для решения треугольника используется теорема синусов.
Для решения треугольника с использованием теоремы синусов необходимо определить расстояние L, между исходным пунктом пп1 и пунктом ориентирования пп2. Возможны два случая:
Вычислив L, используем теорему синусов для вычисления углов β1 и контрольного угла ε.
Из данного выражения находим угол β1:
Для контроля находят угол ε:
Контролем правильности вычислений служит известное из геометрии соотношение – сумма углов треугольника равна 180º или
где δ - предельная СКП измерения угла прибора, которым измерен угол φ.
Вариант 2. (координатная привязка) Имеются исходные пункты, но отсутствуют пункты ориентирования. Теория координатной привязки достаточно проста. Предположим, что через центр круга (рис. 5), радиусом R, проходит система координат XY. Радиус R1 в системе координат XY проведен под углом a и имеет приращения координат Dx1 и Dy1.
Рис 5 А радиус R1’ в той же системе координат XY проведен под углом a’ и имеет приращения координат Dx1’ и Dy1’. Несмотря на то, что сами приращения координат изменяются с изменением a, радиус данной окружности остается постоянным: R1= R1’ Используя теорему Пифагора можно записать
Для вычисления приращений координат радиусов R1 и R1’ используем прямую геодезическую задачу:
Dx1= Rcos(a); Dy1= Rsin(a); Dx1’ = R’cos(a’); Dy1’ = R’sin(a’);\ Для того, чтобы через радиус R’ вычислить приращения координат радиуса R, R’ необходимо довернуть на угол da = a - a¢ и тогда приращения координат будут одни и те же.
Dx1 = R’cos(a’ + da); Dy1 = R’sin(a’ + da); Алгоритм решения задачи. Предположим, что между двумя твердыми пунктами Т1 и Т2 проложили ход с координатной привязкой. (рис. 6) Необходимо вычислить координаты поворотных точек в системе координат ГГС.
Рис. 6
Исходя из изложенного, предположим, что пункт Т1 начало вектора R1, а пункт Т2 его конец. Задача решается в два приближения.
Первое приближение.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 3742; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.007 с.) |

 ,
,  ,
, 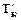 ,
, 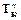 , то на пункте Тн необходимо измерить примычные углы b’1 и b’’, а на пункте Тк — углы b’ n+1 и b’’n+1. Вычислив по координатам пунктов Тн,
, то на пункте Тн необходимо измерить примычные углы b’1 и b’’, а на пункте Тк — углы b’ n+1 и b’’n+1. Вычислив по координатам пунктов Тн, 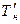 ,
, 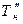 , Тк,
, Тк,  ,
, 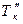 дирекционные углы
дирекционные углы 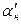 ,
, 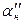 ,
, 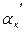 ,
,  сторон
сторон 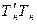 ,
, 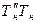 ,
,  ,
, 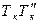 (обратная геодезическая задача), можно передать дирекционные углы на стороны хода S1 и Sn. Этот способ привязки дает надежный контроль, так как разность примычных углов
(обратная геодезическая задача), можно передать дирекционные углы на стороны хода S1 и Sn. Этот способ привязки дает надежный контроль, так как разность примычных углов 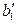 и
и  ,
,  и
и 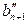 должна равняться разности дирекционных углов
должна равняться разности дирекционных углов 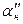 ,
, 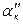 и
и 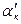 .
.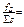



 ;
; .
. .
. .
. .
.







