
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные характеристики полигонометрии I и 2 разрядовСодержание книги
Поиск на нашем сайте Полигонометрия. 1 Плановые государственные геодезические сети. ( Общие положения ) Геодезическими сетями принято называть аналитические линейно-угловые построения на земной поверхности, закрепленные на местности, пункты которых имеют координаты, вычисленные в определенной системе координат по результатам угловых и линейных измерений. Назначение таких сетей - быть основой различного рода съемок, необходимых для решения научных, народохозяйственных и оборонных задач. К основным сетям относится та часть геодезических сетей, которая имеет высокую точность линейных и угловых элементов и обеспечивает относительную погрешность взаимного положения пунктов сети ≤ 1:10000. В зависимости от точности угловых и линейных измерений, а также длинны сторон, основные сети подразделяются на классы и разряды. Высшие классы (1 и 2кл), распространенные на всю территорию России, составляют главную геодезическую основу страны. 3 и 4 классы являются сетями сгущения 1 и 2 класса. Построения основных геодезических сетей ведется методами триангуляции, полигонометрии и трилатерации. В последнее время (с 90 годов 20 века) для построения сетей используются методы спутниковых (GPS) определений.
Полигонометрия - это комбинация линейно-угловых измерений на местности, в виде отдельных ходов или сетей (полигонов), и предназначена для определения плоских прямоугольных координат геодезических пунктов в заданной системе счисления (СК-42, СК-63, СК-95 и т.д.). В большинстве случаев, пункты полигонометрии совмещают с пунктами нивелирной сети. Такие пункты кроме плановых координат имеют высотные отметки.
Основные характеристики полигонометрии 4 класса. Таблица 1.
Полигонометрические хода и сети 4 кл., 1 и 2 разрядов прокладываются в соответствии с требованиями, предъявляемыми к основным геодезическим сетям, которые вынесены в таблицу 1 и 2 Основные характеристики полигонометрии I и 2 разрядов Таблица 2
Угловые измерения
Визирные марки и оптические центриры.
Для получения большей точности измерения углов, в полигонометрии используют специальные приспособления – визирные марки и оптические центриры. Визирная марка представляет собой визирную цель, ось симметрии которой расположена строго по отвесной линии и проходит через вершину измеряемого угла. Центрирование марки осуществляется с помощью специального приспособления – оптического или лазерного центрира.
Визирные марки. Визирная марка состоит из двух частей: 1. Подставка (трегер) - одинакова по конструкции с подставкой теодолита; 2. Металлический щиток укрепленный на оси, окрашенный в два цвета.
Рисунок и цвета окраски у различных конструкций марок различны. Чаще всего визирная цель, изображенная на марке, представляет собой либо перевернутый вверх основанием треугольник, вершина угла которого совпадает с осью симметрии марки, либо группу треугольников, окрашенных в два цвета, вершины которых сходятся в одной точке и совпадают с осью симметрии марки.
Рис. 1 По специальному заказу, завод УОМЗ (Уральский оптико-механический завод) комплектует теодолиты специальным набором марок – КВЦ (комплект визирных целей). Марки (4 шт.) покрыты специальной световозвращающей (флуоресцентной) эмалью, повышающей яркость и контрастность фона визирной цели в несколько раз, по сравнению с обычными красками, что дает возможность производить измерение углов со сторонами до 5 км. Кроме этого, на оси симметрии имеется небольшое отверстие, которое освещается лампочкой подсветки, что позволяет производить измерения в ночных условиях. В набор КВЦ также входят 2 оптических центрира с уровнями. Сами марки снабжены круглым уровнем.
Поверки визирных марок. Перед началом полевых работ, марки поверяются на асимметрию. Если марка снабжена круглым уровнем, то поверяется и круглый уровень. 1. Ось круглого уровня должна быть параллельна оси вращения марки. Это условие поверяется как обычно (у нивелира или теодолита). 2. Ось симметрии визирной цели марки должна совпадать с осью симметрии визирного щитка марки. Ось симметрии визирного щитка марки должна совпадать с осью вращения марки. Поверку производят измерением с помощью теодолита трех угловых расстояний, два из которых n1 и n3 (рис. 2) пройдут по краям щитка марки, а третье n2 пересечет ось визирной цели.
Рис. 2 Теодолит устанавливают в 3 – 5 метрах от марки, приводят ось вращения в отвесное положение, после чего наводят зрительную трубу поочередно на левый край марки, на центр визирной цели, на правый край марки, произведя отсчеты n1, n2, n3. По полученным отсчетам вычисляют разности:
Асимметрия визирной цели а относительно оси симметрии щитка марки выражается в линейной мере и определяется формулой:
где
S - расстояние от теодолита до марки. Для проверки асимметрии выполняют как правило 2 – 3 приема. Величина асимметрии а не должна превышать 1 мм. При большем ее значении марка бракуется.
Оптический центрир. Оптический центрир служит для центрирования визирных марок над центром заложенных знаков. Оптический центрир представляет собой короткофокусную зрительную трубу, снабженную двумя цилиндрическими уровнями, вставляемую в подставку (трегер) теодолита. По конструкции напоминает оптический отвес теодолита. В последние годы все большее применение получают лазерные центриры. Отличие от оптических центриров состоит в отсутствии зрительной трубы. Ее заменяет твердотельный бытовой лазер – указка.
Измерения углов. При проведении полигонометрических работ используют два способа измерения углов: 1. способ отдельного угла - когда направлений всего два; 2. способ круговых приемов – направлений более двух. Для точных теодолитов – 3Т2КП и им равноточных (Theo 010 и т.д.), точность измерения углов и количество приемов (число повторных измерений одного и того же угла) регламентируется инструкцией (Таблица 4), и зависит от класса и разряда полигонометрии. Таблица 4
А) Измерение угла способом приемов. Этот способ измерения угла известен из предыдущего курса. В тахеометрических работах, при развитии съемочного обоснования теодолитными ходами, для измерения углов использовался способ полуприемов, в котором отсчет на начальное направление при круге право изменялся на некоторую величину. В способе приемов данный сдвиг не делают. Перед началом измерений углов, производят расчет изменения начальных установок в каждом приеме в соответствии с формулой 3:
где n - число приемов; i - цена полуделения лимба теодолита.
Делается это для того, чтобы задействовать все поле лимба горизонтального круга и, тем самым, ослабить влияние эксцентриситета лимба и рена оптического микрометра. Начальный отсчет в первом приеме устанавливают близким к 0º00'00". После выполнения измерений угла при двух кругах теодолита, к начальной установке каждого последующего приема добавляется расчетное число из (3).
В полигонометрии 4 класса углы измеряются 6 приемами. Начальные установки в приемах будут соответствовать данным приведенным в таблице 5: Таблица 5
Пример записи в журнал измерений и вычислений угла способом приемов приведен в таблице 6. Таблица 6
В таблице 6 в скобках (колонка «круг») указана последовательность наведения зрительной трубы Б) Измерение углов способом круговых приемов.
Данный способ применяется в тех случаях, когда требуется выполнить угловые измерения более двух направлений (рис. 3).
Рис. 3
Теодолит установлен в пункте 9. Требуется измерить левые по ходу углы между пунктами 8, В, 10.
Порядок измерения. 1. Производятся подготовительные работы для измерения углов. 2. При круге лево, наводят визирную ось зрительной трубы на визирную цель задней по ходу марки (8), которую принимают за начальное направление. 3. Устанавливают лимб и оптический микрометр на отсчет близкий к нулю. (Сначала вращением барабанчика оптического микрометра устанавливают отсчет по шкале последнего чуть больше нуля, затем вращением рукоятки фрикционного винта перестановки лимба тщательно совмещают изображения штрихов противоположных краев лимба 0 и 180º. Точное совмещение выполняют дополнительным установочным винтом, который полузакрыт защитным кожухом [для теодолита 3Т2КП]) 4. После этого барабанчиком микрометра штрихи разводят, после чего выполняют точное совмещение штрихов лимба и производят отсчет (первое совмещение), который записывают в журнал (см. таблица 6). Рекомендуется окончательное совмещение штрихов выполнять по ходу часовой стрелки – на ввинчивание, чтобы исключить механический люфт микрометра. 5. Барабаном микрометра разводят совмещенные штрихи, затем вновь выполняют точное совмещение (второе совмещение), производят отсчет и вновь записывают в журнал. Разность двух отсчетов не должна превышать 2". 6. Открепляют алидаду и направляют зрительную трубу в сторону ближайшей визирной цели по ходу часовой стрелки (В). Выполняют точное визирование, после чего снимают отсчеты по шкаловому микрометру при двух совмещениях. Отсчеты записывают в журнал. 7. Пункт 6 выполняют по отношению к третьей визирной цели (10). 8. Затем, наводят зрительную трубу на первую визирную цель (8) – производят “замыкание горизонта”. При двух совмещениях производят отсчеты и записывают их в журнал. На этом заканчиваются измерения в первом полуприеме. Повторное наведение на первую визирную цель (“замыкание горизонта”) производится для того, чтобы установить, сохранил ли лимб в процессе измерений неподвижное положение. Допуск на “замыкание горизонта” ≤ 8". После перевода зрительной трубы через зенит, при круге право КП, производят измерения второго полуприема в описанном выше порядке. При этом, визирные цели выбираются в обратном порядке – 8, 10, В, 8. Для последующих приемов выполняется переустановка начального отсчета в соответствии с (3).
Пример записи первого приема приведен в таблице 7. В каждом приеме выполняются следующие вычисления: 1. В графе 6 вычисляют средние значения из первого и второго совмещения по каждому направлению. 2. В графе 7 находят величину двойной коллимационной ошибки 2С. Постоянство величины 2С (колебания ее) допускается в пределах ±12 " и служит показателем качества измерений. Если 2С в приеме остается постоянной – качество измерений хорошее. 3. В графе 8 вычисляют среднее значение направления вычисленных в графе 6. 4. В графе 9 вычисляют приведенные к общему нулю направления. Для этого определяют незамыкания горизонта Δкл, Δкп, и Δср как разность конечного и начального направлений. 5. Величина Δср контролируется по следующему правилу Таблица 7 Пункт 9. Прием I. Наблюдатель: Cтепанов П.Г. Таблица 9
б) Если известны поперечные невязки по N вытянутым ходам, то среднюю квадратическую погрешность угла определяют по формуле 10 и 11
или
где u - поперечные невязки вытянутых ходов, вычисленные по углам, исправленным за угловую невязку; u' - поперечные невязки вытянутых ходов, вычисленные по неисправленным за угловую невязку углам;
Поперечная невязка u вычисляется по формуле:
где L -длина замыкающей хода
u' связанас u следующим соотношением:
В случае, если влияние погрешностей исходных данных на величины невязок ничтожны по сравнению с влиянием погрешностей полевых измерений, то формулы 8,10, 11 дадут близкие между собой значения mβ, которые действительно характеризуютточность угловых измерений. В случае, если влияние погрешностей исходных данных будет заметным, результаты вычислений по формулам 8, 10 и 11 дадут преувеличенные и не согласующиеся между собой результаты. Причем наибольшее отличие от истинных результатов даст формула 10, как наиболее чувствительная к погрешностям исходных данных, а наименьшее – формула 8, значение которой принимают за наиболее близкую к истинной величине. Значение и виды привязок. Общие положения. Привязка – это особый вид работ, позволяющий получить в процессе измерений дирекционный угол, расстояние или координаты определяемой точки по отношению к пунктам государственной геодезической сети (ГГС). Привязку к пунктам геодезической сети можно произвести различными способами в зависимости от расположения этих пунктов по отношению к определяемым точкам.
Наиболее простая привязка - это непосредственное примыкание хода к пунктам ГГС более высокого класса, с возможностью измерения примычных углов между пунктами ГГС и сторонами полигонометрического хода (в дальнейшем будем называть такой вид привязки - азимутальная).
Если имеется возможность непосредственной привязки хода к пунктам ГГС, но отсутствует возможность выполнить измерения примычных углов (утеряны ориентирные пункты, нет прямой видимости между пунктами ГГС), то такую привязку будем называть координатной. Если непосредственная привязка к пункту ГГС невозможна, то в этом случае используют особые способы привязок, позволяющие определить неизвестные параметры (координаты, расстояния, дирекционные углы, высоты). Такие измерения, выполняемые для определения отдельных координат точек местности с использованием пунктов геосети, называют засечками.
В привязочных работах очень часто приходится определять неприступные расстояния. Для этого используют стандартные построения и математические зависимости известные из тригонометрии – теоремы синусов и косинусов.
Для вычисления дирекционных углов и расстояний практически всегда используется обратная геодезическая задача, для определения приращений координат – прямая геодезическая задача.
Координатная привязка Возможны два варианта координатной привязки:
Вариант 1.
Предположим, что от пункта полигонометрии пп1 необходимо проложить ход (пп1,р1,р2 … и т.д.). Однако, в силу каких либо причин (построили дом, вырос лес и т.д.) видимость с пункта пп1 на пункт пп2 отсутствует. Выполнить непосредственную привязку (измерить примычный угол β1) не представляется возможным. В данном случае выполняется простейшая линейно-угловая засечка, в результате решения которой, аналитически вычисляется примычный угол β1 на точку хода. Для решения данной задачи, на пункты пп1 и пп2 устанавливаются штативы с визирными целями. На местности, выбирается точка хода р1, с которой имеется прямая видимость на пункт привязки пп1 и пункт ориентирования пп2. Точка р1 закрепляется на местности. Над точкой устанавливается прибор – теодолит или тахеометр – и измеряются:
Решение засечки сводится к решению треугольника р1пп1пп2, из которого находится угол β1. Для решения треугольника используется теорема синусов.
Для решения треугольника с использованием теоремы синусов необходимо определить расстояние L, между исходным пунктом пп1 и пунктом ориентирования пп2. Возможны два случая:
Вычислив L, используем теорему синусов для вычисления углов β1 и контрольного угла ε.
Из данного выражения находим угол β1:
Для контроля находят угол ε:
Контролем правильности вычислений служит известное из геометрии соотношение – сумма углов треугольника равна 180º или
где δ - предельная СКП измерения угла прибора, которым измерен угол φ.
Вариант 2. (координатная привязка) Имеются исходные пункты, но отсутствуют пункты ориентирования. Теория координатной привязки достаточно проста. Предположим, что через центр круга (рис. 5), радиусом R, проходит система координат XY. Радиус R1 в системе координат XY проведен под углом a и имеет приращения координат Dx1 и Dy1.
Рис 5 А радиус R1’ в той же системе координат XY проведен под углом a’ и имеет приращения координат Dx1’ и Dy1’. Несмотря на то, что сами приращения координат изменяются с изменением a, радиус данной окружности остается постоянным: R1= R1’ Используя теорему Пифагора можно записать
Для вычисления приращений координат радиусов R1 и R1’ используем прямую геодезическую задачу:
Dx1= Rcos(a); Dy1= Rsin(a); Dx1’ = R’cos(a’); Dy1’ = R’sin(a’);\ Для того, чтобы через радиус R’ вычислить приращения координат радиуса R, R’ необходимо довернуть на угол da = a - a¢ и тогда приращения координат будут одни и те же.
Dx1 = R’cos(a’ + da); Dy1 = R’sin(a’ + da); Алгоритм решения задачи. Предположим, что между двумя твердыми пунктами Т1 и Т2 проложили ход с координатной привязкой. (рис. 6) Необходимо вычислить координаты поворотных точек в системе координат ГГС.
Рис. 6
Исходя из изложенного, предположим, что пункт Т1 начало вектора R1, а пункт Т2 его конец. Задача решается в два приближения.
Первое приближение. Второе приближение Далее используется стандартный алгоритм вычисления рабочих координат. Отличие состоит в том, что в данном алгоритме отсутствует угловая невязка, которая скомпенсировалась доворотом хода – замыкающая хода совпадает с истинной замыкающей. Пример вычисления рабочих координат полигонометрического хода (координатная привязка). Рассмотрен предыдущий пример.Исходные дирекционные углы изъяты из вычислений Первое приближение
После того, как в первом приближении вычислили угол доворота и дирекционный угол замыкающей, выполняют второе приближение, в котором вычисляют окончательные координаты точек хода. Для этого первая измеренная линия хода принимает значение вычисленного дирекционного угла. Второе приближение
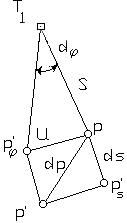
Оценка точности Для получения средней квадратической ошибки положения пункта Р воспользуемся рис. 8
рис. 8 Допустим, что под влиянием ошибок в длине линии где
тогда
или
Переходя к среднеквадратическим погрешностям перепишем данную формулу следующим образом:
где М Как видно из формулы, для определения погрешности положения пункта Р необходимо вычисление среднеквадратических погрешностей вычисленных элементов: линии Для проведения оценки точности необходимо иметь показатели точности измерения базисов ( Для получения
при этом учтем, что угол
Переходя к среднеквадратическим погрешностям и принимая
Средняя квадратическая погрешность среднего значения линии
Величинами
Тогда
Определим среднюю квадратическую погрешность дирекционного угла
где i = 1, 2. Угол
В свою очередь величина
Несколько упростим его, имея в виду, что отношение С учетом этого (17) можно записать
Дифференцируя ее, получим
откуда найдем
Можно считать, что отношение
Тогда Учитывая это соотношение в формуле (
или с учетом
Отсюда, переходя к среднеквадратическим погрешностям, будем иметь
Строгая формула среднеквадратической погрешности дирекционного угла примет следующий вид
Средняя квадратическая погрешность среднего значения дирекционного угла
где Предельное расхождение между значениями
Анализ формул показывает, что для обеспечения большей точности передачи координат с пункта Т1 на пункт Р необходимо: а) строить по возможности равносторонние вспомогательные треугольники АРТ1и BРT1, это обеспечит большую точность вычисления s;
б) выбирать положение пункта Р так, чтобы угол
Пример вычислений на снесение координат(см рис. 7). (В процессе привязки в обязательном порядке делается абрис привязки, т. е. в обязательно указывается расположение пунктов Т2 и Т3 относительно пункта Т1 и точки привязки Р [для правильного использования формулы
|



 ;
; (1).
(1). (2);
(2); - разность значений углов (1);
- разность значений углов (1);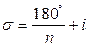 (3);
(3);

 .
.
 ;
;  .
. (10),
(10), (11),
(11),

 ( 12 )
( 12 )



 ;
; .
. .
. .
. .
.






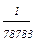
 и в дирекционном угле
и в дирекционном угле  пункт Р сместился со своего истинного положения на величину
пункт Р сместился со своего истинного положения на величину  и попал в точку Р’. Это смещение можно разложить на компоненты
и попал в точку Р’. Это смещение можно разложить на компоненты  ,
, ,
, (24).
(24).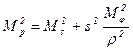 (25),
(25), и Мs — среднеквадратические погрешности
и Мs — среднеквадратические погрешности  и
и  .
.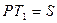 , дирекционного угла
, дирекционного угла  и положения пункта Р.
и положения пункта Р. — при измерении базиса светодальномером и углов -
— при измерении базиса светодальномером и углов -  ,
,  ,
,  ).
). возьмем функцию
возьмем функцию  , прологарифмируем ее, а затем продифференцируем полученное выражение и найдем
, прологарифмируем ее, а затем продифференцируем полученное выражение и найдем (26),
(26), определяется по формуле
определяется по формуле  , следовательно,
, следовательно, .
. (углы измерены равноточно), найдем
(углы измерены равноточно), найдем . (27)
. (27)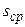 будет
будет (28).
(28). можно воспользоваться для подсчета предельного расхождения в значениях S, вычисленных из двух треугольников, так как
можно воспользоваться для подсчета предельного расхождения в значениях S, вычисленных из двух треугольников, так как ,
, .
. (29).
(29). . Дифференцируя формулы
. Дифференцируя формулы  , получим
, получим (30),
(30), вычисляется по формуле
вычисляется по формуле  , следовательно, дифференцирование ее дает
, следовательно, дифференцирование ее дает (31).
(31). определяется выражением
определяется выражением .
. , как правило, в практике работ, составляет приблизительно
, как правило, в практике работ, составляет приблизительно  .
. .
.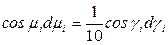 ,
, .
. .
.
 ), можно
), можно  , при оценке точности, в расчет не принимать, тогда
, при оценке точности, в расчет не принимать, тогда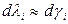 ,
,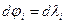
 .
. (32).
(32). (33).
(33).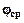 в случае определенияего по двум пунктам Т2 и Т2’(с учетом ф-ла 32) примет вид
в случае определенияего по двум пунктам Т2 и Т2’(с учетом ф-ла 32) примет вид (34)
(34) .
. (35).
(35). был близок к прямому.
был близок к прямому. ]. Если пункт Т2 или Т3 расположен справа от точки привязки и пункта Т1, то в формуле выбирается знак «+», в противном случае знак «-»)
]. Если пункт Т2 или Т3 расположен справа от точки привязки и пункта Т1, то в формуле выбирается знак «+», в противном случае знак «-»)


