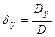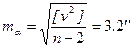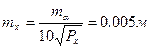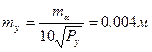Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
A. Вычисление приближенных дирекционных углов и расстоянийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
B. Вычисление свободных членов уравнений поправок
3. Вычисление коэффициентов параметрических уравнений поправок Для этого дирекционные углы направлений на пункт Р округляют до целых минут. Для того, чтобы не работать с большими числами при ручном вычислении, коэффициенты (а) и (b) делят на 10000, а при вычислении коэффициентов a и b расстояние S берется в километрах.
4. Вычисление коэффициентов нормальных уравнений
При вычислении коэффициентов нормальных уравнений поправок выполняется подсчет сумм коэффициентов as=aa+ab+al и bs=ab+bb+bl. Контролем правильности вычислений коэффициентов нормальных уравнений является равенство [as]=[aa]+[ab]+[al] и [bs]=[ab]+[bb]+[bl].
5. Решение нормальных уравнений
I. [aa]dx+[ab]dy+[al]=0 II. [ab]dx+[bb]dy+[bl]=0
Или в числовом выражении для нашего примера
3588.3dx + 469.6dy + 98.2 = 0 469.6dx + 7199.3dy +(-313.5)= 0
Данные уравнения решают способом детерминантов. Для этого необходимо найти определители системы уравнений, с учетом правил линейной алгебры и учетом расстановки знаков при вычислении миноров:
(-1)(n-1)*(вычисление определителя)
Где n – номер “вычеркнутого” столбца. Итак:
А. Основной определитель: D = [aa][bb] - [ab][ab] B. Определитель для столбца Х Dx = [ab][bl] - [bb][al] С. Определитель для столбца Y Dy = [ab][al] - [aa][bl] Вычислив определители, найдем поправки в приближенные координаты:
Сведем данные вычисления в таблицу:
С учетом того, что при вычислении коэффициентов (а) и (b) выполнено деление на 10000, а при вычислении коэффициентов а и b S взято в километрах, размерность вычисленных поправок – дециметры. Для перевода в метры, их необходимо домножить на 0.1 dx =-0.033 Px = D/[bb] 3557.7 dy = 0.046 Px = D/[aa] 7137.8
Перед тем, как вычислить окончательно уравненные координаты определяемого пункта, необходимо вычислить поправки в измеренные дирекционные углы и выполнить контроль вычисления поправок, что будет являться окончательным контролем правильности составления нормальных уравнений.
6. Вычисление поправок v и уравнивание дирекционных углов. Поправки вычисляют в соответствии с формулой
7. Контроль вычисления поправок. Контролем вычисления поправок служит уравнение [al]dx+[bl]dy+[ll]=[v2]
Убедившись в правильности составления и решения нормальных уравнений поправок можно приступить к окончательному вычислению уравненных координат определяемого пункта и выполнить оценку точности измерений.
8. Окончательно уравненные координаты пункта P
X уравн. = X’ + 0.1dx = 18144.581 Y уравн. = Y’ + 0.1dy = 17184.391
9. Оценка точности
Для определения среднеквадратических погрешностей вычисленных координат определяемого пункта необходимо вычислить веса:
Px = D/[bb] = 3557.7 Py = D/[aa] = 7137.8 Тогда
В вычислениях присутствует цифра 10. В нашем примере она появилась из вычисления коэффициентов (а) и (b).
10. Вычисление дирекционных углов и расстояний по уравненным координатам
Данные вычисления являются окончательным контролем всех вычислений.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 701; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

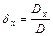 и
и