
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пункт, к которому производится привязка, недоступен ни для линейных, ни для угловых измерений (обычно это шпиль какого-либо здания или колокольни церкви).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Итак, необходимо определить координаты пункта Р (рис. 7), из которого видны пункты обоснования: близко расположенный пункт Т1 и пункт Т2, последний может быть расположен на значительном расстоянии от пункта Р. Более надежный контроль решения задачи будет обеспечен в том случае, если, кроме пункта Т2, будет виден еще пункт T3. Расстояние (Оптимальная длина базиса – получение равносторонних треугольников Из треугольников
рис. 7 где
i = 1, 2. Из полученных значений берут среднее. Для определения примычного угла В треугольнике РТ1Т2 дирекционный угол линии (T1T2) и ее длину Т1T2 = L1 находят из решения обратной геодезической задачи по формулам
Зная величину L1, из треугольника РТ1Т2 по теореме синусов находят
а затем — угол Примычный угол
Дирекционный угол
Выбор знака перед По полученным длине линии РТ1 и дирекционному углуее(T1Р), решая прямую геодезическую задачу, находят приращения координат,
а затем сами координаты
Заключительный контроль решения задачи состоит в вычислении дирекционного угла (РТ2) из обратной геодезической задачи
и вторичном получении угла
Если из пункта Р будет виден пункт Оценка точности Для получения средней квадратической ошибки положения пункта Р воспользуемся рис. 8
рис. 8 Допустим, что под влиянием ошибок в длине линии
где
тогда
или
Переходя к среднеквадратическим погрешностям перепишем данную формулу следующим образом:
где М Как видно из формулы, для определения погрешности положения пункта Р необходимо вычисление среднеквадратических погрешностей вычисленных элементов: линии Для проведения оценки точности необходимо иметь показатели точности измерения базисов ( Для получения
при этом учтем, что угол
Переходя к среднеквадратическим погрешностям и принимая
Средняя квадратическая погрешность среднего значения линии
Величинами
Тогда
Определим среднюю квадратическую погрешность дирекционного угла
где i = 1, 2. Угол
В свою очередь величина
Несколько упростим его, имея в виду, что отношение С учетом этого (17) можно записать
Дифференцируя ее, получим
откуда найдем
Можно считать, что отношение
Тогда Учитывая это соотношение в формуле (
или с учетом
Отсюда, переходя к среднеквадратическим погрешностям, будем иметь
Строгая формула среднеквадратической погрешности дирекционного угла примет следующий вид
Средняя квадратическая погрешность среднего значения дирекционного угла
где Предельное расхождение между значениями
Анализ формул показывает, что для обеспечения большей точности передачи координат с пункта Т1 на пункт Р необходимо: а) строить по возможности равносторонние вспомогательные треугольники АРТ1и BРT1, это обеспечит большую точность вычисления s;
б) выбирать положение пункта Р так, чтобы угол
Пример вычислений на снесение координат(см рис. 7). (В процессе привязки в обязательном порядке делается абрис привязки, т. е. в обязательно указывается расположение пунктов Т2 и Т3 относительно пункта Т1 и точки привязки Р [для правильного использования формулы
Решение. 1. Вычисление неприступного расстояния S (T1P) из треугольников I – AT1P и II - BT1P. Используется формула теоремы синусов.
2 Вычисления расстояний и дирекционных углов направлений T1T2 и T1T3. При вычислении используется обратная геодезическая задача.
3 Вычисление дирекционного угла линии S (T1P). Для этого, из треугольников Т1Т2P и Т1Т3P находим промежуточный угол μ1 и μ2. Данные углы необходимы для нахождения углов λ1 и λ2, с помощью которых находим искомый дирекционный угол линии S (T1P). А) Нахождение угла μ (i) – используется теорема синусов
Б) Нахождение угла λ1 и λ2 (используется свойство суммы углов треугольника = 180 ° ) и дирекционного угла φ линии S (T1P).
4. Вычисление координат P
5. Оценка точности измерений. А)Вычисление ms и Мs
Б)Вычисление Мфи и Мр
2. Пункт, к которому производится привязка, доступен для угловых, но не доступен для линейных измерений. Таким пунктом может быть, например, геодезический знак, построенный на крыше какого-либо дома, что часто имеет место в городах.
В этом случае величина угла
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 647; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.108.80 (0.013 с.) |

 можно определить как неприступное. Для этого на местности строят два треугольника
можно определить как неприступное. Для этого на местности строят два треугольника  и
и  . Стороны этих треугольников АР (b1) и РВ (b2) измеряют непосредственно; кроме этого, в каждом треугольнике измеряют по два угла
. Стороны этих треугольников АР (b1) и РВ (b2) измеряют непосредственно; кроме этого, в каждом треугольнике измеряют по два угла  ,
,  ,
,  и
и 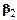 .
. по формуле
по формуле (13)
(13)
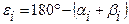 (14),
(14), на местности при точке Р измеряют угол
на местности при точке Р измеряют угол  . Этот угол дает возможность определить сначала из треугольника РТ1Т2 угол
. Этот угол дает возможность определить сначала из треугольника РТ1Т2 угол  а затем и угол
а затем и угол  ; (15)
; (15) (16);
(16); , (17)
, (17) получают из того же треугольника как дополнение до 180°:
получают из того же треугольника как дополнение до 180°: (18).
(18). направления Т1Р определяют как
направления Т1Р определяют как (19).
(19). (20),
(20), (21).
(21). (22)
(22) (23).
(23). , его необходимо использовать для вторичного получения значения координат пункта Р, для чего следует на пункте Р измерить угол
, его необходимо использовать для вторичного получения значения координат пункта Р, для чего следует на пункте Р измерить угол  , а далее повторить решение задачи, начиная с получения
, а далее повторить решение задачи, начиная с получения  и
и  по формулам (15) и (16) и т. д. до конца.
по формулам (15) и (16) и т. д. до конца.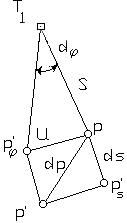
 и в дирекционном угле
и в дирекционном угле  пункт Р сместился со своего истинного положения на величину
пункт Р сместился со своего истинного положения на величину  и попал в точку Р’. Это смещение можно разложить на компоненты
и попал в точку Р’. Это смещение можно разложить на компоненты  ,
, ,
, (24).
(24).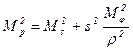 (25),
(25), и Мs — среднеквадратические погрешности
и Мs — среднеквадратические погрешности  и
и  .
.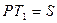 , дирекционного угла
, дирекционного угла  и положения пункта Р.
и положения пункта Р. — при измерении базиса светодальномером и углов -
— при измерении базиса светодальномером и углов -  ,
,  ,
,  ).
). возьмем функцию
возьмем функцию  , прологарифмируем ее, а затем продифференцируем полученное выражение и найдем
, прологарифмируем ее, а затем продифференцируем полученное выражение и найдем (26),
(26), определяется по формуле
определяется по формуле  , следовательно,
, следовательно, .
. (углы измерены равноточно), найдем
(углы измерены равноточно), найдем . (27)
. (27)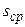 будет
будет (28).
(28). можно воспользоваться для подсчета предельного расхождения в значениях S, вычисленных из двух треугольников, так как
можно воспользоваться для подсчета предельного расхождения в значениях S, вычисленных из двух треугольников, так как ,
, .
. (29).
(29). . Дифференцируя формулы
. Дифференцируя формулы  , получим
, получим (30),
(30), вычисляется по формуле
вычисляется по формуле  , следовательно, дифференцирование ее дает
, следовательно, дифференцирование ее дает (31).
(31). определяется выражением
определяется выражением .
. , как правило, в практике работ, составляет приблизительно
, как правило, в практике работ, составляет приблизительно  .
. .
.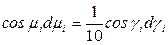 ,
, .
. .
.
 ), можно
), можно  , при оценке точности, в расчет не принимать, тогда
, при оценке точности, в расчет не принимать, тогда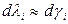 ,
,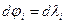
 .
. (32).
(32). (33).
(33).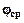 в случае определенияего по двум пунктам Т2 и Т2’(с учетом ф-ла 32) примет вид
в случае определенияего по двум пунктам Т2 и Т2’(с учетом ф-ла 32) примет вид (34)
(34) .
. (35).
(35). был близок к прямому.
был близок к прямому. ]. Если пункт Т2 или Т3 расположен справа от точки привязки и пункта Т1, то в формуле выбирается знак «+», в противном случае знак «-»)
]. Если пункт Т2 или Т3 расположен справа от точки привязки и пункта Т1, то в формуле выбирается знак «+», в противном случае знак «-») измеряется и задача сводится к вычислению неприступного расстояния Т1Р=S, которое определяется из решения двух треугольников АРТ1 и BРT1. Углы
измеряется и задача сводится к вычислению неприступного расстояния Т1Р=S, которое определяется из решения двух треугольников АРТ1 и BРT1. Углы  и
и  в этих треугольниках измеряются непосредственно.
в этих треугольниках измеряются непосредственно.


