
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приборы для измерения свойств жидкости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приборы для измерения свойств жидкости. Ареометр - прибор для измерений плотности жидкостей и твёрдых тел. Пьезометр (от греч. piézo — давлю, сжимаю и метр), устройство, служащее для измерения изменения объёма веществ под воздействием гидростатического давления Гидростатика (от гидро... и статика), раздел гидромеханики, в котором изучаются равновесие жидкости и воздействие покоящейся жидкости на погруженные в неё тела. Одна из основных задач Г.— изучение распределения давления в жидкости. Зная распределение давления, можно на основании законов Г. рассчитать силы, действующие со стороны покоящейся жидкости на погруженные в неё тела, например на подводную лодку, на стенки и дно сосуда, на стену плотины и т.д. В частности, можно вывести условия плавания тел на поверхности или внутри жидкости, а также выяснить, при каких условиях плавающие тела будут обладать устойчивостью, что особенно важно в кораблестроении. На законах Г., в частности на Паскаля законе, основано действие гидравлического пресса, гидравлического аккумулятора, жидкостного манометра, сифона и многих др. машин и приборов. Если покоящаяся тяжёлая жидкость имеет свободную поверхность, во всех точках которой внешнее давление равно р0, то давление жидкости на глубине h равно: p=p0+rgh, т. е. давление на глубине h равно внешнему давлению, сложенному с весом столба жидкости, высота которого равна h, а площадь основания равна единице (r — плотность жидкости, g — ускорение свободного падения). Свойства давления, выражаемые этой формулой, используются в гидростатических машинах (в гидравлическом прессе, гидравлическом аккумуляторе и др.). Один из основных законов Г. — Архимеда закон определяет величину подъёмной силы, действующей на тело, погруженное в жидкость или газ. Часто встречаются случаи, когда жидкость движется вместе с сосудом так, что по отношению к сосуду она покоится. На основе законов Г. можно определить форму поверхности жидкости в таком сосуде, например во вращающемся. Поскольку поверхность жидкости всегда устанавливается таким образом, чтобы сумма всех сил, действующих на частицы жидкости, кроме сил давления, была нормальна к поверхности, в цилиндрическом сосуде, равномерно вращающемся вокруг вертикальной оси, поверхность жидкости принимает форму параболоида вращения. Так же обстоит дело в океанах — поверхность воды не является в точности шаровой, а несколько сплюснута к полюсам. Этим же в какой-то степени объясняется сплюснутая к полюсам форма самого земного шара. Т. о., законы Г., позволяющие определить форму поверхности равномерно вращающейся жидкости, важны в космогонии.
Гидростатическое давление В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна. Рассмотрим резервуар с плоскими вертикальными стенками, наполненный жидкостью (рис.2.1, а). На дно резервуара действует сила P равная весу налитой жидкости G = γ V, т.е. P = G. Если эту силу P разделить на площадь дна Sabcd, то мы получим среднее гидростатическое давление, действующее на дно резервуара. Гидростатическое давление обладает свойствами: Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости. Свойство 2. Гидростатическое давление неизменно во всех направлениях. Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве. Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила - сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики. Жидкость, заключенная в неподвижный резервуар и находящаяся в равновесии под действием силы тяжести, пребывает в абсолютном покое относительно Земли Жидкость может находиться в равновесии и при действии помимо собственного веса других внешних сил, в том числе и сил инерции. Жидкое тело в таком случае будет находиться в относительном покое. Следует при этом иметь в виду, что жидкость, начавшая двигаться из состояния абсолютного покоя, приходит в состояние относительного покоя не сразу и переход из одного состояния в другое происходит под влиянием сил трения. В самом состоянии относительного покоя силы трения отсутствуют. В качестве примера рассмотрим равновесие жидкости в движущейся цистерне, вращающемся сосуде и движущемся по наклонной плоскости резервуаре Если цистерна движется прямолинейно и равноускоренно по горизонтальной поверхности, то жидкость находится в покое относительно этой цистерны. Датчик давления состоит (рис.1) из первичного преобразователя давления, в составе которого чувствительный элемент и приемник давления, схемы вторичной обработки сигнала, различных по конструкции корпусных деталей и устройства вывода. Основным отличием одних приборов от других является точность регистрации давления, которая зависит от принципа преобразования давления в электрический сигнал: тензометрический, пьезорезисторный, емкостной, индуктивный, резонансный, ионизационный. Основные понятия, используемые в кинематике жидкости Сутью вышеупомянутого поля скоростей являются векторные линии, которые часто называют линиями тока. Линия тока – такая кривая линия, для любой точки которой в выбранный момент времени вектор местной скорости направлен по касательной (о нормальной составляющей скорости речь не идет, поскольку она равна нулю).
Формула (1) является дифференциальным уравнением линии тока в момент времени t. Следовательно, задав различные ti по полученным i, где i = 1,2, 3, …, можно построить линию тока: ею будет огибающая ломаной линии, состоящей из i. Линии тока, как правило, не пересекаются в силу условия ≠ 0 или ≠ ∞. Но все же, если эти условия нарушаются, то линии тока пересекаются: точку пересечения называют особой (или критической). 1. Неустановившееся движение, которое так называется из-за того, что местные скорости в рассматриваемых точках выбранной области по времени изменяются. Такое движение полностью описывается системой уравнений. 2. Установившееся движение: поскольку при таком движении местные скорости не зависят от времени и постоянны: ux = ux(x,y,z) uy = uy(x,y,z) uz = uz(x,y,z) Линии тока и траектории частиц совпадают, а дифференциальное уравнение для линии тока имеет вид:
Совокупность всех линий тока, которые проходят через каждую точку контура потока, образует поверхность, которую называют трубкой тока. Внутри этой трубки движется заключенная в ней жидкость, которую называют струйкой. Струйка считается элементарной, если рассматриваемый контур бесконечно мал, и конечной, если контур имеет конечную площадку. Сечение струйки, которое нормально в каждой своей точке к линиям тока, называется живым сечением струйки. В зависимости от конечности или бесконечной малости, площадь струйки принято обозначать, соответственно, ω и dω. Некоторый объем жидкости, который проходит через живое сечение в единицу времени, называют расходом струйки Q. 3,1. Вихревое движение Особенности видов движения, рассматриваемых в гидродинамике. Можно выделить следующие виды движения. Неустановившееся, по поведению скорости, давления, температуры и т. д.; установившееся, по тем же параметрам; неравномерное, в зависимости от поведения тех же параметров в живом сечении с площадью; равномерное, по тем же признакам; напорное, когда движение происходит под давлением p > pатм, (например, в трубопроводах); безнапорное, когда движение жидкости происходит только под действием силы тяжести. Однако основными видами движения, несмотря на большое количество их разновидностей, являются вихревое и ламинарное движения. Движение, при котором частицы жидкости вращаются вокруг мгновенных осей, проходящих через их полюсы, называют вихревым движением. Это движение жидкой частицы характеризуется угловой скоростью, компонентами (составляющими), которой являются:
Вектор самой угловой скорости всегда перпендикулярен плоскости, в которой происходит вращение. Если определить модуль угловой скорости, то
Удвоив проекции на соответствующие координаты оси ωx, ωy, ωz, получим компоненты вектора вихря θ = 2ω. Совокупность векторов вихря называется векторным полем. По аналогии с полем скоростей и линией тока, существует и вихревая линия, которая характеризует векторное поле. Это такая линия, у которой для каждой точки вектор угловой скорости сонаправлен с касательной к этой линии. Линия описывается следующим дифференциальным уравнением:
в котором время t рассматривается как параметр. Вихревые линии во многом ведут себя так же, как и линии тока. Вихревое движение называют также турбулентным. 3.2. Ламинарное движение Это движение, называют также потенциальным (безвихревым) движением. При таком движении отсутствует вращение частиц вокруг мгновенных осей, которые проходят через полюсы жидких частиц. По этой причине: υx = 0; υy = 0; υz = 0. (1) ωx = ωy = ωz = 0. Выше отмечалось, что при движении жидкости происходит не только изменение положения частиц в пространстве, но и их деформация по линейным параметрам. Если рассмотренное выше вихревое движение является следствием изменения пространственного положения жидкой частицы, то ламинарное (потенциальное, или безвихревое) движение является следствием деформационных явлений линейных параметров, например, формы и объема. Вихревое движение определялось направлением вихревого вектора
где υ – угловая скорость, которая является характеристикой угловых деформаций. Деформацию этого движения характеризируют деформацией этих компонентов
Но, поскольку при ламинарном движении υx=υy= υz= 0, то:
Из этой формулы видно: поскольку существуют частные производные, связанные между собой в формуле (4), то эти частные производные принадлежат некоторой функции.
5. Гидродина́мика — раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа. Как и в других разделах физики сплошных сред, прежде всего осуществляется переход от реальной среды, состоящей из большого числа отдельных атомов или молекул, к абстрактной сплошной среде, для которой и записываются уравнения движения. Расход воды (в водотоке) — количество воды, протекающей через поперечное сечение водотока. Измеряется в расходных единицах (м³/с). В промышленности расход вода (жидкости) измеряется расходомерами. Средняя скорость потока - величина, полученная делением расхода воды, протекающей через сечение, нормальное к направлению течения потока, на площадь его сечения. Напо́р, в гидравлике и гидродинамике — давление жидкости, выражаемое высотой столба жидкости над выбранным уровнем отсчёта. Выражается в линейных единицах. Полный запас удельной энергии потока (полный напор) определяется уравнением Бернулли и включает в себя: высоту рассматриваемой точки над плоскостью отсчёта (гидростатический напор), давление жидкости, обусловленное скоростью потока (скоростной напор). Вдоль потока напор уменьшается. Разность напора в двух поперечных сечениях потока реальной жидкости называется потерянным напором. Расход потока Q - объем жидкости V, протекающей за единицу времени t через живое сечение ω.
Бернулли имеет следующий вид:
в широком смысле слова дроссель — это ограничитель, регулятор Одной из важнейших формул, применяемых для расчета потерь напора на трение в трубопроводе, является формула Дарси-Вейсбаха:
Δhfr = λ(l/d)(V2/2g), (1)
где λ – коэффициент гидравлического сопротивления; l/d – относительная длина трубопровода; V2/2g – скоростной напор.
Но λ – это вовсе не коэффициент, а самый настоящий критерий подобия. При ламинарном режиме течения это производный критерий подобия λ = 64/Re, а при турбулентном режиме течения – это функция не только от Re, но и от параметрического критерия подобия k/d, называемого относительной шероховатостью. Да и l/d – тоже параметрический критерий подобия, называемый относительной длиной трубопровода. Формула Никурадзе
Жидкость вытекает в воздушное пространство с давлением Р1. Пусть отверстие имеет форму, показанную на рис.5.2, а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или имеет форму, показанную на рис.5.2, б, т.е. выполнено в толстой стенке, но с заострением входной кромки с внешней стороны. Струя, отрываясь от кромки отверстия, несколько сжимается (рис.5.2, а). Такое сжатие обусловлено движением жидкости от различных направлений, в том числе и от радиального движения по стенке, к осевому движению в струе. 5.4. Истечение через насадки при постоянном напоре Внешним цилиндрическим насадком называется короткая трубка длиной, равной нескольким диаметрам без закругления входной кромки. На практике такой насадок часто получается в тех случаях, когда выполняют сверление в толстой стенке и не обрабатывают входную кромку. Истечение через такой насадок в газовую среду может происходить в двух режимах.
Первый режим - безотрывный режим. При истечении струя, после входа в насадок сжимается примерно так же, как и при истечении через отверстие в тонкой стенке. Затем струя постепенно расширяется до размеров отверстия из насадка выходит полным сечением При расчетах напорных трубопроводов основной задачей является либо определение пропускной способности (расхода), либо потери напора на том или ином участке, равно как и на всей длине, либо диаметра трубопровода на заданных расходе и потерях напора. В практике трубопроводы делятся на короткие и длинные. К первым относятся все трубопроводы, в которых местные потери напора превышают 5…10% потерь напора по длине. При расчетах таких трубопроводов обязательно учитывают потери напора в местных сопротивлениях. К ним относят, к примеру, маслопроводы объемных передач. Ко вторым относятся трубопроводы, в которых местные потери меньше 5…10% потерь напора по длине. Их расчет ведется без учета местных потерь. К таким трубопроводам относятся, например, магистральные водоводы, нефтепроводы. Учитывая гидравлическую схему работы длинных трубопроводов, их можно разделить также на простые и сложные. Простыми называются последовательно соединенные трубопроводы одного или различных сечений, не имеющих никаких ответвлений. К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями и т.д. К сложным относятся и так называемые кольцевые трубопроводы. 8. Уравне́ния Навье́ — Сто́кса — система дифференциальных уравнений в частных производных, описывающая движение вязкой ньютоновской жидкости. Уравнения Навье — Стокса являются одними из важнейших в гидродинамике и применяются в математическом моделировании многих природных явлений и технических задач. Названы по имени французского физика Луи Навье и британского математика Джорджа Стокса. Система состоит из двух уравнений: -уравнения движения, -уравнения неразрывности. В векторном виде для несжимаемой жидкости они записываются следующим образом:
Где
Иногда в систему уравнений Навье — Стокса дополнительно включают уравнение теплопроводности и уравнение состояния. При учёте сжимаемости уравнение Навье — Стокса принимает следующий вид:
где μ — коэффициент динамической вязкости, ζ — «вторая вязкость». Применение Будучи дополненным уравнениями переноса тепла и переноса массы, а также соответствующих массовых сил, система уравнений Навье — Стокса может описывать конвекцию, термодиффузию в жидкостях, поведение многокомпонентных смесей различных жидкостей и т. п. Если же в уравнение в качестве массовой силы ввести силу Лоренца, и дополнить систему уравнениями Максвелла для поля в сплошной среде, то модель позволяет описывать явления электро- и магнитогидродинамики. В частности, такие модели успешно применяются при моделировании поведения плазмы, межзвёздного газа. Одним из применений системы уравнений Навье — Стокса является описание течений в мантии Земли («проблема динамо»). Также вариации уравнения Навье — Стокса используются для описания движения воздушных масс атмосферы, в частности, при формировании прогноза погоды. Для описания реальных течений в различных технических устройствах приемлемую точность численного решения можно получить только при такой расчётной сетке, ячейки которой меньше самого мелкого вихря. Это требует очень больших затрат расчётного времени на современных компьютерах. Поэтому были созданы различные модели турбулентности, упрощающие расчёт реальных потоков.
Уравнение Эйлера — одно из основных уравнений гидродинамики идеальной жидкости. Названо в честь Л.Эйлера, получившего это уравнение в 1755 году. По своей сути является уравнением движения жидкости. Классическое уравнение Эйлера Рассмотрим движение идеальной жидкости. Выделим внутри неё некоторый объём V. Согласно второму закону Ньютона, ускорение центра масс этого объёма пропорционально полной силе, действующей на него. В случае идеальной жидкости эта сила сводится к давлению окружающей объём жидкости и, возможно, воздействию внешних силовых полей. Предположим, что это поле представляет собой силы инерции или гравитации, так что эта сила пропорциональна напряжённости поля и массе элемента объёма. Тогда
где S — поверхность выделенного объёма, g — напряжённость поля. Переходя, согласно формуле Гаусса — Остроградского, от поверхностного интеграла к объёмному и учитывая, что
В силу произвольности объёма V подынтегральные функции должны быть равны в любой точке:
Выражая конвективную производную через частные производные:
получаем уравнение Эйлера для движения идеальной жидкости в поле тяжести:
где
Частные случаи Несжимаемая жидкость Пусть ρ = const. Используя известную формулу,
перепишем соотношение в форме
Беря ротор и учитывая, что,
а частные производные коммутируют, получаем что
Адиабатическое течение В случае, если происходит адиабатическое движение жидкости, то уравнение Эйлера можно переписать с использованием тепловой функции в силу того, что при адиабатическом процессе энтропия s постоянна. Следовательно:
7. Гидравлический удар (гидроудар) — скачок давления в какой-либо системе, заполненной жидкостью, вызванный крайне быстрым изменением скорости потока этой жидкости за очень малый промежуток времени. Гидравлический удар способен вызывать образование продольных трещин в трубах, что может привести к их расколу, или повреждать другие элементы трубопровода. Общие сведения Явление гидравлического удара открыл в 1869 г. Н. Е. Жуковский. Увеличение давления при гидравлическом ударе определяется в соответствии с его теорией по формуле:
где Dp — увеличение давления в Н/м², ρ — плотность жидкости в кг/м³, v0 и v1 — средние скорости в трубопроводе до и после закрытия задвижки (срабатывания клапана) в м/с, с — скорость распространения ударной волны вдоль трубопровода. Жуковский доказал, что скорость распространения ударной волны c находится в прямо пропорциональной зависимости от сжимаемости жидкости, величины деформации стенок трубопровода, определяемой модулем упругости материала E, из которого он выполнен, а также от диаметра трубопровода. Следовательно, гидравлический удар не может возникнуть в трубопроводе, содержащем газ, так как газ легко сжимаем. Зависимость между скоростью ударной волны c, её длиной и временем распространения (L и τ соответственно) выражается следующей формулой:
Виды гидравлических ударов В зависимости от времени распространения ударной волны τ и времени перекрытия задвижки (заслонки, клапана, иного местного сопротивления) t, в результате которого возник гидроудар, можно выделить 2 вида ударов: -Полный (прямой) гидравлический удар, если t < τ -Неполный (непрямой) гидравлический удар, если t > τ При полном гидроударе фронт возникшей ударной волны движется в направлении, обратном первоначальному направлению движения жидкости в трубопроводе. Его дальнейшее направление движения зависит от элементов трубопровода, расположенных до закрытой задвижки. Возможно и повторное неоднократное прохождения фронта волны в прямом и обратном направлениях. При неполном гидроударе фронт ударной волны не только меняет направление своего движения на противоположное, но и частично проходит далее сквозь не до конца закрытую задвижку. Гидроударом часто называют следствие заполнения надпоршневого пространства в моторе водой,что приводит к внезапной остановке и поломке мотора из-за того, что жидкость практически несжимаема. Примеры Наиболее простым примером возникновения гидравлического удара является трубопровод с постоянным напором и установившимся движением жидкости, в котором была резко перекрыта задвижка или закрыт клапан. В скважинных системах водоснабжения гидроудар, как правило, возникает, когда ближайший к насосу обратный клапан расположен выше статического уровня воды более, чем на 9 метров, или ближайший к насосу обратный клапан имеет утечку, в то время как расположенный выше следующий обратный клапан держит давление. В обоих случаях в стояке возникает частичное разрежение. При следующем пуске насоса вода, протекающая с очень большой скоростью, заполняет вакуум и соударяется в трубопроводе с закрытым обратным клапаном и столбом жидкости над ним, вызывая скачок давления и гидравлический удар. Такой гидравлический удар способен вызвать образование трещин в трубах, разрушить трубные соединения и повредить насос и/или электродвигатель. Гидротаранный насос Механическое устройство для подъема воды на значительную (до нескольких десятков метров) высоту. Не требует для работы каких-либо внешних движителей, благодаря чему может быть весьма полезено в местности, где нет электроснабжения либо в местности малообжитой и редкопосещаемой. Энергию для работы насос получает из потока воды, перетекающего под действием силы тяжести из т.н. "питающего" резервуара (например, из запруды на реке) по "питающей" трубе в какой-либо нижерасположенный сток (например, в ту же реку ниже по течению). Пропуская через себя бОльшую часть воды с небольшой высоты h (разница высот между стоком и уровнем воды в питающем резервуаре) насос поднимает меньшую часть воды на бОльшую высоту H (разница высот между верхней точкой отводящей трубы и уровнем воды в питающем резервуаре). Термины не являются устоявшимися. Напрмер, питающая труба нередко именуется "напорной" и т.п. Устройство. Гидротаранный насос в простейшем случае состоит из а) питающей трубы б) отбойного клапана в) возвратного клапана г) воздушного колпака д) отводящей трубы
Работа. Начальное состояние: отбойный клапан Б открыт и утерживается в таком положении пружиной или грузом или т.п. Сила этой пружины превышает силу давления статического столба воды в питающей трубе на закрытый отбойный клапан. Возвратный клапан В закрыт. Воздушный колпак заполнен воздухом. По питающей трубе А поступает вода, разгоняясь до некой скорости, при которой отбойный клапан Б, увлекаемый потоком воды, преодолевает усилие своей пружины и закрывается, перекрыв сток. Инерция резко остановленой в питающей трубе воды создает гидроудар -- резкий скачок давления, величина которого определяется длиной питающей трубы и скоростью потока. Давление гидроудара преодолевает давление столба воды в отводящей трубе Д, возвратный клапан В открывается и часть воды из питающей трубы А проходит через него и поступает в отводящую трубу но, главным образом, в воздушный колпак Г, поскольку инерция массы воды в отводящей трубе Д препятствует такому быстрому, испульсному поступлению. Вода в питающей трубе остановлена, давление падает и приходит к статической величине, возвратный клапан закрывается, отбойный клапан открывается. Вода в питающей трубе начинает двигаться, постепенно ускоряясь, а в это время под давлением воздуха, поджатого в воздушном колпаке, поступившая в него порция воды продавливается в питающую трубу. Таким образом система возвращается в исходное состояние и начинает новый цикл работы. Существуют различные модификаци этой схемы, призванные улучшить производительность насоса. 6. Насо́с — проточная гидравлическая машина, служащая для перемещения и создания напора жидкостей всех видов, механической смеси жидкости с твердыми и коллоидными веществами или сжиженных газов. Следует заметить, что машины для перекачки и создания напора газов (газообразных жидкостей) выделены в отдельные группы и получили название вентиляторов и компрессоров. По принципу действия и конструкции насосы подразделяются на: -импеллерные (ламельные) насосы -пластинчатые (шиберные) самовсасывающие насосы -центробежно-шнековые (дисковые) насосы -винтовые (шнековые) -поршневые -центробежные -осевые -вихревые -роторные -струйные -диафрагменные -перистальтические -мембранные -абсорбционные -тараны -магниторазрядные. Объемные насосы Импеллерные насосы — обеспечивают ламинарный поток перекачиваемого продукта на выходе из насоса, и могут использоваться в качестве дозаторов Пластинчатые насосы — обеспечивают равномерное и спокойное всасывание перекачиваемого продукта на выходе из насоса, могут использоваться для дозирования. Могут быть как регулируемыми, так и нерегулируемыми. В пластинчатых регулируемых насосах изменение подачи осуществляется за счёт изменения объёма рабочей камеры благодаря смещению эксцентриситета ротора и статора. В качестве регулирующего устройства применяются гидравлические и механические регуляторы. Винтовые насосы — обеспечивают ровный поток перекачиваемого продукта на выходе из насоса, могут использоваться для дозирования Поршневые насосы — могут создавать весьма высокое давление, плохо работают с абразивными жидкостями, могут использоваться для дозирования Перистальтические насосы — создают невысокое давление, химически инертны, могут использоваться для дозирования Мембранные насосы — создают невысокое давление, химически инертны, могут использоваться для дозирования Вакуумный насос — насос, осуществляющий откачку за счёт периодического изменения объёма рабочей камеры Импеллерные (ламельные) насосы — не требуют предварительного залива продукта во всасывающий патрубок, способен создать разрежение и всосать перекачиваемый продукт. Поток перекачиваемого продукта ламинарный, спокойный, способен перекачивать например жидкость с кусочками фруктов не подвергая из механическому воздействию. Могут быть изготовлены в пищевом, маслобензостойком и кислотощёлочестойком исполнении Пластинчатые (шиберные) насосы — применяются для перекачки густых и труднотекучих продуктов, типа патоки, сгущенного молока, смолы. При исполнении с рубашкой обогрева используются для перекачки застывающих продуктов, типа шоколадных глазурей Динамические насосы Динамические насосы подразделяются на: Лопастные насосы, рабочим органом у которых служит лопастное колесо или мелкозаходный шнек. В них входят: Центробежные, у которых преобразование механической энергии привода в потенциальную энергию потока происходит вследствие центробежных сил, возникающих при взаимодействии лопаток рабочего колеса с жидкостью. Центробежные насосы подразделяют на: Центробежно-шнековый насос — вид центробежного насоса с подводом жидкости к рабочему органу выполненному в виде мелкозаходного шнека большого диаметра (дисков), расположенному по цетру, с выбросом по касательной вверх или бок от корпуса. Консольный насос — вид центробежного насоса с односторонним подводом жидкости к рабочему колесу, расположенному на конце вала, удаленном от привода. Осевые (пропеллерные) насосы, рабочим органом которых служит лопастное колесо пропеллерного типа. Жидкость в этих насосах перемещаются вдоль оси вращения колеса. Быстроходные насосы с высоким коэффициентом быстроходности, характеризуются большими значениями подач, но низких значениях напора. Полуосевые (диагональные, турбинные) насосы, рабочим органом которых служит полуосевое (диагональное, турбинное) лопастное колесо. Радиальные насосы, рабочими органами которых служат радиальные рабочие колеса. Тихоходные одноступенчатые и многоступенчатые насосы с высокими значениями напора при низких значениях подач. Центробежно-шнековые (дисковые) — способны перекачивать карамелизующиеся и склеивающиеся массы, типа клея Вихревые насосы — отдельный тип лопастных насосов, в которых преобразование механической энергии в потенциальную энергию потока (напор) происходит за счет вихреобразования в рабочем канале насоса. Струйные насосы, в которых перемещение жидкости осуществляется за счет энергии потока вспомогательной жидкости, пара или газа (нет подвижных частей, но низкий КПД). Тараны (гидротараны), использующие явление гидравлического удара для нагнетания жидкости (минимум подвижных частей, почти нет трущихся поверхностей, простота конструкции, способность развивать высокое давление на выходе, низкие КПД и производительность). Вихревые насосы Вихревые насосы — динамические насосы, жидкость в которых перемещается по периферии рабочего колеса в тангенциальном направлении. Преобразование механической энергии привода в потенциальную энергию потока (напор) происходит за счет множественных вихрей, возбуждаемых лопастным колесом в рабочем канале насоса. КПД идеального вихревого насоса не превышает 45 %. КПД реальных насосов обычно не превышает 30 %. Применение вихревого насосы оправдано при значении коэффициента быстроходности[неизвестный термин] ns < 40. Вихревые насосы в многоступенчатом исполнении значительно раширяют диапазон рабочих давлений при малых подачах, снижая коэффициент быстроходности до значений, характерных для насосов объемного типа. Вихревые насосы сочетают преимущества насосов объемного типа (высокие давления при малых подачах) и динамических насосов (линейная зависимость напора насоса от подачи, равномерность потока).
Вихревые насосы используются для перекачки чистых и маловязких жидкостей, сжиженных газов, в качестве дренажных насосов для перекачки горячего конденсата. Вихревые насосы обладают низкими кавитационными качествами. Кавитационный коэффициент быстроходности вихревых насосов C = 100..110. Физический смысл Число Рейнольдса есть отношение сил инерции, действующих в потоке, к силам вязкости. Также число Рейнольдса можно рассматривать как отношение кинетической энергии жидкости к потерям энергии на характерной длине. Приборы для измерения свойств жидкости. Ареометр - прибор для измерений плотности жидкостей и твёрдых тел. Пьезометр (от греч. piézo — давлю, сжимаю и метр), устройство, служащее для измерения изменения объёма веществ под воздействием гидростатического давления Гидростатика (от гидро... и статика), раздел гидромеханики, в котором изучаются равновесие жидкости и воздействие покоящейся жидкости на погруженные в неё тела. Одна из основных задач Г.— изучение распределения давления в жидкости. Зная распределение давления, можно на основании законов Г. рассчитать силы, действующие со стороны покоящейся жидкости на погруженные в неё тела, например на подводную лодку, на стенки и дно сосуда, на стену плотины и т.д. В частности, можно вывести условия плавания тел на поверхности или внутри жидкости, а также выяснить, при каких условиях плавающие тела будут обладать устойчивостью, что особенно важно в кораблестроении. На законах Г., в частности на Паскаля законе, основано действие гидравлического пресса, гидравлического аккумулятора, жидкостного манометра, сифона и многих др. машин и приборов. Если покоящаяся тяжёлая жидкость имеет свободную поверхность, во всех
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.46 (0.012 с.) |

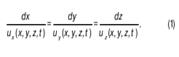

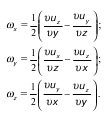
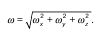


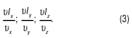





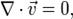
 — оператор Гамильтона, Δ — оператор Лапласа, t — время, ν — коэффициент кинематической вязкости, ρ — плотность, p — давление,
— оператор Гамильтона, Δ — оператор Лапласа, t — время, ν — коэффициент кинематической вязкости, ρ — плотность, p — давление,  — векторное поле скоростей,
— векторное поле скоростей,  — векторное поле массовых сил. Неизвестные p и являются функциями времени t и координаты
— векторное поле массовых сил. Неизвестные p и являются функциями времени t и координаты 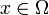 , где
, где  , n = 2,3 — плоская или трехмерная область, в которой движется жидкость. Обычно в систему уравнений Навье-Стокса добавляют краевые и начальные условия, например:
, n = 2,3 — плоская или трехмерная область, в которой движется жидкость. Обычно в систему уравнений Навье-Стокса добавляют краевые и начальные условия, например:
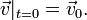


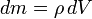 , где ρ — плотность жидкости в данной точке, получим:
, где ρ — плотность жидкости в данной точке, получим:



 — плотность жидкости,
— плотность жидкости,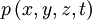 — давление в жидкости,
— давление в жидкости,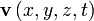 — вектор скорости жидкости,
— вектор скорости жидкости,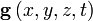 — вектор напряжённости силового поля,
— вектор напряжённости силового поля, — оператор набла для трёхмерного пространства.
— оператор набла для трёхмерного пространства.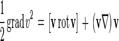
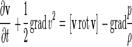
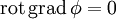
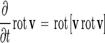
 следующим образом:
следующим образом: 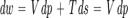
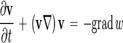
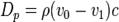 ,
,



