Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гидростатическое давление и его свойстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гидростатика - это раздел гидравлики, в котором рассматривают жидкости, находящиеся в состоянии покоя, то есть выполняется условие равновесия жидкости. Равновесие - это состояние покоя жидкости по отношению к некоторой системе координат, то есть скорости всех её частиц в любой момент времени равны нулю в той системе координат, в которой они рассматриваются. Для равновесия системы необходимо, чтобы сумма сил, приложенных к каждой частице жидкости массой ∆m, была равна нулю, то есть равна нулю сумма всех внешних сил, приложенных к данному объёму жидкости. Для выбранной системы координат сумма проекций сил на координатные оси равна нулю:
Внешние силы, действующие на данный объём жидкости, вызывают в этом объёме нормальные напряжения сжатия, так как жидкость не воспринимает растягивающие усилия. Так как жидкость находится в равновесии, то касательные напряжения τ, действующие только в движущейся жидкости (неньютоновские жидкости рассматривать не будем), не существуют. Основной задачей гидростатики является определение нормальных напряжений сжатия в жидкости.
Рис. 2.1. Схема к определению нормального напряжения сжатия
Рассмотрим некоторый объём жидкости, находящийся в равновесии (рис. 2.1), причём на этот объём действует какая-то внешняя сила (например, сила тяжести), вызывающая нормальные напряжения сжатия, распределённые по всему объёму жидкости. Для определения этих напряжений применим способ сечения. Способ сечения широко применяют в гидравлике в том случае, если необходимо исследовать напряжённое состояние внутри жидкости. Этот способ допускает рассечение или «вырезание» с помощью нескольких сечений некоторого объёма жидкости в виде любой правильной или произвольной фигуры. Дело в том, что напряжённое состояние внутри жидкости - это действующие между мельчайшими частицами жидкости во всех точках и направлениях внутренние силы. Отбрасывая от «вырезанного» объёма жидкости окружающую жидкость, необходимо заменить действие внутренних сил отброшенной жидкости внешней силой, определение которой и является одной из основных задач гидравлики. Рассечём некоторый объём жидкости произвольной плоскостью на две части, содержащие соответственно массы m 1 и m 2, и отбросим одну из них (например, верхнюю). Чтобы сохранить равновесие оставшейся массы m 2, необходимо приложить к ней силу, эквивалентную действию отброшенной массы m 1, причём эта сила будет равномерно распределена по площади сечения S. Сечение S можно представить состоящим из n -го количества элементарных площадок ∆ S, к каждой из которых приложена эквивалентная отброшенной массе m 1 сила ∆ Р, действующая по нормали к площадке.
Согласно (1.2), плотность распределения давления по площадке ∆ S равно пределу, к которому стремится отношение силы давления ∆ Р к площади ∆ S при уменьшении ∆ S до нуля, т. е. при стягивании её к размерам точки А:
Гидростатическое давление - это предел отношения силы гидростатического давления к площадке, на которую эта сила действует, при стремлении (стягивании) этой площадки к размерам точки. Силой гидростатического давления называют результирующую силу Р, действующую на сечение площадью S:
где Свойства гидростатического давления: 1. Гидростатическое давление направлено по нормали к площадке действия и является сжимающим. Это свойствоследует из условия равновесия жидкости; 2. Величина давления в данной точке не зависит от ориентации в пространстве площадки действия. Давление р в точке А (рис. 2.2) будет неизменным независимо от расположения в пространстве площадки, на которую действует давление жидкости;
Рис. 2.2. Схема к определению свойств гидростатического давления 3. Гидростатическое давление в данной точке зависит от её расположения в пространстве, то есть от координат в выбранной системе отсчёта, и от плотности жидкости: р = f (х, у, z, ρ). Зависимость гидростатического давления в некоторой точке жидкости от её координат (x, y, z) и плотности ρ определяется основным уравнением гидростатики.
|
|||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 577; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.19.115 (0.009 с.) |

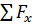 = 0;
= 0; 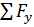 = 0;
= 0; 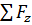 = 0.
= 0.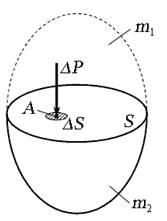
 . (2.1)
. (2.1) ,
, ,
,  .
.