
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Жидкости и их физические свойстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте О. В. Ворожцов
ГИДРАВЛИКА С ПРИМЕРАМИ РЕШЕНИЯ ЗАДАЧ Учебное пособие Рекомендовано к изданию Научно - методическим советом Псковского государственного университета
Псков Издательство ПсковГУ
УДК 556.556 ББК 30.123 В 751
Рекомендовано к изданию Научно - методическим советом Псковского государственного университета
Рецензент: Зав. кафедрой Менеджмент организации и управление инновациями, к. т. н. А. В. Стрикунов.
Ворожцов О. В. В 751 Гидравлика с примерами решения задач: Учебное пособие. - Псков: Издательство ПсковГУ, 2014. - 144 стр.
Учебное пособие по дисциплине «Гидравлика и гидропневмопривод» предназначено для студентов всех форм обучения технических специальностей. В пособии изложены основы физических свойств жидкости и газа, гидростатики и гидродинамики. Рассмотрены вопросы гидравлических сопротивлений, истечение жидкости через отверстия и насадки, гидродинамического воздействия жидкости на твёрдую преграду. Значительное внимание уделено практическому применению законов гидравлики. Представлены примеры решения задач.
УДК 556.556 ББК 30.123
© Ворожцов О. В. © Псковский государственный университет, 2014 Содержание
Введение Гидравлика - это наука, изучающая законы равновесия и движения жидкостей, а также законы взаимодействия жидкостей с окружающими их граничными поверхностями и с твердыми или упругими телами, погруженными (частично или полностью) в жидкость. Название «гидравлика» произошло от греческих слов «хюдор» - вода и «аулос» - труба, желоб. В настоящее время почти во всех областях техники применяют различные гидравлические устройства, основанные на использовании гидравлических законов. Основные области применения гидравлики – гидротехника, мелиорация и водное хозяйство, гидроэнергетика, водоснабжение и канализация, водный транспорт, машиностроение, авиация и т. д. Гидравлика делится на две части: гидростатику и гидродинамику. Гидростатика рассматривает законы равновесия жидкостей, находящихся в состоянии покоя. Гидродинамика изучает законы движения жидкостей и их взаимодействие с покоящимися или движущимися телами. Данное учебное пособие предназначено для студентов технических направлений подготовки. Большое внимание уделено решению задач, основанных на практическом применении законов гидравлики. Пособие может быть полезно студентам заочной формы обучения, доля самостоятельной работы которых особенно велика. Знание и эффективное применение законов гидравлики необходимо для решения практических задач, встречающихся в инженерной практике. Тем более, что гидросистемы различного назначения находят все бόльшее применение. Для лучшего понимания законов гидравлики и предназначено это пособие.
Жидкости и их физические свойства Жидкость. Основные понятия Жидкость - это физическое тело, обладающее текучестью. С точки зрения гидравлики как науки различают жидкость капельную (несжимаемую) и газообразную (сжимаемую). Капельная жидкость представляет собой жидкость в обычном, общепринятом понимании этого слова (вода, нефть, керосин, и т. д.). Капельную жидкость считают практически несжимаемой. Газообразная жидкость представляет собой газ (пропан, азот) или смесь газов (воздух). Газы в отличие от жидкостей заполняют всё предоставленное им пространство без образования свободной поверхности и легко изменяют свой объём в зависимости от изменения температуры и давления. Не смотря на существенные различия между жидкостями и газами, законы гидравлики применимы и к газам в случае их движения с дозвуковой скоростью. Поскольку жидкость обладает свойством текучести, она не может воспринимать растягивающие усилия. Однако при создании определенных условий вода может выдержать растягивающие усилия до 28∙106 Н/м2 (например, при попытке «растянуть» жидкость в закрытом гидроцилиндре, то есть при создании особых условий). Будем считать, что жидкость в обычных условиях испытывает только сжимающие усилия.
Воздух и его параметры Воздух используют в качестве рабочего тела в пневмосистемах, где он подвергается очистке от загрязнений и сжатию для создания рабочего давления. К загрязнениям относят загрязнения атмосферного воздуха, представляющие собой атмосферную пыль и некоторое количество водяного пара, и загрязнения, возникающие при сжатии. Сжатие воздуха сопровождается двумя видами загрязнений - водой (в жидком виде) и маслом. Загрязнение воздуха маслом существенно зависит от конструкции, качества и состояния компрессора. Смесь сухого воздуха и водяного пара называется влажным воздухом. Воздух, содержащий максимальное количество водяного пара, называется насыщенным. Предельное содержание влаги в воздухе отображено на графике (рис. 1.4).
Рис. 1.4. Предельное содержание влаги в воздухе в зависимости от температуры
Степень насыщенности воздуха влагой характеризует относительная влажность воздуха φ:
где dа - действительная влажность воздуха при некоторой температуре; d н - влажность насыщенного воздуха при той же температуре. Если действительное содержание влаги dа в воздухе остаётся неизменным, а температура воздуха снижается, то, согласно графику, представленному на рис. 1.4, уменьшается влажность насыщенного воздуха d н, и относительная влажность φ возрастает. Когда φ достигает уровня 100 %, воздух становится насыщенным. Температура, при которой это происходит, называется точкой росы. Дальнейшее снижение температуры сопровождается образованием конденсата. Зависимость точки росы от температуры и давления представлена на рис. 1.5.
Рис. 1.5. Зависимость точки росы воздуха от температуры и давления
Максимальное содержание влаги в воздухе для широкого диапазона температур и давлений приведены на рис. 1.6.
Рис. 1.6. Максимальное содержание водяного пара в 1 кг воздуха в зависимости от температуры и давления При сжатии воздуха и дальнейшем его охлаждении в ресивере происходит выпадение конденсата. Количество выпадающего конденсата при расчётах пневмосистем определяют следующим образом: - определяют исходные данные, к которым относят производительность компрессора, степень сжатия воздуха, температуру и действительную влажность атмосферного воздуха, температуру воздуха в ресивере; - учитывая, что масса одного кубического метра воздуха составляет 1,205 кг, определяют массу воздуха, сжимаемого в течение определённого времени работы компрессора
где T к - производительность компрессора, м3/мин; t к - время работы компрессора, мин; - при известной относительной влажности φ и температуре t в определяют действительное содержание влаги в 1 кг атмосферного воздуха, предварительно определив по графику, изображённому на рис. 1.6, максимальное содержание влаги
- определяют содержание влаги m сж в 1 кг сжатого до рабочего давления и охлаждённого до рабочей температуры t р воздуха при φ = 100 % по графику, изображённому на рис. 1.6; - так как m сж < m д, то остальная влага выпадает в виде жидкого конденсата m ж
Для измерения количества воздуха обычно используют объёмные единицы - литры или метры кубические. Учитывая, что объём, занимаемый одним и тем же количеством воздуха, может быть различным в зависимости от температуры и давления, его определяют при единых, или нормальных условиях. К нормальным условиям относят: - атмосферное давление р ат = 101325 Па (760 мм. рт. ст.); - температура 20 ºС (293,15 К); - относительная влажность φ = 65 %. Если объём рассчитан при нормальных условиях, то к его обозначению размерности добавляется слово «норм» (норм. л., норм. м3). Так, масса воздуха, содержащаяся в одном кубическом метре при нормальных условиях, составляет 1,205 кг. Если известно, что данное количество воздуха занимает некоторый объём W при давлении p и температуре t, то объём W норм, занимаемый этим же количеством воздуха при нормальных условиях, определяют по формуле:
Давление р в формуле (17) выражено в Паскалях, температура - в Кельвинах (1 К = – 273 ºС). Модели жидкостей Движение жидкости - это достаточно сложное перемещение отдельных её частиц, и вывести законы, описывающие это движение, для аналитической гидравлики оказалось очень сложной задачей. К тому же жидкость обладает различными физическими свойствами, изменение параметров которых от точки к точке может изменяться как угодно. Поэтому в гидравлике широко используют различные упрощённые модели жидкостей и отдельных явлений. При построении математической модели жидкости учитывают только те физические свойства, которые являются определяющими при решении данной задачи. Другие малозначимые свойства этой жидкости игнорируются. Это значительно упрощает математическое описание движения жидкости. Основой для большинства выведенных закономерностей в гидравлике послужили две наиболее значимые модели реальной жидкости: - модель идеальной (невязкой) несжимаемой жидкости. Эта модель характеризуется отсутствием касательных напряжений (сил вязкости), отсутствием какой - либо теплопроводности (теплообмена) и абсолютно несжимаема, то есть при течении такой жидкости выполняется закон сохранения энергии потока жидкости. Эта модель была предложена Д. Бернулли и Л. Эйлером. Следствием этого было сформулированное Д. Бернулли в 1738 году уравнение движения жидкости, связывающее между собой давление и скорость потока, названное позднее его именем. Уравнение Бернулли является основным в гидродинамике, и применяется при расчётах трубопроводов, насосов, турбин, компрессоров, при решении вопросов, связанных с фильтрацией и т. д. На основе такой модели Л. Эйлер вывел уравнение для течения жидкости в межлопаточном пространстве лопастного колеса (турбины), предложил способ описания движения жидкости; - модель вязкой несжимаемой жидкости. Такая модель очень близка к реальной жидкости, и позволяет получить систему дифференциальных уравнений, описывающих её поведение. Поскольку жидкость считается несжимаемой, то её плотность неизменна и распределена равномерно по объёму. Эта модель была предложена А. Навье в 1822 году и Д. Стоксом в 1845 году. Результатом этого явилось сформулированное уравнение, названное уравнением Навье - Стокса, являющееся одним из важнейших в гидродинамике. Оно применяется в моделировании многих природных явлений и технических задач, в частности: - описание течения в мантии Земли («проблема динамо» - взаимодействие между крутящимся вихревым потоком расплавленного материала во внешнем ядре Земли и магнитным полем); - описание воздушных масс атмосферы, в частности, при формировании прогноза погоды; - поведение многокомпонентных смесей жидкости; - описание конвективного тепломассообмена и т. д. Для описания движения газов используется модель идеальной (невязкой) сжимаемой жидкости. При рассмотрении явлений, протекающих в жидкости и при решении практических задач, прибегают к различным видам моделей жидкости на основе идеальной или вязкой модели. Так, для описания движения потока жидкости вводят понятие струйной модели, при рассмотрении турбулентного потока - двухслойной модели потока, для каналов, имеющих достаточную протяжённость - модель одномерного потока, прибегают к математическому моделированию работы гидротехнических сооружений (например, моделирование работы водопропускных труб и малых мостов) и т. д. Примеры решения задач Решение задач по определению параметров жидкости, основанных на её физических свойствах, не представляет больших трудностей. Решение подобных задач основано на понимании сущности свойств жидкости и применении формул, используемых при определении параметров жидкостей. В том случае, если необходимо определить плотность жидкости при изменении давления, предлагается самостоятельно вывести формулу для определения изменения плотности по аналогии с (1.10). Достаточно часто встречается случай, когда давление жидкости в полностью заполненном резервуаре, ёмкости или трубопроводе повышается вследствие повышения температуры (например, нагревание полностью заполненной водой ёмкости на солнце) или при подаче дополнительного объёма жидкости (например, при опрессовке трубопровода или при гидроударе - при резком закрытии крана или задвижки). В этом случае с учётом того, что конструкция резервуара, ёмкости или трубопровода принимается абсолютно жёсткой (отсутствует деформация корпуса), то такие задачи при применении формул (1.5) и (1.8) не имеют решения, так как при неизменных начальном и конечном объёмах (W 1 = W 2) коэффициенты βр и βt будут равны нулю. Для решения подобных задач введём понятие «условного объёма».
а) б) Рис. 1.7. Схема для определения физических свойств жидкости при неизменном объёме: а) - температурное расширение; б) - объёмное сжатие
Рассмотрим абсолютно жёсткий резервуар объёмом W 1, в котором жидкость находится при температуре t 1 (рис. 1.7, а). Будем считать, что при увеличении температуры до значения t 2 объём жидкости увеличился до некоторого условного объёма W 2 = W 1 + ∆ W. В этом случае в формуле (1.8) существует первоначальный объём W 1 и конечный объём W 2. Увеличение объёма на величину ∆ W вызовет увеличение давления на величину ∆ р. Поскольку конструкцию будем считать абсолютно жёсткой, то в данном случае увеличение давления будет происходить за счёт уменьшения условного объёма (W 1 + ∆ W) на величину ∆ W (рис. 1.7, б). Поэтому первоначальный объём - это условный объём (W 1 + ∆ W), конечный - это реальный объём W 1. В связи с этим формула (1.5) примет несколько иной вид:
Задача 1.7.1. При гидравлическом испытании трубопровода диаметром d = 200 мм и длиной L = 250 м давление в трубе было повышено до 3 МПа. Через час давление снизилось до 2 МПа. Сколько воды вытекло через неплотности, если модуль объёмной упругости Е 0 = 2060 МПа? Первоначальный объём воды в трубопроводе:
Изменение давления за час составит ∆ р = 3 – 2 = 1 МПа. Пользуясь формулами (1.5) и (1.6), определим уменьшение объёма воды ∆ W, которое вызвало уменьшение давления (знак «–» в формуле отбросим, учитывая, что объём воды уменьшается):
Задача 1.7.2. Трубопровод диаметром d = 500 мм и длиной L = 1 км наполнен водой при давлении 0,4 МПа и температуре воды 5 ºС. Определить, пренебрегая деформациями и расширением стенок трубы, давление в трубопроводе при нагревании воды в нём до 15 ºС, если модуль объёмной упругости Е 0 = 2060 МПа, а коэффициент температурного расширения βt = 0,15∙10-3 1/ ºС. Объём воды в трубопроводе:
Увеличение объёма воды ∆W при изменении температуры на величину ∆t = 15 – 5 = 10 ºС находим из (1.8):
Найдём увеличение давления ∆ р в связи с увеличением объёма воды ∆W, пользуясь понятием условного объёма, так как в реальности увеличение давления происходит без изменения объёма, с помощью формул (1.6) и (1.18):
Найдём давление в трубопроводе рt после увеличения температуры на 10 ºС: р t = р 0 + ∆ р = 400000 + 3080000 = 3,48 МПа. Задача 1.7.3. Сосуд заполнен водой, занимающей объём W = 2 м3. На сколько уменьшится и чему будет равен этот объём при увеличении давления на величину 200 бар при температуре 20 ºС? Модуль объёмной упругости для воды при данной температуре Е 0 = 2110 МПа. Изменение объёма жидкости определим из уравнения (1.5):
Коэффициент объёмного сжатия определим из уравнения (1.6):
Увеличение давления ∆ р = 200 бар = 20·
Искомый конечный объём будет равен: W кон = W – ∆W = 1,981 м3. Задача 1.7.4. Канистра, заполненная бензином и не содержащая воздуха, нагрелась на солнце до температуры 50 ºС. На сколько повысилось бы давление бензина внутри канистры, если бы она была абсолютно жёсткой? Начальная температура бензина 20 ºС. Модуль объёмной упругости бензина принять равным Е 0 =1300 МПа, коэффициент температурного расширения βt = 8 ∙ Из уравнения (1.8) находим относительное изменение объёма бензина при увеличении температуры ∆ t на 30 ºС (∆t = t 2 – t 1 = 30 ºС):
∆W = 0,024 W. Найдём увеличение давления ∆ р при увеличении температуры ∆ t на 30 ºС, пользуясь понятием условного объёма, так как увеличение давления происходит без изменения объёма, с помощью формул (1.6) и (1.18):
Задача 1.7.5. Плотность масла АМГ-10 при температуре 20 ºС составляет 850 кг/м3. Определить плотность масла при повышении температуры до 60 ºС и увеличении давления с атмосферного р 1 = 0,1 МПа до р 2 = 8,7 МПа. Модуль объёмной упругости масла Е 0 =1305 МПа, температурный коэффициент βt = 0,0008 (1/град). Плотность масла ρI при повышении температуры до значения t 2 = 60 ºС вычислим по формуле (1.10):
Плотность масла при повышении давления до значения p 2 = 8,7 МПа определим, исходя из утверждения, что при уменьшении объёма масса жидкости m ж не изменяется:
где W 1 - объём масла при повышении температуры до значения t 2 = 60 ºС; ∆W - объём, на который уменьшится объём W 1 до значения W 2 = W 1 – ∆W. Подставив в уравнение (1.19) выражение для ∆W (из формулы 1.5 ∆W = βрW 1∆ р), получим:
Задача 1.7.6. Определить объёмный модуль упругости жидкости, если под действием груза А массой 250 кг поршень прошел расстояние ∆h = 5 мм. Начальная высота положения поршня (без груза) H = 1,5 м; диаметр поршня d = 80 мм и резервуара D = 300 мм; высота резервуара h = 1,3 м. Весом поршня пренебречь. Резервуар считать абсолютно жёстким.
Рис. 1.8. Схема к задаче 1.7.6 Сила тяжести, создаваема грузом А, будет равна: F = m g = 2450 Н. Давление, создаваемое этой силой (т.е. приращение давления ∆ р), определим как:
Первоначальный объём W 1 жидкости равен:
Изменение объёма равно:
Модуль объёмной упругости определим, используя формулы (1.5) и (1.6):
Задача 1.7.7. Компрессор, имеющий производительность T к = 1,8 норм. м3/мин, сжимает воздух до 8 бар. Температура атмосферного воздуха на входе в компрессор составляет t в = 20 ºС, относительная влажность равна φ = 70 %. В ресивере сжатый воздух охлаждается до 25 ºС. Сколько воды выпадает в ресивере в течение часа? Учитывая, что 1 норм. м3 воздуха имеет массу 1,205 кг, масса воздуха, сжимаемого в течение часа
По графику (рис. 1.6) находим, что содержание влаги в 1 кг насыщенного воздуха при атмосферном давлении (на графике это линия при 0,00 МПа) и температуре 20 ºС составляет 15 г. При относительной влажности φ = 70 % содержание влаги в 1 кг воздуха составит
Содержание влаги в 1 кг воздуха, сжатого до 8 бар и охлаждённого до 25 ºС при относительной влажности φ = 100 %, согласно графику (рис. 1.6), составляет 2,4 г. Отсюда следует, что «лишняя» влага выпадает в виде конденсата. Количество конденсата, выпадающего из 1 кг сжатого воздуха
Количество конденсата, выпадающего в течение часа, составит
Гидростатика Примеры решения задач При решении задач по гидростатике необходимо различать такие понятия, как давление р и сила давления Р. Если давление р зависит только от высоты столба жидкости, то сила давления Р определяется площадью поверхности S, на которое по нормали действует давление жидкости: Р = рS. Применяя основное уравнение гидростатики, нужно помнить, что второй член в правой части уравнения может быть как положительным, так и отрицательным. Необходимо твёрдо различать давления абсолютное, избыточное (манометрическое) и вакуумметрическое, а также весовое давление столба жидкости ρ g h. Очевидно, что при увеличении высоты столба жидкости давление увеличивается, а по мере подъёма к свободной поверхности жидкости - уменьшается. Необходимо четко представлять, что пъезометрическая высота При решении задач, в которых даны поршни или системы поршней, следует составить уравнение равновесия, то есть равенство нулю суммы всех сил, действующих на поршень или систему поршней. В задачах на относительный покой жидкости следует учитывать повышение давления за счёт силы инерции переносного движения. Положение свободной поверхности жидкости в сосуде при заданной угловой скорости вращения определяется объёмом находящейся в ней жидкости. При этом используется формула объёма параболоида вращения W п:
где R - радиус основания параболоида; h - высота параболоида. Если угловая скорость вращения достаточно большая, то силой тяжести жидкости можно пренебречь и повышение давления следует определять по формуле (2.13). Сила давления жидкости на плоскую стенку зависит от положения центра тяжести hС и центра давления hD площадки. Численное значение силы давления жидкости на плоскую стенку определяют по формуле (2.18). В случае необходимости определения какой - либо внешней силы необходимо составить уравнение моментов всех действующих сил, правильно учитывая плечи этих сил относительно выбранного центра. Если стенка находится в жидкости на некоторой глубине, то глубина погружения центра тяжести будет определяться как сумма собственно центра тяжести площадки и высоты столба жидкости от верхней точки площадки до свободной поверхности жидкости. Глубину погружения центра давления в этом случае определяют по соответствующим формулам, приводимым в учебниках и справочниках по гидравлике. В данном пособии этот вопрос не рассмативается. При определении силы давления жидкости на криволинейную поверхность необходимо помнить, что значение этой силы складывается из горизонтальной (сила давления жидкости на вертикальную проекцию данной стенки) и вертикальной (вес жидкости в объёме, заключенном между данной криволинейной стенкой, свободной поверхностью жидкости и вертикальной проекции стенки) составляющих, и определяется по формуле (2.19). Задача 2.7.1. В цилиндрический бак диаметром d = 2 м до уровня h = 1,5 м налиты вода и бензин. Уровень воды в пьезометре, открытом в атмосферу, ниже уровня бензина на h п = 300 мм. Определить объём находящегося в баке бензина, если плотность бензина ρ б = 700 кг/м3, плотность воды ρ в = 1000 кг/м3.
Рис. 2.17. Схема к задаче 2.7.1
Исходя из схемы подключения пъезометра, можно утверждать, что давление на дне бака и в нижней части пъезометра (точки А и В, рис. 2.17) будет одинаковым: рА = рВ. Составим основное уравнение гидростатики, где весовое (избыточное) давление воды и бензина в баке будет равно весовому давлению воды в пьезометре:
где h в и h б - высота воды и бензина в баке соответственно. Поскольку в этом уравнении два неизвестных (высоты h в и h б), выразим h в = h – h б, и подставим:
После сокращения получим:
Объём находящегося в баке бензина:
Задача 2.7.2. Определить абсолютное давление р 0 воздуха на свободной поверхности воды в напорном баке по показанию ртутного манометра. Какой высоты h п должен быть уровень воды в пьезометре для измерения того же давления р 0? Высоты h = 2,6 м; h 1 = 1,8 м; h 2 = 0,6 м. Плотность ртути ρ = 13600 кг/м3, воды ρ = 1000 кг/м3. Атмосферное давление составляет 765 мм. рт. ст.
Рис. 2.18. Схема к задаче 2.7.2
Составим основное уравнение гидростатики в абсолютных величинах давлений. Из анализа схемы, изображённой на рис. 2.18, видно, что давление в ртутном пъезометре на линии А, образованное за счёт весового давления столба ртути (h 1 – h 2) и атмосферного давления, будет уравновешено весовым давлением воды ρ вg(h – h 2) и абсолютным давлением р 0, действующим на свободной поверхности воды в баке:
Для нахождения высоты h п рассуждаем аналогично: весовое давление воды ρ вg h в баке и абсолютное давление р 0, действующее на свободной поверхности, будут уравновешены весовым давлением ρ вg h п воды в пъезометре и атмосферным давлением:
Задача 2.7.3. Определить силу F, действующую на шток гибкой диафрагмы гидроцилиндра, если её диаметр d = 200 мм, показание манометра р м = 0,27 МПа, высота h = 1 м. Площадью штока пренебречь. Найти абсолютное давление в левой полости, если h aт = 740 мм. рт. ст. Плотность жидкости составляет ρ = 850 кг/м3.
Рис. 2.19. Схема к задаче 2.7.3
Сила F, действующая по оси гидроцилиндра, создаёт избыточное давление р изб, действующее на стенки гидроцилиндра. Давление определим по показанию манометра с учётом высоты столба жидкости h:
Сила, действующая на шток диафрагмы:
Атмосферное давление составляет:
Абсолютное (с учётом атмосферного)давление в левой полости:
Задача 2.7.4. Система из двух поршней, соединенных штоком, находится в равновесии. Определить силу, сжимающую пружину. Жидкость, находящаяся между поршнями и в бачке - масло с плотностью ρ = 870 кг/м3. Диаметры D = 80 мм; d = 30 мм; высота h = 1000 мм; избыточное давление р 0 = 10 кПа. Избыточное давление, действующее на кольцевую поверхность поршней, будет равно:
Рис. 2.20. Схема к задаче 2.7.4
Силы F 1 и F 2, действующие на кольцевые площади поршней с диаметрами D = 80 мм и d = 30 мм, будут равны:
Сила, сжимающая пружину, будет равна:
Задача 2.7.5. Определить силу F, необходимую для удержания в равновесии поршня, если труба под поршнем заполнена водой плотностью ρ = 1000 кг/м3. Размеры трубы d = 100 мм, h 1 = 4 м, h 2 = 0,5 м. Длина рычага а = 0,2 м, b =1 м. Собственным весом поршня пренебречь.
Рис. 2.21. Схема к задаче 2.7.5
Логично предположить, что сила F, необходимая для удержания поршня в равновесии, должна соответствовать избыточному давлению под ним, то есть весовому давлению столба жидкости:
Сила на штоке F ш, необходимая для его удержания в равновесии:
Сила F в соответствии с длинами плеч рычага равна:
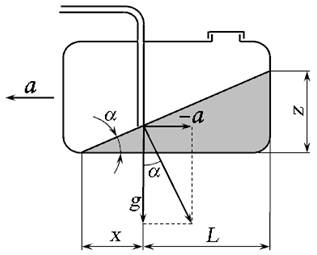
Задача 2.7.6. Автомобиль движется с ускорением а = 3,27 м/с2. Определить минимальное количество топлива в баке, обеспечивающее его подачу без подсоса воздуха. Считать, что бензопровод установлен на расстоянии L = 0,45 м от задней стенки бака, диаметр бензопровода мал по сравнению с длиной бака, высота h = 10 мм. Ширина бака b = 0,5 м, плотность бензина ρ = 750 кг/м3. Определить избыточное давление, оказываемое на заднюю стенку бензобака.
а) б) Рис. 2.22. Схема к задаче 2.7.6
Изобразим положение бензина в баке с минимальным объёмом (рис. 2.22, б). Обозначим стороны прямоугольного треугольника как (x + L) и z. Тогда:
Объём минимального количества бензина в баке, обеспечивающего его подачу без подсоса, будет равно:
Давление, оказываемое на заднюю стенку бензобака, определим по формуле (2.15):
Задача 2.7.7. На рисунке показана одна из возможных схем гидроусилителя сцепления автомобиля. Масло под давлением р 0 = 0,5 МПа подводится внутри
|
||||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 1805; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.018 с.) |


 , (1.16)
, (1.16)

 ,
, в 1 кг воздуха при известной температуре t в и атмосферном давлении
в 1 кг воздуха при известной температуре t в и атмосферном давлении ;
; .
. . (1.17)
. (1.17)
 . (1.18)
. (1.18) = 7,85 м3.
= 7,85 м3. = 0,00381 м3 = 3,81 л.
= 0,00381 м3 = 3,81 л. = 196,25 м3.
= 196,25 м3. = 0,294 м3.
= 0,294 м3. = 3081447,4 Па = 3,08 МПа.
= 3081447,4 Па = 3,08 МПа. .
. = 4,74·
= 4,74·  1/Па.
1/Па. Па. Тогда:
Па. Тогда: = 0,019 м3.
= 0,019 м3. 1/град.
1/град. = 0,024;
= 0,024; = 30,48МПа.
= 30,48МПа. = 823,6 кг/м3.
= 823,6 кг/м3.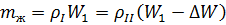 , откуда
, откуда 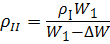 , (1.19)
, (1.19) = 829 кг/м3.
= 829 кг/м3.
 = 490 кПа.
= 490 кПа.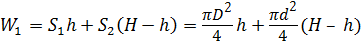 = 0,093 м3.
= 0,093 м3. м3.
м3. Па =1814 МПа.
Па =1814 МПа. = 130 кг.
= 130 кг. = 10,5 г.
= 10,5 г. = 8,1 г.
= 8,1 г. = 1053 г.
= 1053 г. - это высота столба жидкости в пъезометре (пъезометр – это стеклянная трубка, манометр жидкостного типа для измерения избыточного давления).
- это высота столба жидкости в пъезометре (пъезометр – это стеклянная трубка, манометр жидкостного типа для измерения избыточного давления). , (2.20)
, (2.20)
 ,
, .
. , откуда высота бензина в баке
, откуда высота бензина в баке = 1м.
= 1м. = 3,14 м3.
= 3,14 м3.
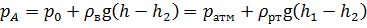 , откуда
, откуда
 =
= = 242310,5 Па = 0,24 МПа.
= 242310,5 Па = 0,24 МПа. , откуда
, откуда = 16,92 м.
= 16,92 м.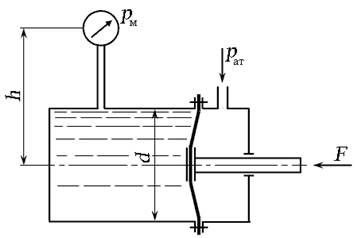
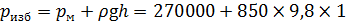 = 278330 Па.
= 278330 Па.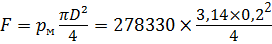 = 8740 Н = 8,74 кН.
= 8740 Н = 8,74 кН. = 98642 Па.
= 98642 Па.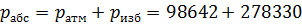 = 376972 Па = 0,377 МПа.
= 376972 Па = 0,377 МПа.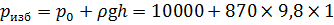 = 18526 Па.
= 18526 Па.
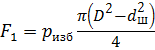 ,
, .
. = 79,87 Н.
= 79,87 Н.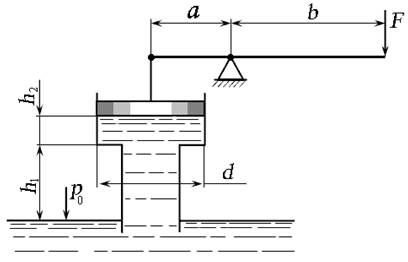
 = 44100 Па.
= 44100 Па. = 346,2 Н
= 346,2 Н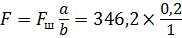 = 69,24 Н.
= 69,24 Н.
 = 0,33367, α = 18,45 град.
= 0,33367, α = 18,45 град. = 0,3 м,
= 0,3 м, = 0,25 м.
= 0,25 м. = 0,047 м3 = 47 л.
= 0,047 м3 = 47 л. = 2573,25 Па.
= 2573,25 Па.


