Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гидродинамическое воздействие струи на твёрдую преградуСодержание книги
Поиск на нашем сайте При воздействии струи жидкости на любую твёрдую преграду сила давления жидкости Р равна произведению гидродинамического давления на площадь действия. Для определения силы Р используют теорему количества движения - изменение количества движения ∆mV равно импульсу внешних сил ∆F, приложенных к выделенному участку потока:
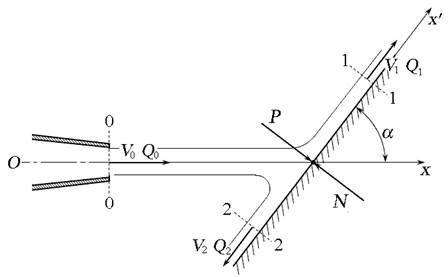
Рассмотрим неподвижную плоскую стенку, расположенную под углом α относительно оси струи (рис. 5.7). Струя жидкости вытекает из насадка площадью S 0 с расходом Q 0 и скоростью истечения V 0. Со стороны стенки возникает противодействующая сила N, равная силе давления жидкости Р и направленная в противоположную сторону:
Рис. 5.7. Схема воздействия струи на твёрдую преграду
Изменение количества движения (∆mV) за время dt в проекции на ось ОХ будет равно:
где Импульс внешних сил за время dt равно
Учитывая, что
Расход в сечении 0 - 0 за время dt равен сумме расходов в сечениях 1 - 1 и 2 - 2:
Определим расходы в сечениях 1 - 1 и 2 - 2. Для этого запишем уравнение количества движения относительно оси х′, проходящей по наклонной плоской стенке. Учитывая, что силы P и N направлены по нормали к выбранной оси х ′, проекция сил на эту ось будет равна нулю. Тогда:
откуда Используя уравнение равенства расходов, получим следующие значения расходов Q 1 и Q 2:
Подставим расходы Q 1 и Q 2 в уравнение (5.12), учитывая, что скорости в сечениях V 0 = V 1 = V 2:
После математических преобразований получим:
Учитывая, что
Если поверхность, на которую действует струя жидкости, движется в направлении движения жидкости со скоростью V пов, сила давления жидкости будет равна:
Рассмотрим реактивное действие струи, истекающей из сопла центробежного масляного фильтра (рис. 5.8).
Рис. 5.8. Схема двухсопловой центрифуги с гидрореактивным приводом
Согласно теореме количества движения, реактивная сила при вращении вала фильтра согласно (5.16) с учётом α = 90º,
Вращающий момент на валу фильтра:
Учитывая, что расход масла Q, поступающего в центрифугу, равен Примеры решения задач Задачи на истечение решают без составления уравнения Бернулли с помощью основного выражения (5.4) или (5.6). При этом следует помнить, что гидростатический напор H ст определяется разностью давлений до и после отверстия. При расчёте истечения через насадки следует помнить, что коэффициенты истечения в отличие от истечения через отверстие определяют по табл. 3. Задача 5.3.1. Определить расход и скорость истечения воды из малого круглого отверстия диаметром d 0 = 3 см в боковой стенке резервуара больших размеров. Напор над центром отверстия h = 1 м, кинематическая вязкость воды при t = 20 ºС составляет ν = 10-6 м2/с. Определим число Рейнольдса, характеризующее истечение без учёта коэффициента скорости φ, то есть для истечения без образования сжатого сечения и сопротивления:
Из рис. 5.2 при Rе = 133 000 определим коэффициенты скорости φ и расхода μ р: φ = 0,98; μ р = 0,59. Тогда скорость истечения воды из малого отверстия в тонкой стенке в сжатом сечении будет равна:
Расход вытекающей из отверстия воды будет равен:
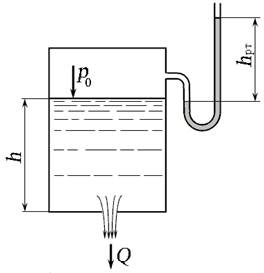
Задача 5.3.2. Определить расход жидкости, вытекающей из бака через отверстие площадью S 0 = 0,01 см2. Показание ртутного манометра h рт = 268 мм, высота h = 2 м, коэффициент расхода отверстия μ р = 0,60. Плотность жидкости в баке ρ = 800 кг/м3, плотность ртути ρ рт = 13600 кг/м3. Атмосферное давление р ат = 0,1 МПа. Напор считать постоянным. Определить, во сколько раз увеличится расход, если к отверстию присоединить цилиндрический внешний насадок, конически расходящийся насадок длиной L н = 5 d 0 при угле конусности γ = 7º. Расход жидкости определим по формуле (5.7): Перепад давления ∆ р с верхней и нижней стороны отверстия определим в абсолютных единицах. Тогда ∆ р будет равен разности давления на дне сосуда (сумма р 0и весового давления
Рис. 5.7. Схема к задаче 5.3.2
Давление р 0 (абсолютное давление) определим по показанию ртутного пъезометра, высота столба ртути в котором уравновесит избыточное давление, действующее по свободной поверхности жидкости в баке. Тогда абсолютное давление р 0 будет равно:
Тогда перепад давления:
Расход жидкости через малое отверстие в тонкой стенке будет равен:
Определим расход жидкости при присоединении насадка к отверстию диаметром d 0, который равен - цилиндрический внешний насадок (μ внеш = 0,82)
- конически расходящийся насадок (μ к.р. = 0,5 по S вых)
Определим, во сколько раз расход через насадки больше, чем через отверстие в тонкой стенке: - через цилиндрический насадок - через расходящийся насадок Задача 5.3.3. Определить направление истечения жидкости с плотностью ρ = 1000 кг/м3 через отверстие диаметром d 0 = 5 мм и расход, если разность уровней h = 2 м, показание вакуумметра соответствует 147 мм. рт. ст., показание манометра p м = 0,25 МПа, коэффициент расхода μ р = 0,62.
Рис. 5.8. Схема к задаче 5.3.3
Разность избыточного давления между баками равна:
Поскольку давление в правой части бака больше, чем в левой, то направление течения жидкости будет направлено в левую часть емкости (ответ получили со знаком «+», Тогда расход жидкости через отверстие с диаметром d 0 будет равен:
Задача 5.3.4. Определить диаметр отверстия дросселя d 0, установленного на сливе из гидроцилиндра, если шток цилиндра под действием внешней нагрузки F = 60 кН перемещается вправо со скоростью V = 20 см/с. Диаметры штока d ш = 40 мм, поршня D = 80 мм, коэффициент расхода дросселя μ р = 0,65, плотность жидкости ρ = 850 кг/м3 , давление на сливе р с = 0,3 МПа.
Рис. 5.9. Схема к задаче 5.3.4 Определим избыточное давление в жидкости, которое создает сила F в правой части гидроцилиндра. Давление создаётся эффективной площадью поршня (эффективная площадь
Перепад давлений на дросселе ∆ р будет равен: ∆ р = р – р с = 15,7 МПа. Расход жидкости, протекающий через живое сечение дросселя рабочей площадью S 0 со скоростью V др, будет равен расходу в цилиндре площадью S эф со скоростью V:
Площадь рабочего сечения дросселя S др будет равна:
Тогда диаметр отверстия дросселя:
Расчёт трубопровода Трубопроводом называют систему напорных труб, предназначенных для перемещения разнообразных жидкостей и газов. Движение жидкости или газа по трубопроводу происходит в результате того, что напор в его начале больше, чем в конце.
а) б)
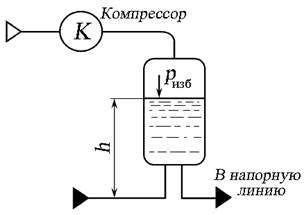
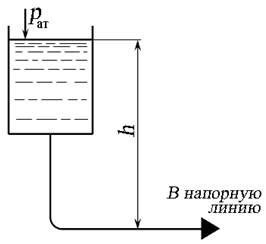
в) г) Рис. 6.1. Создание напора с помощью: а) - насоса; б) - давления газа; в) - водонапорной башни; г) - разности высот уровней жидкости
Пъезометрический напор H п в трубопроводе может быть создан: - за счёт работы насосов различного типа (рис. 6.1, а), - избыточным давлением газа в резервуаре с жидкостью с помощью компрессора (рис. 1.6, б), - использованием водонапорной башни (рис. 1.6, в), - за счёт разности высот уровней жидкости в сообщающихся сосудах (рис. 1.6, г), где ph и p∆h - избыточное давление, создаваемое высотой столба жидкости h и ∆h соответственно. В зависимости от компоновки и технического расположения трубопроводы подразделяют на простые и сложные. Простым называется трубопровод без ответвлений, состоящий из труб одного диаметра. Простой трубопровод разделяют на короткий и длинный. К длинным относят трубопроводы значительной протяжённости, в которых потери напора по длине являются основными, а местные потери напора составляют не более 10 % от общих потерь. К таким трубопроводам относят магистральные трубопроводы, газопроводы, трубопроводы гидротехнических сооружений. В технических гидроприводах (например, станочные гидроприводы, гидроприводы автомобильных систем) применяют короткие трубопроводы, в которых местные потери соизмеримы с потерями по длине. Сложным называется трубопровод, состоящий из труб разного диаметра, соединённых последовательно, параллельно или разветвлено.
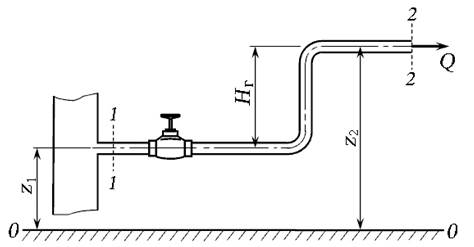
Потребный напор Рассмотрим простой трубопровод, в котором напор создан избыточным давлением р 1 в сечении 1 - 1 (рис. 6.2).
Рис. 6.2. Схема к определению потребного напора
Составим уравнение Бернулли для сечений 1 - 1 и 2 - 2 относительно произвольно выбранной плоскости сравнения 0 - 0:
Трубопровод не меняет своего диаметра, поэтому V 1 = V 2 = V. Принимаем течение жидкости в трубопроводе турбулентным, коэффициент Кориолиса α 1 = α 2 = 1. Геометрическую высоту поднятия жидкости в трубопроводе обозначим как геометрический напор H г:
Тогда уравнение (6.1) примет вид:
Сумма
Потери напора h пот выразим через расход Q (п. 4.1, 4.2):
где m - показатель степени (m = 1 при ламинарном течении, m = 2 при турбулентном течении); K - величина сопротивления трубопровода. Параметр K является размерной величиной, и для турбулентного режима равен:
Пъезометрический напор Потребный напор H потр - это пъезометрический напор, затрачиваемый на создание гидростатического напора H ст при заданном расходе Q:
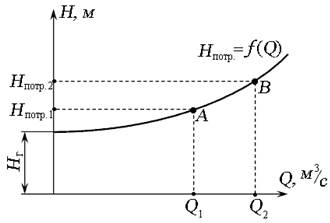
Используя выражение (6.3), можно построить графическую зависимость
Рис. 6.3. Кривая потребного напора
Зависимость потерь напора h пот от расхода Q называют гидравлической характеристикой трубопровода:
При ламинарном режиме гидравлическая характеристика трубопровода и кривая потребного напора представляют собой прямую линию (m = 1), при турбулентном течении - параболу второй степени (m = 2).
|
||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 4833; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

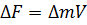 .
.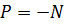 .
.
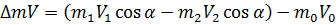 ,
,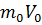 ,
, 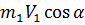 и
и 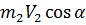 - проекции количества движения жидкости в сечениях 0 - 0, 1 - 1 и 2 - 2 на ось ОХ.
- проекции количества движения жидкости в сечениях 0 - 0, 1 - 1 и 2 - 2 на ось ОХ. . Тогда:
. Тогда: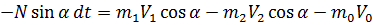 .
. , получим:
, получим: . (5.12)
. (5.12) .
. ,
, .
.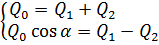 , откуда
, откуда 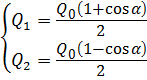 . (5.13)
. (5.13)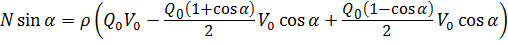 .
.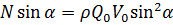 , откуда
, откуда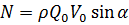 . (5.14)
. (5.14)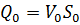 , сила давления жидкости на неподвижную плоскую твёрдую стенку будет равна:
, сила давления жидкости на неподвижную плоскую твёрдую стенку будет равна: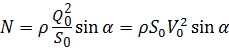 . (5.15)
. (5.15)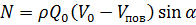 . (5.16)
. (5.16)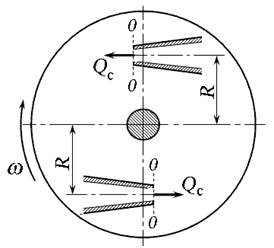
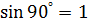 :
: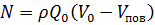 ,
,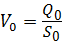 ,
, 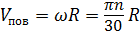 ,
,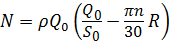 .
.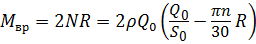 .
.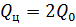 , окончательно получим
, окончательно получим 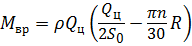 .
.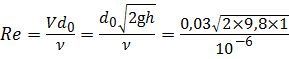 = 133000.
= 133000.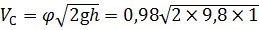 = 4,3 м/с.
= 4,3 м/с.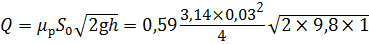 = 1,91 л/с.
= 1,91 л/с.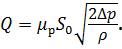
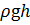 ) и атмосферного давления, то есть:
) и атмосферного давления, то есть: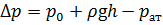 .
.
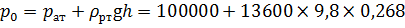 = 135,72 кПа.
= 135,72 кПа.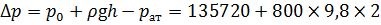 = 51,4 кПа.
= 51,4 кПа.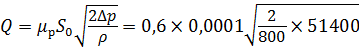 = 0,68 л/с.
= 0,68 л/с.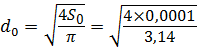 = 0,011 м:
= 0,011 м: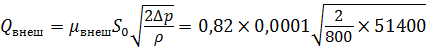 = 0,93 л/с;
= 0,93 л/с;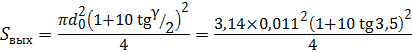 = 0,000247 м2,
= 0,000247 м2,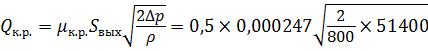 = 1,4 л/с.
= 1,4 л/с.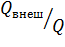 = 1,37 раза;
= 1,37 раза;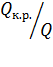 = 2,06 раза.
= 2,06 раза.
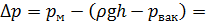
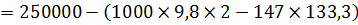 = 250 кПа.
= 250 кПа.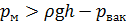 ).
).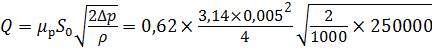 = 0,27 л/с.
= 0,27 л/с.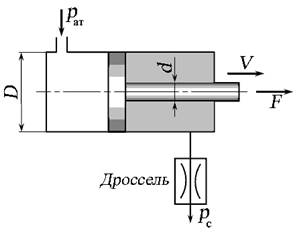
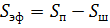 ):
):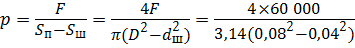 = 16 МПа.
= 16 МПа.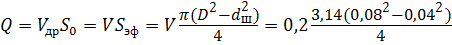 = 0,75 л/с.
= 0,75 л/с.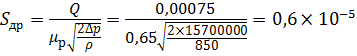 м2.
м2.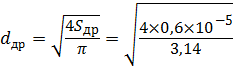 = 2,76 мм.
= 2,76 мм.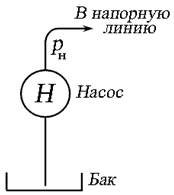
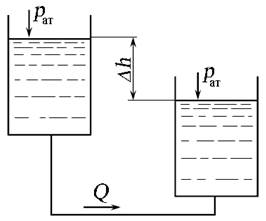
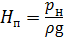 ;
;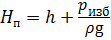 ;
;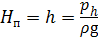 ;
;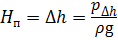 ,
,
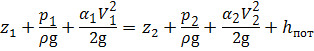 . (6.1)
. (6.1)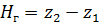 .
.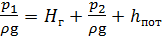 . (6.2)
. (6.2)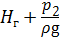 представляет собой гидростатический напор H ст жидкости в сечении 2 - 2:
представляет собой гидростатический напор H ст жидкости в сечении 2 - 2: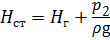 .
.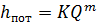 ,
,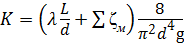 . (6.3)
. (6.3)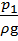 в сечении 1 - 1 необходим для обеспечения заданного расхода Q жидкости в трубопроводе. Такой напор называют потребным.
в сечении 1 - 1 необходим для обеспечения заданного расхода Q жидкости в трубопроводе. Такой напор называют потребным.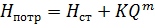 . (6.4)
. (6.4)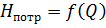 , которую называют кривой потребного напора (рис. 6.3). Построив кривую, можно определить необходимый потребный напор для любого заданного расхода (например, т. А и В).
, которую называют кривой потребного напора (рис. 6.3). Построив кривую, можно определить необходимый потребный напор для любого заданного расхода (например, т. А и В).