Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Давление покоящейся жидкости на ограничивающие её поверхностиСодержание книги
Похожие статьи вашей тематики
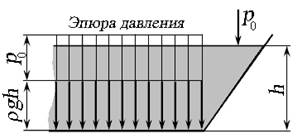
Поиск на нашем сайте Распределение давления по поверхности отражают в виде эпюр давления, построение которых основано на свойствах гидростатического давления. Эпюра давления - это графическое изображение распределения гидростатического давления в жидкости в зависимости от высоты столба жидкости. Давление представляется вектором, направление которого нормально к ограничивающей жидкость поверхности, а его значение определяется избыточным или абсолютным значением давления в точке приложения данного вектора.
Рис. 2.13. Действие гидростатического давления на горизонтальную плоскость
Давление жидкости на ограничивающие её горизонтальные поверхности определяется основным уравнением гидростатики (рис. 2.13):
Силу давления жидкости вызывает только избыточное давление:
где S - площадь поверхности, ограничивающей жидкость. Из формулы (2.16) видно, что сила давления на горизонтальную поверхность, ограничивающую жидкость, зависит от плотности жидкости ρ, высоты столба жидкости h, площади поверхности S, но не зависит от формы сосуда (рис. 2.14). В этом заключается так называемый гидростатический парадокс.
Рис. 2.14. Гидростатический парадокс
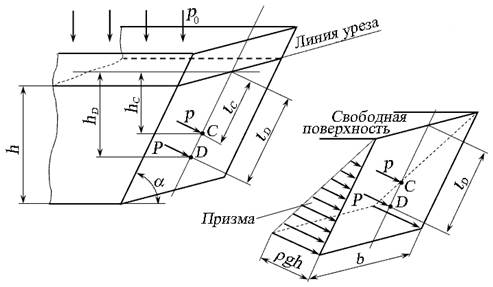
Определение силы давления жидкости на боковую поверхность в ряде случаев необходимо для прочностного расчёта конструкции. Боковая поверхность может быть плоской (вертикальной или наклонной) или цилиндрической формы. Сила давления жидкости на плоскую стенку. Задача по определению силы давления на плоскую стенку (поверхность, ограничивающую жидкость), сводится к определению равнодействующей силы давления (по величине и направлению), а также нахождению точки её приложения. Давление, действующее на боковую стенку, увеличивается по мере погружения (рис. 2.15). Характерной особенностью действия давления на боковую стенку является наличие центра тяжести и центра давления.
Рис. 2.15. Схема действия жидкости на плоскую стенку
Центр тяжести (точка С) - точка приложения давления р, вектор которого направлен по нормали к плоской стенке. Центр тяжести таких плоских фигур, как прямоугольник или круг, находится в центре их симметрии, то есть
Центр давления (точка D) - точка приложения силы давления Р, вектор которой также направлен по нормали к плоской стенке. Для определения координаты центра давления рассмотрим фигуру, образованную эпюрой давления. При действии на прямоугольную стенку эпюра давления представляет собой объёмную фигуру - призму. Сила давления на стенку равна весу жидкости в объёме фигуры, то есть сила давления определяется массой жидкости в объёме фигуры, построенной с помощью эпюры давления. Точка приложения силы давления при действии на плоскую стенку будет находиться на линии центра тяжести объёмной фигуры. Так как основанием призмы является прямоугольный треугольник, то центр тяжести призмы отстоит от вершины треугольника на 2/3 его высоты. Координата центра давления площадки hD:
Координата центра давления необходима для выполнения прочностных расчётов конструкций, ограничивающих жидкость. Cила давления:
где S - площадь плоской стенки. Таким образом, центр тяжести hС и центр давления hD не совпадают. Глубина погружения центра давления плоской стенки зависит от её конфигурации. Для некоторых различных плоских фигур выражения для определения центра тяжести hС и центра давления hD приведены в таб. 3. Таблица 3 Координата центра тяжести и центра давления для некоторых плоских фигур
Сила давления покоящейся жидкости на цилиндрическую поверхность. Определение силы давления жидкости на цилиндрическую поверхность имеет следующие особенности: - векторы сил давления, распределённые по криволинейной поверхности, не параллельны друг другу; - силу давления Р, приложенной к любой точке криволинейной поверхности (кроме направления вектора силы, действующей только по вертикали или только по горизонтали), можно разложить на две составляющие - горизонтальную Рх и вертикальную Рz
- горизонтальная сила Pх численно равна силе избыточного давления, приложенной к плоской вертикальной проекции криволинейной поверхности; - вертикальная сила Pz равна весу тела давления в объёме W
Рис. 2.16. Схема действия силы давления жидкости на криволинейную поверхность
Рассмотрим цилиндрический резервуар для перевозки жидкости (рис. 2.16). Вертикальной проекцией цилиндрической поверхности будет прямоугольник со стороной
где S - площадь плоской проекции. Объём жидкости, ограниченный криволинейной поверхностью, вертикальной проекцией криволинейной поверхности и свободной поверхностью жидкости при её наличии, называется телом давления. Иными словами, тело давления - это объём жидкости, опирающийся своим весом на криволинейную поверхность. Объём тела давления, изображённого на рис. 2.16, равен половине объёма цилиндра:
где L - длина цилиндра. Горизонтальная составляющая Px приложена к центру давления с вертикальной координатой hD =
Примеры решения задач При решении задач по гидростатике необходимо различать такие понятия, как давление р и сила давления Р. Если давление р зависит только от высоты столба жидкости, то сила давления Р определяется площадью поверхности S, на которое по нормали действует давление жидкости: Р = рS. Применяя основное уравнение гидростатики, нужно помнить, что второй член в правой части уравнения может быть как положительным, так и отрицательным. Необходимо твёрдо различать давления абсолютное, избыточное (манометрическое) и вакуумметрическое, а также весовое давление столба жидкости ρ g h. Очевидно, что при увеличении высоты столба жидкости давление увеличивается, а по мере подъёма к свободной поверхности жидкости - уменьшается. Необходимо четко представлять, что пъезометрическая высота При решении задач, в которых даны поршни или системы поршней, следует составить уравнение равновесия, то есть равенство нулю суммы всех сил, действующих на поршень или систему поршней. В задачах на относительный покой жидкости следует учитывать повышение давления за счёт силы инерции переносного движения. Положение свободной поверхности жидкости в сосуде при заданной угловой скорости вращения определяется объёмом находящейся в ней жидкости. При этом используется формула объёма параболоида вращения W п:
где R - радиус основания параболоида; h - высота параболоида. Если угловая скорость вращения достаточно большая, то силой тяжести жидкости можно пренебречь и повышение давления следует определять по формуле (2.13). Сила давления жидкости на плоскую стенку зависит от положения центра тяжести hС и центра давления hD площадки. Численное значение силы давления жидкости на плоскую стенку определяют по формуле (2.18). В случае необходимости определения какой - либо внешней силы необходимо составить уравнение моментов всех действующих сил, правильно учитывая плечи этих сил относительно выбранного центра. Если стенка находится в жидкости на некоторой глубине, то глубина погружения центра тяжести будет определяться как сумма собственно центра тяжести площадки и высоты столба жидкости от верхней точки площадки до свободной поверхности жидкости. Глубину погружения центра давления в этом случае определяют по соответствующим формулам, приводимым в учебниках и справочниках по гидравлике. В данном пособии этот вопрос не рассмативается. При определении силы давления жидкости на криволинейную поверхность необходимо помнить, что значение этой силы складывается из горизонтальной (сила давления жидкости на вертикальную проекцию данной стенки) и вертикальной (вес жидкости в объёме, заключенном между данной криволинейной стенкой, свободной поверхностью жидкости и вертикальной проекции стенки) составляющих, и определяется по формуле (2.19). Задача 2.7.1. В цилиндрический бак диаметром d = 2 м до уровня h = 1,5 м налиты вода и бензин. Уровень воды в пьезометре, открытом в атмосферу, ниже уровня бензина на h п = 300 мм. Определить объём находящегося в баке бензина, если плотность бензина ρ б = 700 кг/м3, плотность воды ρ в = 1000 кг/м3.
Рис. 2.17. Схема к задаче 2.7.1
Исходя из схемы подключения пъезометра, можно утверждать, что давление на дне бака и в нижней части пъезометра (точки А и В, рис. 2.17) будет одинаковым: рА = рВ. Составим основное уравнение гидростатики, где весовое (избыточное) давление воды и бензина в баке будет равно весовому давлению воды в пьезометре:
где h в и h б - высота воды и бензина в баке соответственно. Поскольку в этом уравнении два неизвестных (высоты h в и h б), выразим h в = h – h б, и подставим:
После сокращения получим:
Объём находящегося в баке бензина:
Задача 2.7.2. Определить абсолютное давление р 0 воздуха на свободной поверхности воды в напорном баке по показанию ртутного манометра. Какой высоты h п должен быть уровень воды в пьезометре для измерения того же давления р 0? Высоты h = 2,6 м; h 1 = 1,8 м; h 2 = 0,6 м. Плотность ртути ρ = 13600 кг/м3, воды ρ = 1000 кг/м3. Атмосферное давление составляет 765 мм. рт. ст.
Рис. 2.18. Схема к задаче 2.7.2
Составим основное уравнение гидростатики в абсолютных величинах давлений. Из анализа схемы, изображённой на рис. 2.18, видно, что давление в ртутном пъезометре на линии А, образованное за счёт весового давления столба ртути (h 1 – h 2) и атмосферного давления, будет уравновешено весовым давлением воды ρ вg(h – h 2) и абсолютным давлением р 0, действующим на свободной поверхности воды в баке:
Для нахождения высоты h п рассуждаем аналогично: весовое давление воды ρ вg h в баке и абсолютное давление р 0, действующее на свободной поверхности, будут уравновешены весовым давлением ρ вg h п воды в пъезометре и атмосферным давлением:
Задача 2.7.3. Определить силу F, действующую на шток гибкой диафрагмы гидроцилиндра, если её диаметр d = 200 мм, показание манометра р м = 0,27 МПа, высота h = 1 м. Площадью штока пренебречь. Найти абсолютное давление в левой полости, если h aт = 740 мм. рт. ст. Плотность жидкости составляет ρ = 850 кг/м3.
Рис. 2.19. Схема к задаче 2.7.3
Сила F, действующая по оси гидроцилиндра, создаёт избыточное давление р изб, действующее на стенки гидроцилиндра. Давление определим по показанию манометра с учётом высоты столба жидкости h:
Сила, действующая на шток диафрагмы:
Атмосферное давление составляет:
Абсолютное (с учётом атмосферного)давление в левой полости:
Задача 2.7.4. Система из двух поршней, соединенных штоком, находится в равновесии. Определить силу, сжимающую пружину. Жидкость, находящаяся между поршнями и в бачке - масло с плотностью ρ = 870 кг/м3. Диаметры D = 80 мм; d = 30 мм; высота h = 1000 мм; избыточное давление р 0 = 10 кПа. Избыточное давление, действующее на кольцевую поверхность поршней, будет равно:
Рис. 2.20. Схема к задаче 2.7.4
Силы F 1 и F 2, действующие на кольцевые площади поршней с диаметрами D = 80 мм и d = 30 мм, будут равны:
Сила, сжимающая пружину, будет равна:
Задача 2.7.5. Определить силу F, необходимую для удержания в равновесии поршня, если труба под поршнем заполнена водой плотностью ρ = 1000 кг/м3. Размеры трубы d = 100 мм, h 1 = 4 м, h 2 = 0,5 м. Длина рычага а = 0,2 м, b =1 м. Собственным весом поршня пренебречь.
Рис. 2.21. Схема к задаче 2.7.5
Логично предположить, что сила F, необходимая для удержания поршня в равновесии, должна соответствовать избыточному давлению под ним, то есть весовому давлению столба жидкости:
Сила на штоке F ш, необходимая для его удержания в равновесии:
Сила F в соответствии с длинами плеч рычага равна:
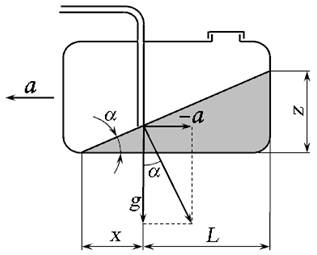
Задача 2.7.6. Автомобиль движется с ускорением а = 3,27 м/с2. Определить минимальное количество топлива в баке, обеспечивающее его подачу без подсоса воздуха. Считать, что бензопровод установлен на расстоянии L = 0,45 м от задней стенки бака, диаметр бензопровода мал по сравнению с длиной бака, высота h = 10 мм. Ширина бака b = 0,5 м, плотность бензина ρ = 750 кг/м3. Определить избыточное давление, оказываемое на заднюю стенку бензобака.
а) б) Рис. 2.22. Схема к задаче 2.7.6
Изобразим положение бензина в баке с минимальным объёмом (рис. 2.22, б). Обозначим стороны прямоугольного треугольника как (x + L) и z. Тогда:
Объём минимального количества бензина в баке, обеспечивающего его подачу без подсоса, будет равно:
Давление, оказываемое на заднюю стенку бензобака, определим по формуле (2.15):
Задача 2.7.7. На рисунке показана одна из возможных схем гидроусилителя сцепления автомобиля. Масло под давлением р 0 = 0,5 МПа подводится внутри вала и затем через отверстие - в полость между двумя совместно вращающимися цилиндром 1 и поршнем 2, который может скользить вдоль вала. Давление масла, увеличенное благодаря действию центробежных сил, заставляет поршень перемещаться вправо и обеспечивает этим силу нажатия, необходимую для выключения сцепления. Определить силу давления масла на поршень 2, если его диаметр D =120 мм, диаметр вала d = 20 мм, частота вращения n = 6000 об/мин, плотность масла ρ = 920 кг/м3.
Рис. 2.23. Схема к задаче 2.7.7
Определим угловую частоту вращения:
Увеличение давления за счет центробежной силы будет увеличиваться пропорционально увеличению расстояния от центральной оси элемента. В этом случае за увеличение давления примем его среднее значение в соответствии с формулой (2.13):
Давление в полости элемента с учётом увеличения давления за счёт действия центробежной силы будет равно:
Сила, с которой действует давление р на поршень, будет равна:
Задача 2.7.8. В сосуд диаметром d = 100 мм и высотой h 2 = 0,3 м залита жидкость до уровня h 1 = 0,2 м. Определить, до какой угловой скорости ω можно раскрутить сосуд, с тем, чтобы жидкость не выплеснулась из него.
Рис. 2.24. Схема к задаче 2.7.8
При ω = ωmax свободная поверхность жидкости займёт положение, изображённое на рис. 2.24. Уравнение свободной поверхности жидкости в виде поверхности параболоида имеет вид:
где z 0 - вертикальная координата вершины параболоида. Объём параболоида вращения W п согласно формуле (2.20) равен:
Выразим объём жидкости W ж, находящейся в сосуде объёмом W с, учитывая объём параболоида W п:
Поскольку можно вычислить объём жидкости W ж в сосуде, находящегося в состоянии покоя
Угловую скорость ω можно выразить из уравнения свободной поверхности жидкости в сосуде:
Задача 2.7.9. Резервуар заполнен жидкостью плотностью ρ = 870 кг/м3, высота столба жидкости h = 0,65 м. Основания трапеции боковой стенки а = 0,6 м, b = 0,35 м, длина х = 1,2 м. Определить усилие, действующее на каждый болт крепления боковых стенок и дна резервуара на глубине h, если количество болтов по длине х равно nх = 8 шт., по длине b равно nb = 3 шт. Определить диаметр болтов, если допустимое напряжение на разрыв стального болта
Рис. 2.25. Схема к задаче 2.7.9
Для решения задачи необходимо определить высоты центров тяжести hС и центров давления hD боковых стенок. Для наглядности графически отобразим положения центров тяжести и давления (рис. 2.25): - центр тяжести прямоугольной боковой стенки hС 1 = - центр давления прямоугольной боковой стенки hD 1 = - центр тяжести трапеции hC 2 = - центр давления трапеции hD 2 = Определим весовые давления, действующие в центре тяжести боковой стенки и трапеции: - давление р пр, действующее в центре тяжести прямоугольной боковой стенки
- давление, действующее в центре тяжести трапеции
Определим силы давления, действующие на боковые стенки. Для определения сил давления, действующих на боковые стенки, необходимо определить их площади: - площадь прямоугольной боковой стенки
где угол α определим как - площадь трапеции
Определим силы давления, действующие на боковую прямоугольную стенку и в форме трапеции: - на прямоугольную стенку
- на стенку в форме трапеции
Определим силы F, действующие на болты крепления боковых стенок и дна резервуара по линии b и х на глубине h со стороны жидкости. Эти силы будут равны по значению и противоположны по знаку силам реакции со стороны болтов крепления. Обозначим их как Fх (сила, действующая по длине х) и Fb (сила, действующая по длине b). Составим уравнение моментов относительно точки, расположенной на оси симметрии площадок (прямоугольной и трапеции) в верхней точке (точки А и Б). Уравнение моментов сил, действующих на прямоугольную стенку относительно точки А:
hD 1 =
Сила, действующая на каждый болт по длине х, будет равна:
Уравнение моментов сил, действующих на стенку в форме трапеции относительно точки Б:
Сила, действующая на каждый болт по длине b, будет равна:
Поскольку сила, действующая на каждый болт по длине х, несколько больше, чем по длине b, то диаметр болтов определим исходя из силы Fхn. Определим площадь сечения одного крепежного болта Sn из формулы:
Диаметр крепежного болта будет не менее dn = 2 мм. Задача 2.7.10. Горизонтальная металлическая цистерна круглого сечения диаметром d = 2 м и длиной L = 10 м полностью заполнена минеральным маслом (удельный вес масла 9∙103 Н/м3). Давление на поверхности масла равно атмосферному. Определить силу давления масла на внутреннюю криволинейную поверхность цистерны. Определить координаты центра тяжести тела давления.
Рис. 2.26. Схема к задаче 2.7.10
Определим плотность масла исходя из формул (1.3) и (1.4): ρ = Центр координат расположим в центре сечения цистерны, ось ОХ направим по горизонтали, ось ОZ - по вертикали по оси симметрии цистерны (рис. 2.26). Сила давления масла на внутреннюю криволинейную поверхность цистерны определим по формуле (2.19) как корень из суммы квадратов силы Px (сила давления масла на вертикальную проекцию оси ОZ цилиндрической поверхности цистерны) и силы Pz (сила тяжести тела давления, ограниченного осью ОZ и цилиндрической поверхностью), то есть:
Для определения силы Px по формуле необходимо определить площадь проекции цилиндрической поверхности Sz на ось ОZ и центр тяжести hC этой проекции для определения давления:
Сила Pz определим как половину веса масла:
Сила давления масла на внутреннюю криволинейную поверхность цистерны:
Определим координаты центра тяжести тела давления. Центр тяжести будет находиться на линии действия силы давления Px, то есть координата по оси ОZ будет равна
Координату х ц по оси ОХ определим, составив уравнение моментов относительно т. А:
Задача 2.7.11. Определить диаметр d р резервуаров - накопителей (ресиверов) 2 автоматической системы тормозов автомобиля, при котором будет обеспечиваться шесть торможений (n = 6) за счёт сжатого воздуха без включения компрессора 1. Последний включается и начинает нагнетать воздух в систему при избыточном давлении р 2 = 0,4 МПа и выключается при р 1 = 0,6 МПа. Кран управления 3 после каждого торможения выпускает воздух из тормозных цилиндров 4 в атмосферу. Принять: диаметр поршня тормозных камер d п = 180 мм, ходы поршней L п = 0,06 м, длины резервуаров L р = 0,8 м, атмосферное давление составляет 749,5 мм. рт. ст. Процесс расширения воздуха считать изотермическим. Объёмом трубопроводов пренебречь. Определить, сколько полных торможений без включения компрессора могут обеспечить эти резервуары, если автомобиль въехал на горный перевал (где атмосферное давление составляет 400 мм. рт. ст.) без использования тормозной системы.
Рис. 2.27. Схема к задаче 2.7.11
Изменение объёма газа связано с изменением его давления. Для решения задачи воспользуемся уравнением Бойля – Мариотта (1.7): р 1 где n – степенной показатель, равный при изотермическом процессе единице, то есть
Обозначим объём одного ресивера W 1, объём одной тормозной камеры 4 при одном рабочем ходе - W 2. Учитывая количество ресиверов и тормозных камер, а также количество торможений (n = 6), можно записать:
где После некоторых математических преобразований и сокращений получим:
Определим, сколько полных торможений может обеспечить тормозная система автомобиля на горном перевале. Для этого определим разность нормального и пониженного (на горном перевале) атмосферных давлений:
Эту разность давлений обозначим как дополнительное давление р доп, поскольку именно на эту разность повысится избыточное давление в ресиверах 2 из-за понижения атмосферного давления (р изб = р абс – р ат), так как абсолютное давление до въезда автомобиля на горный перевал и на нём при неработающем компрессоре будет одинаковым. Тогда избыточное давление в ресиверах р рес составит: р рес = р 1 + р доп = 600 000 + 46 588,35 = 646 588,35 Па. Запишем повторно:
p рес 3W1 = р 2(3W1 + 4nW2),
Количество полных торможений при въезде на горный перевал составит n = 7.
Гидродинамика Гидродинамика - это раздел гидравлики, в котором изучают законы движения жидкостей в зависимости от приложенных к ним сил. Движение жидкости может быть разделено на два основных вида - установившееся и неустановившееся. Движение жидкости называется установившимся, если каждая частица жидкости характеризуется определённой скоростью течения и давлением, неизменными во времени по величине и направлению. Неустановившимся называется такое движение, при котором скорость и давление в любой точке пространства, занятого жидкостью, изменяются с течением времени. В гидравлике потоком жидкости называют движущуюся массу жидкости, ограниченную твёрдыми поверхностями, поверхностями раздела жидкостей или свободными поверхностями. В зависимости от характера и сочетания ограничивающих поток поверхностей потоки делят на безнапорные, напорные и гидравлические струи. Безнапорные потоки ограничены сочетанием твёрдых поверхностей и свободной поверхностью жидкости, на которую действует атмосферное давление (например, поток в реке или канале, а также в трубе, работающей неполным сечением). Напорные потоки ограничены твёрдыми поверхностями, испытывающими давление со стороны жидкости, отличного от внешнего атмосферного давления (например, поток масла в трубопроводах гидросистем). Гидравлические струи ограничены только жидкостью или газовой средой (например, струя жидкости, истекающая в атмосферу из пожарного брандспойта).
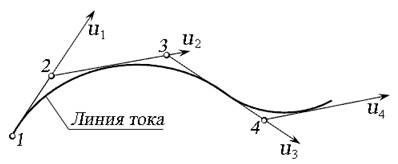
Рис. 3.1. Линия тока: u 1 … u 2 - векторы местных скоростей частиц жидкости в точках 1 … 4 в данный момент времени
Для создания математической модели поток жидкости рассматривают как совокупность элементарных струек, движущихся с различными скоростями. Каждая частица жидкости, обладающая элементарной массой, движется с определённой скоростью и за определённый промежуток времени пройдёт ряд точек пространства с различными скоростями (точки 1, 2, 3, рис. 3.1). В каждой точке частица имеет разную скорость (u 1 ≠ u 2 ≠ u 3). Действительная скорость, с которой движется частица жидкости в любой точке пространства, занятого жидкостью, называется местной скоростью. Кривая, проведённая внутри потока так, что векторы местных скоростей направлены по касательной к ней, называют линией тока. Линии тока, проведённые через все точки замкнутого элементарного контура, образуют трубку тока. Часть потока, заключённая внутри трубки тока, называют элементарной струйкой (рис. 3.2).
Рис. 3.2. Элементарная струйка
При установившемся движении: - элементарная струйка не меняет своей формы и ориентации в пространстве, трубку тока рассматривают как жёсткую трубку различного сечения с непроницаемыми стенками; - ввиду малости поперечного сечения струйки местные скорости во всех точках этого сечения считают одинаковыми, местные скорости изменяются при переходе от одного сечения струйки к другому. Местную скорость принимают за скорость элементарной струйки в данном сечении.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 2732; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.015 с.) |

 .
.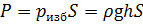 , (2.16)
, (2.16)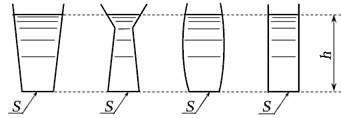
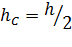 . Если свободная поверхность жидкости открыта в атмосферу (р 0 = р ат), то избыточное давление:
. Если свободная поверхность жидкости открыта в атмосферу (р 0 = р ат), то избыточное давление: .
. . (2.17)
. (2.17) , (2.18)
, (2.18)










 ; (2.19)
; (2.19) .
.
 и некоторой длиной (на схеме не показано). Сила Pх будет равна:
и некоторой длиной (на схеме не показано). Сила Pх будет равна: ,
, ,
, ,
, , а вертикальная составляющая Pz - через центр тяжести тела давления.
, а вертикальная составляющая Pz - через центр тяжести тела давления. - это высота столба жидкости в пъезометре (пъезометр – это стеклянная трубка, манометр жидкостного типа для измерения избыточного давления).
- это высота столба жидкости в пъезометре (пъезометр – это стеклянная трубка, манометр жидкостного типа для измерения избыточного давления). , (2.20)
, (2.20)
 ,
, .
. , откуда высота бензина в баке
, откуда высота бензина в баке = 1м.
= 1м. = 3,14 м3.
= 3,14 м3.
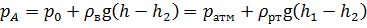 , откуда
, откуда
 =
= = 242310,5 Па = 0,24 МПа.
= 242310,5 Па = 0,24 МПа. , откуда
, откуда = 16,92 м.
= 16,92 м.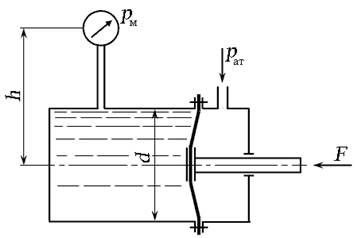
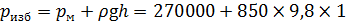 = 278330 Па.
= 278330 Па.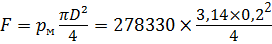 = 8740 Н = 8,74 кН.
= 8740 Н = 8,74 кН. = 98642 Па.
= 98642 Па.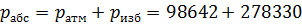 = 376972 Па = 0,377 МПа.
= 376972 Па = 0,377 МПа.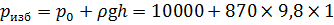 = 18526 Па.
= 18526 Па.
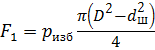 ,
, .
. = 79,87 Н.
= 79,87 Н.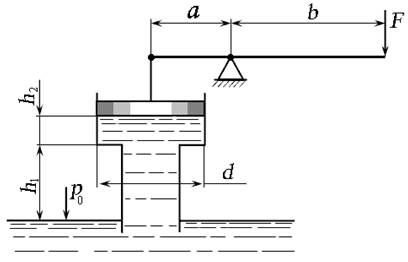
 = 44100 Па.
= 44100 Па. = 346,2 Н
= 346,2 Н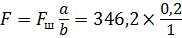 = 69,24 Н.
= 69,24 Н.
 = 0,33367, α = 18,45 град.
= 0,33367, α = 18,45 град. = 0,3 м,
= 0,3 м, = 0,25 м.
= 0,25 м. = 0,047 м3 = 47 л.
= 0,047 м3 = 47 л. = 2573,25 Па.
= 2573,25 Па.
 = 628 рад/с.
= 628 рад/с. = 635 кПа.
= 635 кПа.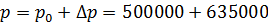 = 1135000 Па.
= 1135000 Па. =7945 Н.
=7945 Н.
 ,
, .
.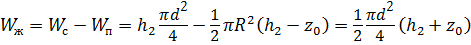 .
. , то можно записать:
, то можно записать: ,
, , откуда
, откуда = 0,1 м.
= 0,1 м. =
=  = 39,6 рад/с.
= 39,6 рад/с. = 7000 Н/см2.
= 7000 Н/см2.
 = 0,325 м;
= 0,325 м; = 0,43 м;
= 0,43 м;
 = 0,3 м;
= 0,3 м;
 = 0,4125 м.
= 0,4125 м. = 2771 Па;
= 2771 Па; = 2527,8 Па.
= 2527,8 Па. = 0,794 м2,
= 0,794 м2, = 5,2; α = 79,1 º;
= 5,2; α = 79,1 º; = 0,31 м2.
= 0,31 м2.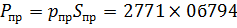 = 2198 Н;
= 2198 Н; = 783,6 Н.
= 783,6 Н.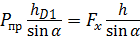 ,
, ,
, = 1465,3 Н.
= 1465,3 Н. = 183,2 Н.
= 183,2 Н. , откуда
, откуда = 497,3 Н.
= 497,3 Н. = 165,76 Н.
= 165,76 Н. , откуда
, откуда  = 0,0262 см2,
= 0,0262 см2, = 0,1826 см.
= 0,1826 см.
 =
=  = 918,37 кг/м3.
= 918,37 кг/м3. = 20 м2;
= 20 м2; = 1 м,
= 1 м, = 180 кН.
= 180 кН. = 141,3 кН.
= 141,3 кН. = 228835,5 Н.
= 228835,5 Н. .
. , откуда
, откуда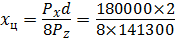 = 032 м.
= 032 м.
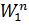 = p 2
= p 2 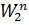 ,
, .
.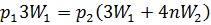 ,
,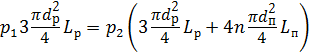 ,
, ,
, 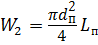 .
. , откуда
, откуда = 0,197 м ≈ 200 мм.
= 0,197 м ≈ 200 мм. = 46588,35 Па.
= 46588,35 Па.
 ,
, = 7,61.
= 7,61.