Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие сплошной среды .Нормальная жидкость.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Понятие сплошной среды.Нормальная жидкость. Сплошна́я среда́ — механическая система, обладающая бесконечным числом внутренних степеней свободы. Её движение в пространстве, в отличие от других механических систем, описывается не координатами и скоростями отдельных частиц, а скалярным полем плотности и векторным полем скоростей. В зависимости от задач, к этим полям могут добавляться поля других физических величин (концентрация, температура, поляризованность и др.) Если плотность сплошной среды постулируется равной константе, то такая сплошная среда называется несжимаемой. Жи́дкость — одно из агрегатных состояний вещества. Основным свойством жидкости, отличающим её от других агрегатных состояний, является способность неограниченно менять форму под действием касательных механических напряжений, даже сколь угодно малых, практически сохраняя при этом объёмЖидкое состояние обычно считают промежуточным между твёрдым телом и газом: газ не сохраняет ни объём, ни форму, а твёрдое тело сохраняет и то, и другое. Форма жидких тел может полностью или отчасти определяться тем, что их поверхность ведёт себя как упругая мембрана. Так, вода может собираться в капли. Но жидкость способна течь даже под своей неподвижной поверхностью, и это тоже означает несохранение формы (внутренних частей жидкого тела). Молекулы жидкости не имеют определённого положения, но в то же время им недоступна полная свобода перемещений. Между ними существует притяжение, достаточно сильное, чтобы удержать их на близком расстоянии. Вещество в жидком состоянии существует в определённом интервале температур, ниже которого переходит в твердое состояние (происходит кристаллизация либо превращение в твердотельное аморфное состояние — стекло), выше — в газообразное (происходит испарение). Границы этого интервала зависят от давления Как правило, вещество в жидком состоянии имеет только одну модификацию. (Наиболее важные исключения — это квантовые жидкости и жидкие кристаллы.) Поэтому в большинстве случаев жидкость является не только агрегатным состоянием, но и термодинамической фазой (жидкая фаза). Массовые и поверхностные силы Массовые силы это силы, пропорциональные массе жидкости. В случае однородной жидкости эти силы пропорциональны объёму. Прежде всего, к ним относится вес жидкости
где G – вес жидкости, V – объём жидкости, m – масса жидкости, g – ускорение свободного падения, Б – плотность жидкости, і – удельный вес жидкости. Как известно, масса является мерой инертности тела. Это свойство присуще и жидкостям, поэтому к массовым силам относятся и силы инерции:
где Fин – инерционная сила, v – скорость жидкости, t – время движения, a – ускорение движения. Силы инерции, действующие в жидкости, так же как и для твёрдого тела, могут проецироваться на оси. Поверхностные силы – силы, величины которых пропорциональны площади. К ним относят два вида сил. Силы поверхностного натяжения и силы вязкого трения. Последние проявляются только при движении жидкости и не играют никакой роли, когда жидкость находится в покое. Эти силы, как свойство вязкости, были рассмотрены при изучении свойств жидкостей. Уравнение Эйлера Рассмотрим движение идеальной жидкости. Выделим внутри неё некоторый объём V. Согласно второму закону Ньютона, ускорение центра масс этого объёма пропорционально полной силе, действующей на него. В случае идеальной жидкости эта сила сводится к давлению окружающей объём жидкости и, возможно, воздействию внешних силовых полей. Предположим, что это поле представляет собой силы инерции или гравитации, так что эта сила пропорциональна напряжённости поля и массе элемента объёма. Тогда
где S — поверхность выделенного объёма, g — напряжённость поля. Переходя, согласно формуле Гаусса — Остроградского, от поверхностного интеграла к объёмному и учитывая, что
В силу произвольности объёма V подынтегральные функции должны быть равны в любой точке:
Выражая полную производную через конвективную производную и частную производную:
получаем уравнение Эйлера для движения идеальной жидкости в поле тяжести:
Для идеальной Поток идеальной жидкости, как указывалось ранее, можно представить совокупностью элементарных струек жидкости. Скорости по сечению потока неодинаковы, причём в середине потока скорости наибольшие, а к периферии они уменьшаются (струйная модель потока). Это означает, что различные струйки в одном сечении имеют различные значения кинетической энергии. Отсюда следует, что кинетическая энергия, посчитанная с использованием скоростей элементарных струек uS, и кинетическая энергия, посчитанная с использованием значения средней скорости потока V, будет иметь разные значения. Выясним, какова эта разница. Кинетическая энергия элементарной струйки
где
Проинтегрировав выражение для Для вязкой Перед тем, как записать уравнение Бернулли для потока вязкой жидкости необходимо оговорить два момента. Поток жидкости отличается от элементарной струйки тем, что он имеет реальные размеры поперечного сечения, которые могут быть довольно значительных размеров. Распределение давлений и скоростей по сечению потока может быть неравномерным. Рассмотрим распределение давления. В плоскости перпендикулярной направлению движения, гидродинамическое давление распределяется по закону гидростатики. В связи с этим справедливо условие:
т.е. сумма отметки z и пьезометрической высоты В связи с тем, что распределение местных скоростей U в плоскости сечения потока неравномерно и в большинстве случаев неизвестно, то возникают трудности с определением кинетической энергии потока, т.е. с третьим слагаемым в уравнении Бернулли Для наиболее распространенных случаев движения жидкости значения ± следующее: при ламинарном движении в круглой трубе ± = 2, при турбулентном – зависит от режима и принимает значение ± = 1,1 Коэффициент Кориолиса Коэффициент Кориолиса представляет собой отношение действительной кинетической энергии к кинетической энергии потока, вычисленной по средней скорости. Таким образом, поправочный коэффициент учитывает неравномерность скорости по живому сечению потока. Графики Никурадзе и Мурина Наиболее полные исследования по определению зависимости коэффициента l от числа Рейнольдса и от относительной шероховатости были выполнены И. Никурадзе. И. Никурадзе испытал ряд труб с искусственно созданной шероховатостью на их внутренней поверхности. Шероховатость была получена путем приклейки песчинок определенного размера, полученных просеиванием через сита. Такая шероховатость называется равномерно зернистой. Испытания были проведены при широком диапазоне относительных шероховатостей Данные опытов И. Никурадзе изобразил на графике, где по оси абсцисс откладывались логарифмы величин Re, а по оси ординат – логарифмы 100 l при различных значениях относительных шероховатостей (рис. 6.6).
Рис. 6.6. График Никурадзе
При Re < 2300 (lg Re < 3,36) – прямая 1 – имеет место ламинарный режим и l зависит только от числа Рейнольдса и не зависит от шероховатости стенок. При Последняя область 5 представлена линиями, параллельными оси абсцисс, что свидетельствует о том, что здесь коэффициент гидравлического трения зависит только от шероховатости. Эту область обычно называют областью квадратичного сопротивления, так как потери напора по длине пропорциональны квадрату скорости. Для труб с естественной шероховатостью закон изменения l от Re получается несколько иным, без подъема кривых после отклонения их от линии гладких труб. Различие объясняется тем, что в трубах с естественной шероховатостью выступы шероховатости имеют различную высоту и при увеличении числа Рейнольдса начинают выступать за пределы ламинарного слоя не одновременно, а при разных Re. Поэтому переход от линии «гладких» труб к горизонтальным прямым, соответствующим квадратичному закону, происходит более плавно, без провала кривых, что наглядно представлено на графике Г. А. Мурина (рис. 6.7).
Рис. 6.7. График Мурина
Длинные трубопроводы Это трубопроводы постоянного по длине диаметра, у которых основными являются потери напора по длине, а местными потерями напора и скоростным напором можно пренебречь. Потери напора по длине трубопровода определяют по формуле Дарси—Вейсбаха:
Учитывая, что расход Q = VЧS и скорость движения потока
где А — удельное сопротивление трубопровода, определяемое по справочным таблицам; Для переходной области удельное сопротивление Ао=А*b, где b — поправочный коэффициент, учитывающий зависимость коэффициента гидравлического трения l от числа Рейнольдса. Кроме удельного сопротивления А в литературе по гидравлике для решения задач приводится способ расчета длинных трубопроводов, базирующийся на формуле Шези.
Широко применяемые гидравлические параметры — это модуль расхода
Короткие трубопроводы рассчитывают непосредственно по уравнению Бернулли с учетом потерь по длине и местных сопротивлений
Истечения через отверстия. Малое отверстие– отверстие диаметр, которого меньше 0,1 напора над этим отверстием.
Тонкой стенкой называется стенка, толщина которой меньше 0,5 диаметра и имеющая открытый острый край. В этом случае жидкость испытывает только местные сопротивления. При подходе жидкости к отверстию траектории ее частиц не параллельны. За счет прямолинейности движения давление в струе жидкости возрастает от кромок к центру, а скорость уменьшается. В результате чего струя сжимается. На расстоянии равном половине диаметра движение жидкости становится параллельным струйным, а такое сечение называется сжатым. Коэффициент сжатия (?) – отношение площади сжатой струи к площади отверстия. Рассмотрим истечение жидкости через малое отверстие с тонкой стенкой при постоянном напоре в атмосферу. Для этого запишем уравненеи Бернулли для двух сечений (1-на поверхности воды в резервуаре, 2 — в сжатом сечении) Плоскость отчета проходит через центр тяжести отверстия. z1 + z1 = H; z2 = 0 P1 = P2 = Pa ?1 = 0;?2 =?c H + ?c = где Коэффициент скорости– это отношение реальной скорости в сжатом сечении к теоретической (максимально возможной) скорости. Q =?c Sc? = Q =?c?S0 =?S0 ? =?? — коэффициент расхода Q =? S0
Опытными исследованиями были получены средние коэффициенты при истечении в атмосферу: Коэффициент скорости? = 0,97 Коэффициент сжатия?= 0,64 Коэффициент расхода? = 0.62 Коэффициенты истечения Коэффициенты истечения зависят от числа Рейнольдса Re, особенно при малых его значениях, однако при Re больше 105 влияние сил вязкостного трения на коэффициенты истечения пренебрежимо мало и можно считать их практически постоянными. Число Рейнольдса вычисляют по формуле
где Средние значения коэффициентов истечения В случаях, когда число Re меньше 105, коэффициенты истечения находят из графика А.Д. Альтшуля (рис. 5.1), составленного на основании опытов разных авторов. Из графика следует, что с увеличением числа Re коэффициент расхода
Рисунок 5.1 – График А.Д. Альтшуля Насадки и их виды Движения в открытых руслах Понятие сплошной среды.Нормальная жидкость.
Сплошна́я среда́ — механическая система, обладающая бесконечным числом внутренних степеней свободы. Её движение в пространстве, в отличие от других механических систем, описывается не координатами и скоростями отдельных частиц, а скалярным полем плотности и векторным полем скоростей. В зависимости от задач, к этим полям могут добавляться поля других физических величин (концентрация, температура, поляризованность и др.) Если плотность сплошной среды постулируется равной константе, то такая сплошная среда называется несжимаемой. Жи́дкость — одно из агрегатных состояний вещества. Основным свойством жидкости, отличающим её от других агрегатных состояний, является способность неограниченно менять форму под действием касательных механических напряжений, даже сколь угодно малых, практически сохраняя при этом объёмЖидкое состояние обычно считают промежуточным между твёрдым телом и газом: газ не сохраняет ни объём, ни форму, а твёрдое тело сохраняет и то, и другое. Форма жидких тел может полностью или отчасти определяться тем, что их поверхность ведёт себя как упругая мембрана. Так, вода может собираться в капли. Но жидкость способна течь даже под своей неподвижной поверхностью, и это тоже означает несохранение формы (внутренних частей жидкого тела). Молекулы жидкости не имеют определённого положения, но в то же время им недоступна полная свобода перемещений. Между ними существует притяжение, достаточно сильное, чтобы удержать их на близком расстоянии. Вещество в жидком состоянии существует в определённом интервале температур, ниже которого переходит в твердое состояние (происходит кристаллизация либо превращение в твердотельное аморфное состояние — стекло), выше — в газообразное (происходит испарение). Границы этого интервала зависят от давления Как правило, вещество в жидком состоянии имеет только одну модификацию. (Наиболее важные исключения — это квантовые жидкости и жидкие кристаллы.) Поэтому в большинстве случаев жидкость является не только агрегатным состоянием, но и термодинамической фазой (жидкая фаза).
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 691; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.116.245 (0.011 с.) |

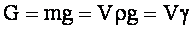 ,
,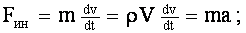
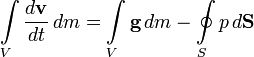 ,
,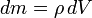 , где
, где  — плотность жидкости в данной точке, получим:
— плотность жидкости в данной точке, получим: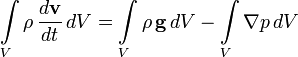
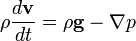


 равна:
равна:

 - масса жидкости плотностью
- масса жидкости плотностью  , протекающей через живое сечение элементарной струйки
, протекающей через живое сечение элементарной струйки  со скоростью
со скоростью  за время dt, равная:
за время dt, равная: .
. , получим выражение для кинетической энергии потока идеальной жидкости
, получим выражение для кинетической энергии потока идеальной жидкости  .
.
 во всех точках сечения потока остается одинаковой, хотя меняется для различных сечений.
во всех точках сечения потока остается одинаковой, хотя меняется для различных сечений. . Поэтому вводим корректирующий коэффициент ±, представляющий собой отношение действительной кинетической энергии потока к кинетической энергии, подсчитанной по средней скорости в сечении. Корректив ± называется коэффициентом кинетической энергии потока или коэффициентом Кориолиса, и отражает неравномерность распределения местных скоростей по сечению потока.
. Поэтому вводим корректирующий коэффициент ±, представляющий собой отношение действительной кинетической энергии потока к кинетической энергии, подсчитанной по средней скорости в сечении. Корректив ± называется коэффициентом кинетической энергии потока или коэффициентом Кориолиса, и отражает неравномерность распределения местных скоростей по сечению потока. 1,3. Обычно ± определяют опытным путем.
1,3. Обычно ± определяют опытным путем.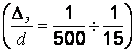 , а также чисел Рейнольдса
, а также чисел Рейнольдса  .
.

 – участок 2 – наблюдается быстрый переход от ламинарного режима к турбулентному. Далее начинается прямая 3, характеризующая зависимость l от числа Рейнольдса для гидравлически «гладких» труб, у которых величина выступов шероховатостей меньше толщины ламинарной пристенной пленки. Далее кривые зависимости l от Re расходятся. Участки кривых 4 характеризуют собой переход от гидравлически «гладких» труб к гидравлически «шероховатым» трубам 5, т. е. в зоне 4 – 5 коэффициент гидравлического трения l зависит как от шероховатости, так и от Re.
– участок 2 – наблюдается быстрый переход от ламинарного режима к турбулентному. Далее начинается прямая 3, характеризующая зависимость l от числа Рейнольдса для гидравлически «гладких» труб, у которых величина выступов шероховатостей меньше толщины ламинарной пристенной пленки. Далее кривые зависимости l от Re расходятся. Участки кривых 4 характеризуют собой переход от гидравлически «гладких» труб к гидравлически «шероховатым» трубам 5, т. е. в зоне 4 – 5 коэффициент гидравлического трения l зависит как от шероховатости, так и от Re.

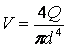 тогда
тогда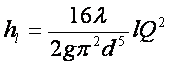 или
или 

 , сопротивление трубопровода ST=A*l, проводимость трубопровода
, сопротивление трубопровода ST=A*l, проводимость трубопровода  . С помощью вышеуказанных параметров потери напора по длине можно определить следующим образом:
. С помощью вышеуказанных параметров потери напора по длине можно определить следующим образом:

 +
+  = z2 +
= z2 +  +
+  + h1-2
+ h1-2 +
+  = 0+
= 0+  +
+ 
 =
= 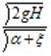 =
= 
 =
=  — коэффициент скорости, постоянная.
— коэффициент скорости, постоянная.

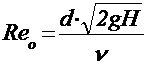 ;
;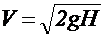 – скорость истечения идеальной жидкости.
– скорость истечения идеальной жидкости.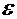 ,
, 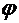 ,
, 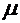 ,
, 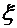 для малых отверстий в тонкой стенке и разных насадков при числах Re больше 105 приведены справочных материалах.
для малых отверстий в тонкой стенке и разных насадков при числах Re больше 105 приведены справочных материалах.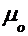 сначала увеличивается, а затем, достигнув максимального значения (
сначала увеличивается, а затем, достигнув максимального значения (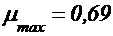 при Re=350), уменьшается и стабилизируется на значении, близком к
при Re=350), уменьшается и стабилизируется на значении, близком к 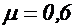 . Таким образом, коэффициенты истечения при достаточно больших числах Re зависят только от формы отверстий и насадков.
. Таким образом, коэффициенты истечения при достаточно больших числах Re зависят только от формы отверстий и насадков.