Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Истечение через большое отверстиеСодержание книги Поиск на нашем сайте
Отверстие считают малым, когда его вертикальные размеры d < 0,1Н. Большим отверстием будем считать такое отверстие, для которого тот же d> 0,1Н. Рассматривая истечение через малое отверстие, практически пренебрегли различием скоростей в разных точках сечения струи. В этом случае поступить так же мы не сможем. Задача та же: определить расход и скорости в сжатом сечении. Поэтому расход определяют следующим способом: выделяют бесконечно малую горизонтальную высоту dz. Таким образом, получается горизонтальная полоса с переменной длиной bz. Тогда, интегрировав по длине, можно найти элементарный расход
где Z – переменный напор по высоте отверстия, на такую глубину погружен верх выбранной полосы; ? – коэффициент расхода через отверстие; bz – переменная длина (или ширина) полосы. Расход Q (1) можем определить, если? = const и известна формула bz= f(z). В общем случае, расход определяют по формуле
Если форма отверстия прямоугольная, то bz= b = const, интегрировав (2), получаем:
где Н1, Н2 – напоры на уровнях соответственно у верхней и у нижней кромок отверстия; Нц – напор над центром отверстия; d – высота прямоугольника. Формула (3) имеет более упрощенный вид:
В случае истечения через круглое отверстие пределами интегрирования в (2) служат Н1= Нц – r; Н2 = Нц + r; Z = Нц – rcos?; dz =?sin?d?; bz = 2r?sin?. Избегая математического излишества, приведем конечную формулу:
Как видно из сравнений формул, особой разницы в формулах для расхода нет, только при больших и малых отверстиях коэффициенты расхода разные Коэффициенты истечения Коэффициенты истечения зависят от числа Рейнольдса Re, особенно при малых его значениях, однако при Re больше 105 влияние сил вязкостного трения на коэффициенты истечения пренебрежимо мало и можно считать их практически постоянными. Число Рейнольдса вычисляют по формуле
где Средние значения коэффициентов истечения В случаях, когда число Re меньше 105, коэффициенты истечения находят из графика А.Д. Альтшуля (рис. 5.1), составленного на основании опытов разных авторов. Из графика следует, что с увеличением числа Re коэффициент расхода
Рисунок 5.1 – График А.Д. Альтшуля Насадки и их виды Движения в открытых руслах Условия равномерного движения в открытом русле Равномерное движение жидкости характеризуется прямыми параллельными линиями токов (траекториями), а также постоянством местной осредненной во времени скорости вдоль каждой линии тока. Следовательно, для существования равномерного движения необходимо выполнение ряда условий. На свободной поверхности безнапорных потоков устанавливается постоянное, как правило, атмосферное давление. Поэтому пьезометрический уклон Iр для таких потоков соответствует уклону свободной поверхности I c, т. е. Iр = I c. Ранее было установлено, что для равномерных потоков пьезометрический уклон равняется гидравлическому, т. е. Iр = I. Значит, равномерное безнапорное движение возможно при соблюдении равенства Iр = I = I c. Для этого (рис. 7.2) необходимо, чтобы величина скоростного напора по длине потока также оставалась бы постоянной. Этим диктуется соблюдение следующих условий: · русло – призматическое; · расход воды постоянен (Q = const); · глубина h, а следовательно, форма и площадь живого сечения ω и χ, R постоянны; · линия дна не имеет перелома, т. е. i = sin α= const, при этом i >0; · шероховатость дна и стенок русла постоянна по длине (п = const); · местные сопротивления в русле отсутствуют. Полностью удовлетворить всем условиям возможно только в искусственных руслах. Основное уравнение безнапорного равномерного движения
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.55.14 (0.005 с.) |

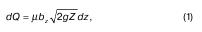
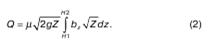
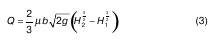
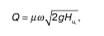

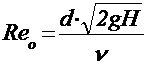 ;
;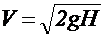 – скорость истечения идеальной жидкости.
– скорость истечения идеальной жидкости.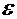 ,
, 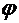 ,
, 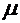 ,
, 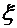 для малых отверстий в тонкой стенке и разных насадков при числах Re больше 105 приведены справочных материалах.
для малых отверстий в тонкой стенке и разных насадков при числах Re больше 105 приведены справочных материалах.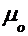 сначала увеличивается, а затем, достигнув максимального значения (
сначала увеличивается, а затем, достигнув максимального значения (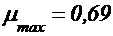 при Re=350), уменьшается и стабилизируется на значении, близком к
при Re=350), уменьшается и стабилизируется на значении, близком к 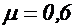 . Таким образом, коэффициенты истечения при достаточно больших числах Re зависят только от формы отверстий и насадков.
. Таким образом, коэффициенты истечения при достаточно больших числах Re зависят только от формы отверстий и насадков.