
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Введение в механику сплошной средыСодержание книги
Поиск на нашем сайте
Введение в механику сплошной среды Механика сплошной среды (МСС) – наука о движении газообразных, жидких и твердых деформируемых тел. Основой МСС являются подходы и методы, развитые теоретической механикой, которая рассматривает движения материальной точки, дискретных систем материальных точек и абсолютно твердого тела с изменяющимися расстояниями между ними во время движения. Как и теоретическая механика, МСС инструментом исследования физических тел использует модели процессов или явлений. В ряде случает, например, при движении газов, процессы, проистекающие в деформируемых средах, тесно связаны с термодинамическими явлениями в этих средах. Поэтому в основе МСС лежат как законы теоретической механики, так и законы термодинамики. МСС является теоретической базой для таких дисциплин как гидромеханика ньютоновских и неньютоновских жидкостей, газовая динамика, подземная гидромеханика, теория упругости, теория пластичности. Основные положения Гипотеза сплошности Явления, рассматриваемые в МСС, носят макроскопический характер. Это позволяет не рассматривать молекулярное строение вещества, а рассматривать физические тела как сплошные среды. Газ, жидкость, твердое деформированное тело рассматривают как среду непрерывным образом заполняющая часть пространства, т.е. представляющая собой непрерывный континуум, состоящий из множества дискретных материальных точек. С физической точки зрения принятие модели сплошности означает, что при макроскопическом описании всякий «бесконечно малый объем» содержит достаточно большое число молекул. Например, кубик воздуха с ребром 10-3 мм содержит 2*106 молекул. Отсюда видено, что предлагаемая идеализация не будет применимой лишь при очень больших разряжения. Газ и жидкость называют жидкостью, только газ – сжимаемая, а капельная жидкость –несжимаемая жидкость. Области и разделы МСС МСС возникла в связи с решением таких задач, как установление закономерностей при истечении жидкостей из сосудов, просачивание жидкости через грунт, прогиба балок, находящихся под нагрузкой и т.д. С помощью и на основе методов и данных, развитых в теоретической механике, в МСС рассматриваются движение тел с изменяющимися расстояниями между точками этих тел во время движения. В настоящее время МСС (механику сплошной среды) разделяют на две крупные области МЖГ (механику жидкости и газа), которая именуется гидромеханикой, и МДТ механику твердо деформированного тела. Гидромеханика включает в себя следующие разделы: 1) механика идеальной жидкости; 2) механика вязкой жидкости (или ньютоновской жидкости); 3) механика невязкой жидкости (или неньютоновской жидкости); 4) механика турбулентных течений. К гидромеханике примыкают механика фильтрационных течений и ряд других разделов механики. Механика деформированных тел состоит из: 1) теория упругости; 2) теория пластичности; 3) теория ползучести;4) механика сыпучих тел. К МДТ примыкают теория прочности и механика разрушения. Такое разделение МСС связано с тем, что различные тела даже при одних и тех же условиях ведут себя по-разному. Поэтому определяющие параметры и функции, граничные условия и дифференциальные уравнения так же не одинаковы. Основные задачи механики сплошных сред в бурении Основной задачей механики сплошных сред в бурении – снижение затрат времени и средств при строительстве и эксплуатации скважин, предупреждение и ликвидация аварий. Примерами могут служить задачи связанные с: разрушением горных пород; транспортировкой вырубленной породы на поверхность; определением гидравлических потерь в скважине; интенсивностью поглощения бурового раствора; оценка устойчивости и прочности стенок скважин; и др. Инструментарий МСС Методы достижения поставленной задачи основываются на фундаментальных законах ньютоновской механики (сохранения массы, количества движения, энергий), законах термодинамики, уравнений состояния, и большой совокупности экспериментальных данных. 2. среды, применяемые и встречающиеся при бурении нефтяных и газовых скважин [2]
С позиции МСС буровой и цементный растворы, горные породы и содержащиеся в них флюиды, материал, из которого изготавливается бурильные и обсадные трубы – сплошные среды. Основы течения сред Жидкость, движущаяся в трубе, всегда имеет неподвижный слой у стенки Рис.1. Здесь Как можно видеть, скорость потока на поверхности стенки равна нулю и постепенно увеличивается до максимального значения. Это результат скольжения одного слоя по другому. Таким образом, поток жидкости – это результат действия скольжения, поэтому для существования движения необходим приток энергии, например, в виде насоса. Скольжение слоев жидкости сопровождается напряжениями сдвига, которые зависят от скорости и вязкости жидкости. Вязкость Вязкость – свойство, определяющее величину напряжений сдвига, возникших при скольжении одного слоя по другому. Вязкость – мера сил внутреннего сопротивления, определяемых силами сцепления молекул жидкости при их вынужденном движении. Вязкость зависит от типа и температуры жидкости. Как известно с повышением температуры вязкость жидкости изменяется. В газах повышение температуры вызывает увеличение амплитуду колебаний молекул и уменьшает силы сцепления. Это приводит к повышению вязкости с повышением температуры. Для буровых растворов вязкость определяется количеством и размером твердых частиц в жидкости. Вязкость жидкостей связана с изменением параметров деформации элементарного объема (кубика) жидкости Рис. 2. На кубик действует сила F, приложенная параллельно поверхности поперечного сечения А. Напряжение сдвига t определится как:
Это напряжение вызывает деформацию кубика жидкости (Рис. 2а) и последний принимает ромбическую форму (Рис.2б). Деформация сдвига рассматривается как скорость сдвига и описывается отношением разности скоростей вверху Скорость изменения сдвига g определится как:
Рассмотрим типы жидкостей, модели которых используются при расчете процессов связанных с бурением нефтяных и газовых скважин. Типы жидкостей Ньютоновская жидкость Жидкости, характеризующиеся линейной зависимостью между t и g называется ньютоновской. В жидкостях данного типа вязкость зависит только от температуры. Примерами являются вода, нефть. Зависимость напряжением сдвига t от скорости сдвига g для ньютоновской жидкости приведена на Рис. 3. Коэффициент пропорциональности между напряжением сдвига t и скоростью изменения сдвига g - вязкость (динамическая) жидкости m:
или с учетом уравнения (2.1) и (2.2):
Знак минус показывает, сто скорость от центра к стенке уменьшается при увеличении расстояния Неньютоновская жидкость В неньютоновской жидкости зависимость между напряжением сдвига t и скоростью изменения сдвига g нелинейная. Примерами могут быть буровой и цементные растворы. Рассмотрим три основных типа неньютоновской жидкости. Типы буровых растворов Буровой раствор можно определить как суспензию твердой фазы и жидкой. Обычно используют буровые растворы на: водной; нефтяной: эмульсионной основе. Буровые растворы на водной основе - Чистая вода. Применяются для бурения пластов с почти нормальным давлением, саженных крепкими компактными пародами; - Естественный буровой раствор. Смесь воды с глинами и сланцами, получаемая в процессе прокачки воды через скважину. Характеризуется высокой водоотдачей и позволяет получать толстую глинистую корку. - Кальциевые буровые растворы. Основное преимущество обусловливается способностью содержать высокую концентрацию вырубленной породы без изменения вязкости. - Лигносульфонатные буровые растворы. Применяют в случаях: когда требуются буровые растворы высокой плотности (1680 кг/м3); работа с умеренно высокими температурами (121- 149 ºС); при высокой концентрации вырубленной пароды (поваренной соли, гипса); если необходима низкая водоотдача. Основной недостаток – блокировка пор продуктивной зоны. - Хлор калиевые полимерные растворы. Используются для бурения потенциально продуктивных песков (углеводородных зон), где пресная вода отрицательно влияет на проницаемость. Вследствие низкого содержания твердой фазы такие растворы часто называют недиспергированными. - Растворы, насыщенные солью. Применяют для разбуривания соленых куполов и интервалов, так как он препятствует расширению ствола скважины. Прочность геля Прочность геля – это мера способности бурового раствора образовывать и сохранять загущенную структуру. Она аналогична сопротивлению сдвига и определяет способность бурового раствора удерживать твердые частицы во взвешенном состоянии. Прочность геля также определяет тиксотропные свойства раствора и, следовательно, вязкость неподвижного бурового раствора. Тиксотропия обозначает свойство суспензии флюида типа бурового раствора, образовывать непрочную структуру в состоянии покоя и принимать жидкое состояние во время движения. Прочность геля бурового раствора можно определить по вискозиметру. Пробу бурового раствора встряхивают с большой скоростью и затем оставляют в покое на время от 10 с до 10 мин. В качестве значения прочности геля обычно берется показания вращающегося момента равного 3 об/мин. Прочность геля измеряется в Па. Дополнительным оценочным параметром бурового раствора может служить водородный показатель рН. рН является важным индикатором для борьбы с коррозией. рН показатель определяют как отрицательный логарифм содержания ионов водорода (H+) в растворе т.е. рН=-lg(H+). Установлено, что зависимость между концентрациями (H+) и (ОH-) для большинства растворов постоянно и определяется как: (H+)·(ОH-)=10-14. Для предупреждение коррозии обсадных труб и т.д., необходимо поддерживать минимальное значение рН =7, которое достигается при равной концентрации в электролитическом растворе катионов водорода (H+) и гидроксильных групп (ОH-). (H+)=(ОH-)=10-7. В таблице приведены классификация растворов по рН показателю.
Кинематика сплошной среды Общая задача кинематики – описание движения среды. Так как сплошная среда представляет собой непрерывную совокупность точек, то описание движения среды - значит, описать движение всех ее точек. Существует два исторически сложившихся способа задания движения – Лагранжа и Эйлера. Способ Лагранжа заключается в задании кинематических уравнений движения в виде совокупности переменных Лагранжа (xi, t):
Здесь, текущее координата xi определяется координатами фиксированной точки среды xi и временем t. Основная задача МСС – определение закона движения (2.1). Задание движения проекции скоростей и ускорений точек среды на оси координат определяются как:
Способ Эйлера заключается в задании переменных скорости и ускорения как функции переменных Эйлера - координат точек пространства xi и времени t:
Основное различие между методами Лагранжа и Эйлера состоит в том, что с точки зрения Лагранжа нас интересуют законы изменения положения, скорости, ускорения и других величин данной индивидуальной точки сплошной среды, а с точки зрения Эйлера – перемещение, скорость, ускорение и т.д. в точке пространства, мимо которой в данный момент проходит частица. В настоящее время наиболее применяемым способом является способ Эйлера. Запись уравнения движения среды в переменных Эйлера позволяет записать изменения расчетной (искомой) функции в виде:
Здесь Течение в щелевом канале Ламинарное течение ньютоновской жидкости основными характеристиками потока в щели являются: - объемный расход - средняя скорость - коэффициент сопротивления Здесь 2h – ширина щели; b – глубина щели; L – высота щели; Например, при
Ламинарное течение неньютоновской жидкости (Бингама) Схема профиля скорости в щелевом канале неньютоновской жидкости (Бингама) приведена на Рис. 8. Для неньютоновской жидкости Шведова-Бингама условие страгивания покоящейся жидкости является соотношение:
здесь Условием существования движения является соотношение:
здесь Для практических инженерных расчетов представляет интерес случаи, когда - объемный расход - средняя скорость - коэффициент сопротивления из уравнений (4.6, 4.7) можно выразить перепад давлений:
Здесь
Например, при
Элементы теории деформаций Характерной чертой движения сплошной среды является ее деформация т.е. изменение расстояния между отдельными точками среды. Как известно из теоретической механики деформация элементарного объема среды в окрестности рассматриваемой точки полностью определяется шестью величинами Связь компонентов тензоров деформации
Если известны компоненты деформации
Остальные уравнения получаются круговой заменой индексов (1-2-3-1). Таким образом, условие совместимости (5.2) является уравнениями, которые связывают компоненты тензора деформации В любой точке тела всегда существует, по крайней мере, одна тройная взаимно перпендикулярных направлений, таких, что деформация элемента в окрестности точки определяется только удлинением (укорочением)
где Характеристикой искажения формы элемента сплошной среды служит инвариантная величина, называемая интенсивностью деформации сдвига:
Здесь Классификация горных пород По полученной деформационной кривой находят основные механические параметры тела, устанавливают меру пластичности. Возможные виды деформационных кривых и соответствующие им формы разрушений для горных пород приведены на Рис 17. 1 – очень хрупкая, деформация до внезапного разрыва, характеризуемого образование трещин отрыва перпендикулярно к наименьшему главному напряжению. Накопленная при этом деформация не превышает 1%; 2 – хрупкая, наблюдается малая пластическая деформация до разрыва и образуются трещины отрыва и скола. Накопленная при этом деформация не превышает 1-5%; 3 – умеренно хрупкая, поведение промежуточное между хрупким и текучим, пик обозначает нарушение целостности без общей потере связности. Разрушение происходит в результате образования трещин скола. Накопленная при этом деформация не превышает 2-8%; 4 – умерено пластическая. Разрушение сопровождается рассеянной деформацией. Накопленная при этом деформация не превышает 5-10; 5 – идеально пластическая, хорошо выражен предел текучести, сменяющийся однородным течением. Деформация до разрыва более 10%; 6 – пластическая с упрочнением, предел текучести слабо выражен, процесс сопровождается работой упрочнения. Деформация до разрыва более 10%. Принадлежность горной пароды к одному из приведенных типов определяет расчетную математическую модель и предельное состояние. Критерии прочности Условие перехода какого-либо элемента нагруженного твердого тела в состояние хрупкого разрушения или пластического течения – критерий прочности при кратковременном нагружении. При одноосном напряженном состоянии критерий прочности оценивается предельным значением напряжения (см. выше 5.14); При переходе к сложному состоянию критерий прочности в общем случае определяется некоторой поверхностью:
Здесь В инженерных расчетах применяют выражения вида:
Здесь вид функции правой части определяют экспериментально для конкретных материалов. В частности при
При изучении анизотропии горных пород чаще всего ограничиваются изучением свойств пород в плоскости, параллельной напластованию, и плоскости, перпендикулярной к напластованию, считая любое из направлений в этих плоскостях эквивалентными в отношении механических свойств. Такие тела принято называть транверсально-изотропными. Рассмотрим упругие постоянные некоторых горных пород, заимствованы из разных литературных источников Рис. 18. Здесь Для большинства горных пород модули сдвига рекомендуется вычислять по формулам:
где Так как прочность горных пород на сжатие существенно отличается от прочности на растяжение или сдвиг, как по значению, так и по направлению, то в случае, когда необходимо учесть воздействия происходящих в направлениях, отличающихся от направлений плоскостей напластования (параллельных и перпендикулярных) применяется обобщенные критерии анизотропных тел. К таким критериям можно отнести обобщения критерия Мора по главным направлениям:
Буквенные обозначения являются коэффициентами, характеризующие отношения между критериями прочности на растяжения и сжатие плоскости напластования и перпендикулярной к ней. Литература 1. Рабинович Н.Р. Инженерные задачи механики сплошной среды в бурении. –М.: Недра, 1989. – 270 с. 2. Рабира. Х. Технология бурения нефтяных скважин. /Под. ред. В.Г. Григулецкого. - М.: Недра, 1989. - 413 с. 3. Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. Нефтегазовая гидромеханика. Учебник для вузов. – М.-Ижевск: - Институт компьютерных исследований, 2005. – 544 с. Дополнительная литература 1. Справочник по гидравлике /Под. ред. В.А. Большакова. – Киев, Вища школа, 1977. – 280 с. 2. Кутателадзе С.С, основы теории теплообмена. – Новосибирск: Наука, 1970. – 658 с. 3. Геологические основы разработки нефтяных месторождений. – М.: Недра, 1975. – 534 с.7. Гиматудинов Ш.К. Физика нефтяного и газового пласта. – М.: Недра, 1971. – 309 с. 4. Амикс Д., Басе Д., Уайтинг Р, Физика нефтяного пласта. – М.: Гостоптехизтат, 1962. – 572 с. 5. Данилов В.Л., Кац Р. М. Гидродинамические расчеты взаимного вытеснения жидкостей в пористой среде. – М.: Недра, 1980. – 264 с. 6. Сидоров Н.А. Бурение и эксплуатация нефтяных и газовых скважин. учебник для техникумов. – М.: Недра, 1982, - 376 с. Темы рефератов (дополнительные темы для изучения)
Напряженное и деформированное состояние системы “скважина-пласт” Введение в механику сплошной среды Механика сплошной среды (МСС) – наука о движении газообразных, жидких и твердых деформируемых тел. Основой МСС являются подходы и методы, развитые теоретической механикой, которая рассматривает движения материальной точки, дискретных систем материальных точек и абсолютно твердого тела с изменяющимися расстояниями между ними во время движения. Как и теоретическая механика, МСС инструментом исследования физических тел использует модели процессов или явлений. В ряде случает, например, при движении газов, процессы, проистекающие в деформируемых средах, тесно связаны с термодинамическими явлениями в этих средах. Поэтому в основе МСС лежат как законы теоретической механики, так и законы термодинамики. МСС является теоретической базой для таких дисциплин как гидромеханика ньютоновских и неньютоновских жидкостей, газовая динамика, подземная гидромеханика, теория упругости, теория пластичности. Основные положения Гипотеза сплошности Явления, рассматриваемые в МСС, носят макроскопический характер. Это позволяет не рассматривать молекулярное строение вещества, а рассматривать физические тела как сплошные среды. Газ, жидкость, твердое деформированное тело рассматривают как среду непрерывным образом заполняющая часть пространства, т.е. представляющая собой непрерывный континуум, состоящий из множества дискретных материальных точек. С физической точки зрения принятие модели сплошности означает, что при макроскопическом описании всякий «бесконечно малый объем» содержит достаточно большое число молекул. Например, кубик воздуха с ребром 10-3 мм содержит 2*106 молекул. Отсюда видено, что предлагаемая идеализация не будет применимой лишь при очень больших разряжения. Газ и жидкость называют жидкостью, только газ – сжимаемая, а капельная жидкость –несжимаемая жидкость. Области и разделы МСС МСС возникла в связи с решением таких задач, как установление закономерностей при истечении жидкостей из сосудов, просачивание жидкости через грунт, прогиба балок, находящихся под нагрузкой и т.д. С помощью и на основе методов и данных, развитых в теоретической механике, в МСС рассматриваются движение тел с изменяющимися расстояниями между точками этих тел во время движения. В настоящее время МСС (механику сплошной среды) разделяют на две крупные области МЖГ (механику жидкости и газа), которая именуется гидромеханикой, и МДТ механику твердо деформированного тела. Гидромеханика включает в себя следующие разделы: 1) механика идеальной жидкости; 2) механика вязкой жидкости (или ньютоновской жидкости); 3) механика невязкой жидкости (или неньютоновской жидкости); 4) механика турбулентных течений. К гидромеханике примыкают механика фильтрационных течений и ряд других разделов механики. Механика деформированных тел состоит из: 1) теория упругости; 2) теория пластичности; 3) теория ползучести;4) механика сыпучих тел. К МДТ примыкают теория прочности и механика разрушения. Такое разделение МСС связано с тем, что различные тела даже при одних и тех же условиях ведут себя по-разному. Поэтому определяющие параметры и функции, граничные условия и дифференциальные уравнения так же не одинаковы.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1547; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.161.115 (0.014 с.) |

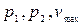 - начальное и конечное давление, максимальная скорость.
- начальное и конечное давление, максимальная скорость.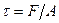 (2.1)
(2.1)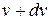 и внизу
и внизу 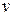 деформированного кубика к его высоте.
деформированного кубика к его высоте.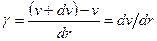 (2.2)
(2.2)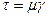 (2.3)
(2.3)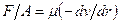 (2.4)
(2.4)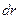 . На стенке находится (пристеночный) неподвижный слой.
. На стенке находится (пристеночный) неподвижный слой.
 (3.1)
(3.1) ,
,  (3.2)
(3.2)
 (3.3)
(3.3) (3.4)
(3.4) - субстанционная ли полная производная;
- субстанционная ли полная производная;  - локальная (местная) производная, характеризует изменение функции в данной точке пространства в единицу времени;
- локальная (местная) производная, характеризует изменение функции в данной точке пространства в единицу времени;  - конвективная производная, характеризующая изменение функции по координатам.
- конвективная производная, характеризующая изменение функции по координатам.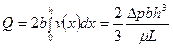 (4.1)
(4.1)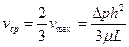 (4.2)
(4.2)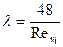 . (4.3)
. (4.3)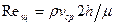 - параметр Рейнольдса для плоской щели;
- параметр Рейнольдса для плоской щели; 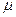 - динамическая вязкость [ Па•с ];
- динамическая вязкость [ Па•с ];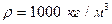 ,
, 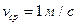 ,
, 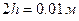 ,
, 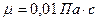 имеем:
имеем: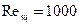 ;
; 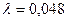 ;
; 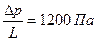 т.е. на каждые 1000 м гидравлические потери составят 1,2 МПа.
т.е. на каждые 1000 м гидравлические потери составят 1,2 МПа.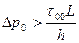 (4.4)
(4.4)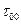 - статическое касательное напряжения сдвига у поверхности канала.
- статическое касательное напряжения сдвига у поверхности канала.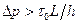 (4.5)
(4.5)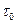 - динамическое касательное напряжения сдвига;
- динамическое касательное напряжения сдвига; 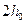 - жесткое ядро потока.
- жесткое ядро потока.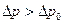 т.е. расчет параметров движущейся жидкости. Поэтому для неньютоновских жидкостей основные характеристики потока имеют вид:
т.е. расчет параметров движущейся жидкости. Поэтому для неньютоновских жидкостей основные характеристики потока имеют вид: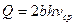 (4.6)
(4.6)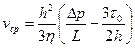 (4.7)
(4.7)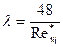 (4.8)
(4.8)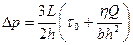 (4.9)
(4.9)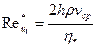 - обобщенный параметр Рейнольдса;
- обобщенный параметр Рейнольдса;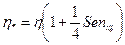 - приведенная вязкость жидкости Шведова-Бингама;
- приведенная вязкость жидкости Шведова-Бингама;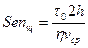 - параметр Сен-Венанна для плоской щели.
- параметр Сен-Венанна для плоской щели.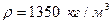 ,
, 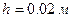 ,
, 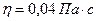
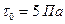 имеем:
имеем: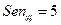 ;
; 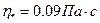 ;
; 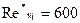 ;
; 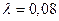 ;
; 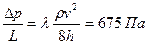 т.е. на каждые 1000 м гидравлические потери составят 0,675 МПа.
т.е. на каждые 1000 м гидравлические потери составят 0,675 МПа. , которые называются компонентами симметричного тензора деформаций.
, которые называются компонентами симметричного тензора деформаций. , с компонентами перемещениями
, с компонентами перемещениями  осуществляется через соотношение Коши:
осуществляется через соотношение Коши: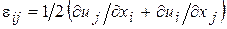 ,
, 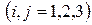 (5.1)
(5.1) , то для определения 3-х компонентов вектора перемещения
, то для определения 3-х компонентов вектора перемещения 
 (5.2)
(5.2)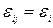 вдоль этих направлений без изменения прямых углов
вдоль этих направлений без изменения прямых углов  . Такие направления называются главными осями деформации, а величины
. Такие направления называются главными осями деформации, а величины  - главными удлинениями, которые могут быть найдены из следующего кубического уравнения:
- главными удлинениями, которые могут быть найдены из следующего кубического уравнения: (5.3)
(5.3) - компоненты девиатора деформаций;
- компоненты девиатора деформаций;  - текущая координата;
- текущая координата;  - символ Кронекера
- символ Кронекера 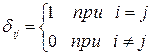 ;
;  - объемная деформация;
- объемная деформация;  - коэффициенты деформации.
- коэффициенты деформации.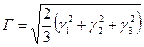 (5.4)
(5.4) ;
;  ;
;  - главные сдвиги.
- главные сдвиги.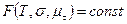 (5.19)
(5.19)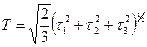 – интенсивность касательный напряжений;
– интенсивность касательный напряжений; 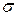 - среднее нормальное напряжение;
- среднее нормальное напряжение; 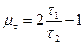 - параметр Лоде-Надаи, изменяется в пределах от (-1 до+1) и указывает на взаимоотношения главных нормальных напряжений.
- параметр Лоде-Надаи, изменяется в пределах от (-1 до+1) и указывает на взаимоотношения главных нормальных напряжений.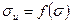 (5.20)
(5.20)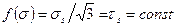 следует критерий Губера- Мизеса, основанный на гипотезе, что процесс разрушения зависит главным образом от изменения формы элемента тела:
следует критерий Губера- Мизеса, основанный на гипотезе, что процесс разрушения зависит главным образом от изменения формы элемента тела: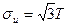 (5.21)
(5.21)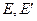 - модули Юнга по направлениям, параллельным и перпендикулярным напластованию;
- модули Юнга по направлениям, параллельным и перпендикулярным напластованию; 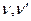 - коэффициенты Пуассона, характеризующие поперечное сжатие в плоскости напластования при сжатии в той же плоскости и в направлении перпендикулярном к ней.
- коэффициенты Пуассона, характеризующие поперечное сжатие в плоскости напластования при сжатии в той же плоскости и в направлении перпендикулярном к ней.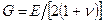 ,
, 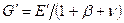 , (5.22)
, (5.22)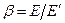 - основной параметр анизотропии.
- основной параметр анизотропии. . (5.23)
. (5.23)


