
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отчистка ствола скважины от шламаСодержание книги
Поиск на нашем сайте
Одна из основных функций борового раствора при бурении скважин – обеспечение выноса на дневную поверхность разрушенной на забое и осыпающейся со стенок породы (шлама). При этом качество очистки ствола скважины достигается надлежащим выбором режима промывки и свойств бурового раствора. В настоящее время теоретическое решение этой задачи состоит в определении средней скорости
где Условие (4.52) не гарантирует качество очистки, так как не является достаточным критерием. Это объясняется сложным характером движения частиц твердого тела в потоке жидкости и зависимостью этого движения от многих факторов. Гарантировать полный вынос шлама, поступающего в затрубное пространство, можно, если выполняется неравенство:
где Однако опыты свидетельствуют о том, что 100 % выноса шлама на поверхность не бывает. Соответственно частицы шлама могут занимать положения вне ядра выноса. Для течения жидкости Шведова-Бингама вероятность
Здесь
Определение скорости осаждения частиц Сила сопротивления, возникающая при движении частицы относительно жидкости, в общем случае определяется по зависимости:
где При установившемся движении частицы сила сопротивления должна быть уравновешена собственным весом частицы и выталкивающей силой
где Из равенства
где
Приведенные зависимости используются для вычисления относительной скорости движения частицы по известному коэффициенту сопротивления или для определения Сложность вычисления скорости осаждения частиц состоит в том, что при ее определении необходимо знать параметр В связи с этим, возможно получить приближенную, но достаточно обоснованную зависимость для определения
где Если в (4.60) подставить (4.58) то получим полезное соотношение вида:
где При медленном осаждении частицы, когда силы вязкости превосходят силы инерции (
Уравнения механики деформированного тела (МДТ) Элементы теории деформаций Характерной чертой движения сплошной среды является ее деформация т.е. изменение расстояния между отдельными точками среды. Как известно из теоретической механики деформация элементарного объема среды в окрестности рассматриваемой точки полностью определяется шестью величинами Связь компонентов тензоров деформации
Если известны компоненты деформации
Остальные уравнения получаются круговой заменой индексов (1-2-3-1). Таким образом, условие совместимости (5.2) является уравнениями, которые связывают компоненты тензора деформации В любой точке тела всегда существует, по крайней мере, одна тройная взаимно перпендикулярных направлений, таких, что деформация элемента в окрестности точки определяется только удлинением (укорочением)
где Характеристикой искажения формы элемента сплошной среды служит инвариантная величина, называемая интенсивностью деформации сдвига:
Здесь
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 659; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.166.151 (0.008 с.) |

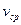 потока в затрубном пространстве из условия гидротранспорта шлама:
потока в затрубном пространстве из условия гидротранспорта шлама: (4.52)
(4.52) - скорость осаждения частицы шлама характерного размера
- скорость осаждения частицы шлама характерного размера  , относительно несущей ее жидкости.
, относительно несущей ее жидкости. (4.53)
(4.53) - скорость жидкости в точке расположения центра частицы, определяемого координатой
- скорость жидкости в точке расположения центра частицы, определяемого координатой  . Это возможно лишь при одном условии, когда каждая из частиц шлама расположена внутри яра выноса.
. Это возможно лишь при одном условии, когда каждая из частиц шлама расположена внутри яра выноса. выноса любой частицы шлама размером
выноса любой частицы шлама размером  . (4.54)
. (4.54) - параметр Сен-Венана для кольцевого сечения. Следовательно, ненулевая вероятность выноса возможна при средней скорости:
- параметр Сен-Венана для кольцевого сечения. Следовательно, ненулевая вероятность выноса возможна при средней скорости: (4.55)
(4.55) (4.56)
(4.56) - коэффициент сопротивления, который введен по аналогии с коэффициентом гидравлического сопротивления;
- коэффициент сопротивления, который введен по аналогии с коэффициентом гидравлического сопротивления;  - площадь сечения частицы, перпендикулярного в направлении ее движения (миделево сечение).
- площадь сечения частицы, перпендикулярного в направлении ее движения (миделево сечение). :
: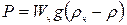 (4.57)
(4.57) - ускорение силы тяжести;
- ускорение силы тяжести;  - соответственно плотность частицы и жидкости;
- соответственно плотность частицы и жидкости;  - объем частицы.
- объем частицы. следует:
следует: ; (4.58)
; (4.58) , (4.59)
, (4.59) - параметр формы частицы.
- параметр формы частицы. .
. :
: (4.60)
(4.60) - динамический коэффициент вязкости жидкости.
- динамический коэффициент вязкости жидкости. (4.61)
(4.61) - параметр Архимеда.
- параметр Архимеда. ) удалось получить простое аналитическое решение:
) удалось получить простое аналитическое решение: ; (4.62)
; (4.62) . (4.63)
. (4.63) , которые называются компонентами симметричного тензора деформаций.
, которые называются компонентами симметричного тензора деформаций. , с компонентами перемещениями
, с компонентами перемещениями  осуществляется через соотношение Коши:
осуществляется через соотношение Коши: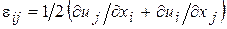 ,
, 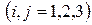 (5.1)
(5.1) , то для определения 3-х компонентов вектора перемещения
, то для определения 3-х компонентов вектора перемещения 
 (5.2)
(5.2)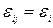 вдоль этих направлений без изменения прямых углов
вдоль этих направлений без изменения прямых углов  . Такие направления называются главными осями деформации, а величины
. Такие направления называются главными осями деформации, а величины  - главными удлинениями, которые могут быть найдены из следующего кубического уравнения:
- главными удлинениями, которые могут быть найдены из следующего кубического уравнения: (5.3)
(5.3) - компоненты девиатора деформаций;
- компоненты девиатора деформаций;  - текущая координата;
- текущая координата;  - символ Кронекера
- символ Кронекера 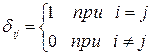 ;
;  - объемная деформация;
- объемная деформация;  - коэффициенты деформации.
- коэффициенты деформации.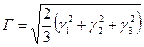 (5.4)
(5.4) ;
;  ;
;  - главные сдвиги.
- главные сдвиги.


