
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения трубопроводного участкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнение сохранения количества движения теплоносителя на участке трубы можно записать через массовый расход на выходе, а уравнение неразрывности - через давление на выходе:
где
где Элемент гидравлического сопротивления При наличии на выделенном участке нескольких местных сопротивлений, наряду с путевыми потерями, активное сопротивление можно определить так:
здесь: Коэффициент гидравлического сопротивления участка трубы определяется в общем случае как
Выражение для активного сопротивления при ламинарном режиме течения при
В гидравлических расчетах теплообменных аппаратов для турбулентного течения однофазной жидкости гидравлический коэффициент трения определяют по формуле Никурадзе:
Удовлетворительные результаты можно получить как при ламинарном, так и при турбулентном режиме течения, используя формулу Филоненко - Альтшуля:
Для гладких прямых участков при ламинарном неизотермическом течении, для круглого поперечного сечения канала,
при турбулентном неизотермическом потоке:
Коэффициент гидравлической массы
Для изогнутого участка индуктивное сопротивление L можно представить как сумму коэффициентов индуктивности, первый из которых связан с длиной участка вдоль оси
E.G. Jackson приводит значения зависимости для
а) б) Рис. 3.6. Зависимость инерции трубы от кривизны: ○ – скругленный поворот (а); ▲ – угловой поворот (б).
Коэффициент гидравлической емкости
Податливость трубопровода учитывается подстановкой в выражение (3.50) эффективного значения скорости звука
Аналогичное выражение для определения емкостного сопротивления можно записать как
Здесь значение эффективного модуля упругости
Коэффициент акустической формы
Уравнение энергии запишем по аналогии с уравнениями движения и неразрывности:
где Количество теплоты, переданное от внутренней поверхности стенки к жидкости и от жидкости к стенке, определяется через известную зависимость
где при нагреве В качестве уравнения состояния для капельной жидкости можно записать выражение, характеризующее изменение плотности под влиянием температуры:
Здесь 4. Задачи Гидромеханики в бурении Базовые задачи гидродинамики при промывке и цементировании скважин При промывке и цементировании скважин базовыми задачами гидромеханики, являются - задачи о течении жидкости в плоской щели (между двумя бесконечными параллельными пластинами); - задачи о течении жидкости в круглой трубе и кольцевом пространстве между двумя соосными цилиндрами. Решение этих задач производятся при следующих условиях: - жидкость несжимаема Ниже рассмотрим задачу о течении жидкости в плоской щели (между двумя бесконечными параллельными пластинами). Течение в щелевом канале Ламинарное течение ньютоновской жидкости основными характеристиками потока в щели являются: - объемный расход - средняя скорость - коэффициент сопротивления Здесь 2h – ширина щели; b – глубина щели; L – высота щели; Например, при
Ламинарное течение неньютоновской жидкости (Бингама) Схема профиля скорости в щелевом канале неньютоновской жидкости (Бингама) приведена на Рис. 8. Для неньютоновской жидкости Шведова-Бингама условие страгивания покоящейся жидкости является соотношение:
здесь Условием существования движения является соотношение:
здесь Для практических инженерных расчетов представляет интерес случаи, когда - объемный расход - средняя скорость - коэффициент сопротивления из уравнений (4.6, 4.7) можно выразить перепад давлений:
Здесь
Например, при
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 667; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.007 с.) |

 , (3.39)
, (3.39) ;
; 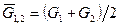 ;
;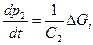 , (3.40)
, (3.40) .
.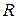 (активное сопротивление) характеризует диссипативные потери энергии при движении жидкости по участку трубы.
(активное сопротивление) характеризует диссипативные потери энергии при движении жидкости по участку трубы. , (3.41)
, (3.41) ,
,  - соответственно количества местных сопротивлений и гидравлических участков.
- соответственно количества местных сопротивлений и гидравлических участков. . (3.42)
. (3.42)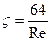 примет вид:
примет вид: . (3.43)
. (3.43)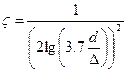 . (3.44)
. (3.44) . (3.45)
. (3.45) можно определить по формуле:
можно определить по формуле: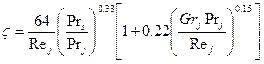 ; (3.46)
; (3.46)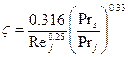 . (3.47)
. (3.47) (индуктивное сопротивление) характеризует инерционные свойства жидкости. Для цилиндрических элементов (труб) индуктивное сопротивление определится как
(индуктивное сопротивление) характеризует инерционные свойства жидкости. Для цилиндрических элементов (труб) индуктивное сопротивление определится как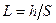 . (3.48)
. (3.48)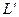 , а второй - с кривизной течения
, а второй - с кривизной течения  , т. е:
, т. е: . (3.49)
. (3.49)
 (емкостное сопротивление) характеризует свойство сжимаемости жидкости. В общем случае он определится как
(емкостное сопротивление) характеризует свойство сжимаемости жидкости. В общем случае он определится как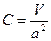 . (3.50)
. (3.50) в рабочей среде, вычисленной с учетом модулей упругости жидкости
в рабочей среде, вычисленной с учетом модулей упругости жидкости  и стенок
и стенок  трубы. Выражение для определения эффективной скорости звука имеет вид:
трубы. Выражение для определения эффективной скорости звука имеет вид: . (3.51)
. (3.51) . (3.52)
. (3.52) находится по формуле Н.Е. Жуковского:
находится по формуле Н.Е. Жуковского: . (3.53)
. (3.53) для тонкостенной цилиндрической трубы определиться как:
для тонкостенной цилиндрической трубы определиться как: . (3.54)
. (3.54) , (3.55)
, (3.55) - тепловой поток;
- тепловой поток;  - энтальпия теплоносителя;
- энтальпия теплоносителя;  - тепловая емкость жидкости;
- тепловая емкость жидкости;  - тепловой поток, подводимый
- тепловой поток, подводимый  к жидкости, и отводимый
к жидкости, и отводимый  от нее.
от нее.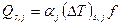 , (3.56)
, (3.56) ; при охлаждении
; при охлаждении  ,
,  .
. . (3.57)
. (3.57) - изменение температуры жидкости на выделенном участке трубы в единицу времени.
- изменение температуры жидкости на выделенном участке трубы в единицу времени. ; течение установившееся
; течение установившееся  ; все частицы жидкости движутся параллельно твердым стенкам канала (скважины, трубы), т.е. одномерное течение вдоль оси канала; концевые эффекты пренебрежимо малы т.е. поток в любом сечении идентичен; вдоль потока действует постоянный градиент давлений, равный
; все частицы жидкости движутся параллельно твердым стенкам канала (скважины, трубы), т.е. одномерное течение вдоль оси канала; концевые эффекты пренебрежимо малы т.е. поток в любом сечении идентичен; вдоль потока действует постоянный градиент давлений, равный  , где
, где 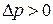 - полный перепад давлений между двумя сечениями, находящимися на расстоянии L.; на жидкость действует объемная сила, обусловленная только силой тяжести:
- полный перепад давлений между двумя сечениями, находящимися на расстоянии L.; на жидкость действует объемная сила, обусловленная только силой тяжести: 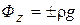 , при чем знак (+) – если жидкость движется вниз, (-) в верх, когда направление оси OZ совпадает с направлением движения.
, при чем знак (+) – если жидкость движется вниз, (-) в верх, когда направление оси OZ совпадает с направлением движения.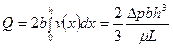 (4.1)
(4.1)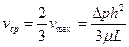 (4.2)
(4.2)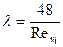 . (4.3)
. (4.3)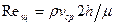 - параметр Рейнольдса для плоской щели;
- параметр Рейнольдса для плоской щели; 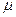 - динамическая вязкость [ Па•с ];
- динамическая вязкость [ Па•с ]; ,
, 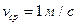 ,
, 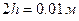 ,
, 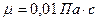 имеем:
имеем: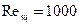 ;
; 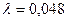 ;
; 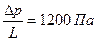 т.е. на каждые 1000 м гидравлические потери составят 1,2 МПа.
т.е. на каждые 1000 м гидравлические потери составят 1,2 МПа.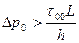 (4.4)
(4.4)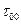 - статическое касательное напряжения сдвига у поверхности канала.
- статическое касательное напряжения сдвига у поверхности канала.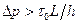 (4.5)
(4.5)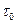 - динамическое касательное напряжения сдвига;
- динамическое касательное напряжения сдвига; 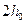 - жесткое ядро потока.
- жесткое ядро потока.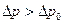 т.е. расчет параметров движущейся жидкости. Поэтому для неньютоновских жидкостей основные характеристики потока имеют вид:
т.е. расчет параметров движущейся жидкости. Поэтому для неньютоновских жидкостей основные характеристики потока имеют вид: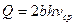 (4.6)
(4.6)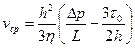 (4.7)
(4.7)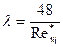 (4.8)
(4.8)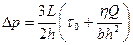 (4.9)
(4.9)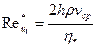 - обобщенный параметр Рейнольдса;
- обобщенный параметр Рейнольдса;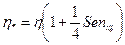 - приведенная вязкость жидкости Шведова-Бингама;
- приведенная вязкость жидкости Шведова-Бингама;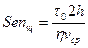 - параметр Сен-Венанна для плоской щели.
- параметр Сен-Венанна для плоской щели.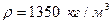 ,
, 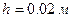 ,
, 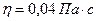
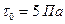 имеем:
имеем: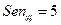 ;
; 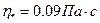 ;
; 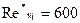 ;
; 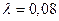 ;
; 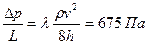 т.е. на каждые 1000 м гидравлические потери составят 0,675 МПа.
т.е. на каждые 1000 м гидравлические потери составят 0,675 МПа.


