
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матричные уравнения контурных токовСодержание книги
Поиск на нашем сайте
Уравнения контурных токов можно записать в матричной форме:
где
Матрица контурных сопротивлений
где
Рассмотрим схему, приведенную на рисунке 2.24. Направление обхода каждого контура совпадает с положительным направлением соответствующего контурного тока, а направление ветвей – с положительными направлениями токов в ветвях.
Рисунок 2.24 – Электрическая цепь постоянного тока
Граф электрической цепи, с выбранным деревом из четвертой, пятой и шестой ветви, приведен на рисунке 2.25.
Рисунок 2.25 – Граф цепи постоянного тока В данной схеме, независимые контуры содержат контурные токи Матрица контуров
Диагональная матрица сопротивлений Произведение матриц
Квадратная матрица контурных сопротивлений
Матрица-столбец контурных токов Матрица-столбец контурных ЭДС
Пользуясь матрицами Матрица токов ветвей Например, для электрической цепи (рис. 2.24):
Из этого матричного уравнения получаем равенства, определяющие токи ветвей через контурные токи:
Пример 2.9. Решить задачу, приведенную в примере 2.5 с помощью матричных уравнений контурных токов. Матрица контуров В состоит из пяти строк и десяти столбцов:
Диагональная матрица сопротивлений
Произведение матриц
Квадратная матрица контурных сопротивлений
Матрица-столбец контурных токов
Матрица-столбец контурных ЭДС
Определяем матрицу контурных токов
Контурные токи соответственно равны
Матрица токов ветвей
Токи в ветвях соответственно равны
Токи, рассчитанные в примерах 2.5 и 2.9, совпадают.
Метод узловых потенциалов
Метод узловых потенциалов для электрических Схем общего вида
Идея метода узловых потенциалов (МУП). Один из узлов схемы заземляется и его потенциал принимается равным нулю. Далее определяются потенциалы остальных узлов, что дает возможность определить напряжения на зажимах каждой ветви. Затем, используя закон Ома (рис. 2.26), определяем токи в ветвях. Запишем выражения закона Ома для различных участков цепи, приведенных на рисунке 2.26.
Рисунок 2.26. – Закон Ома: а) с источником напряжения; б) без источника напряжения
Для участка цепи, содержащего источник напряжения:
Для участка цепи, не содержащего источник напряжения:
Таким образом, для определения тока к ветвях, необходимо определить потенциалы узлов (напряжения на зажимах ветвей). Выведем систему уравнений для определения потенциалов узлов произвольной схемы. Для этого используем закон Ома и первый закон Кирхгофа. Допустим, имеется схема, приведенная на рисунке 2.27. Заземлим 3 узел, тогда потенциал φ3 = 0. Потенциалы остальных узлов будут соответственно φ1 и φ2.
Рисунок 2.27 – Электрическая цепь Используя закон Ома, запишем уравнения для токов в каждой ветви.
Уравнения по первому закону Кирхгофа для первого и второго узлов имеют вид:
В полученную систему уравнений подставим уравнения для токов, составленных по закону Ома. В результате получим:
Имеем два уравнения с двумя неизвестными потенциалами φ 1 и φ 2. Рассмотрим свойства полученных уравнений. При составлении первого уравнения потенциал φ1 умножается на сумму проводимостей ветвей, подсоединённых к этому узлу. Влияние потенциала второго узла осуществляется путем введения элемента В правой части уравнения записывается алгебраическая сумма токов источников питания ветвей, подсоединенных к данному узлу. Если ЭДС источника направлена к узлу, то произведение Используя вышеуказанные свойства запишем систему уравнений для определения потенциалов произвольной схемы. Допустим, имеется электрическая схема, содержащая n + 1 узлов. Заземляем один узел и имеем n неизвестных потенциалов (соответственно n уравнений).
где где
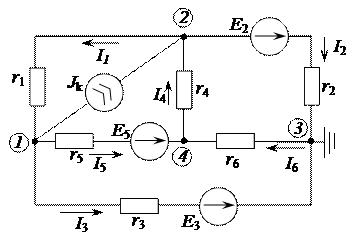
Пример 2.10. Рассмотрим рекомендованный порядок решения МУП на конкретном примере электрической цепи, приведенной на рисунке 2.28, с параметрами E3 = 30 (B), Е2 = 20 В, Е5 = 50 В, r1 = 20 Ом, r2 = 10 Ом, r3 = 8 Ом, r4 = 10 Ом, r5 = 10 Ом, r6 = 5 Ом, Jk = 3 А.
1. Осуществляем предварительный анализ схемы. Количество ветвей – Потенциал третьего узла принимаем равным нулю:
Рисунок 2.28 – Электрическая цепь постоянного тока
2. Составляем уравнения для определения потенциалов
3. Подставляем числовые значения и решаем систему уравнений. 3.1. Проводимости ветвей
3.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
Сумма проводимостей, соединяющих различные узлы
Узловые токи
3.2. После подстановки цифровых данных система имеет вид
3.3. Решая данную систему уравнений произвольным методом, определяем потенциалы:
3.4. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.28.
4. Определяем напряжение на зажимах источника тока. Из контура 121:
5. Проверяем решение системы уравнений, составив баланс мощностей. 5.1. Мощность источников:
Знак ”-” указывает на то, что третий источник работает в режиме потребителя электроэнергии (например, зарядка аккумулятора). Суммарная мощность источников:
4.2. Мощность приемников:
Суммарная мощность приемников:
4.3. Из сравнения генерируемой мощности источниками и потребляемой мощности приемниками, следует, что погрешность вычислении
Пример 2.11. Рассмотрим решение задачи, приведенной в примере 2.2, методом узловых потенциалов. Электрическая цепь для рассматриваемого метода, приведена на рисунке 2.29.
Рисунок 2.29 – Электрическая цепь постоянного тока
1. Осуществляем предварительный анализ схемы. Количество ветвей – Потенциал третьего узла принимаем равным нулю: 2. Составляем уравнения для определения потенциалов
3. Подставляем числовые значения и решаем систему уравнений. 3.1. Проводимости ветвей
3.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
Сумма проводимостей, соединяющих различные узлы
Узловые токи
3.2. После подстановки цифровых данных система имеет вид
3.3. Решая данную систему уравнений произвольным методом, определяем потенциалы:
3.4. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.29.
Токи в ветвях, рассчитанные в примерах 2.2 и 2.11, совпадают.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1811; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.73.117 (0.007 с.) |

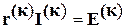 ,
, - квадратная матрица контурных сопротивлений;
- квадратная матрица контурных сопротивлений; - матрица-столбец контурных токов;
- матрица-столбец контурных токов; - матрица-столбец контурных ЭДС, учитывающая источники напряжений и эквивалентные ЭДС от источников тока.
- матрица-столбец контурных ЭДС, учитывающая источники напряжений и эквивалентные ЭДС от источников тока. :
: ,
, - диагональная матрица сопротивлений ветвей;
- диагональная матрица сопротивлений ветвей;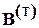 - транспортированная матрица контуров.
- транспортированная матрица контуров.

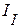 ,
, 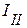 ,
, 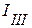 , что соответствует первой, второй и третьей ветвям связи.
, что соответствует первой, второй и третьей ветвям связи. .
.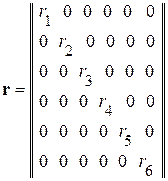 .
. .
.


 .
. .
. .
. определяется через матрицу контурных токов
определяется через матрицу контурных токов  .
.
 .
. ;
; 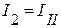 ;
;  ;
;  ;
;  ;
; 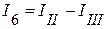 .
.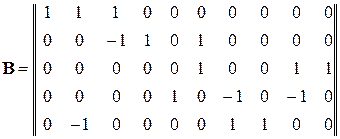 .
. .
.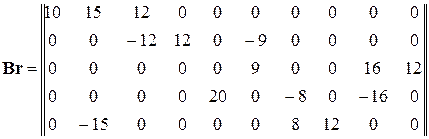 .
.

 .
. .
. .
. =
=
 .
. А,
А, 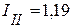 А,
А,  А,
А, А,
А,  А.
А.
 .
. А,
А,  А,
А,  А,
А,  А,
А,  А,
А, А,
А,  А,
А, 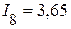 А,
А, 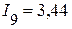 А,
А,  А.
А.
 .
.
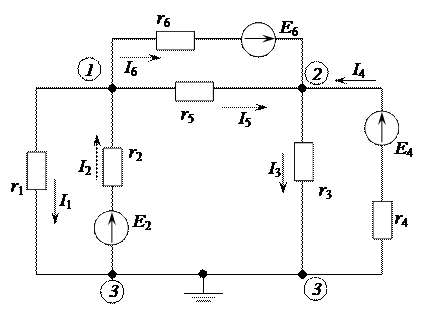
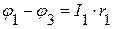 =>
=>  ,
, =>
=>  ,
, =>
=>  ,
, =>
=>  ,
, =>
=>  ,
, =>
=>  .
.

 . Этот элемент берется всегда со знаком ”-”. Слагаемое
. Этот элемент берется всегда со знаком ”-”. Слагаемое  является арифметической суммой проводимостей ветвей, соединяющих 1 и 2 узел.
является арифметической суммой проводимостей ветвей, соединяющих 1 и 2 узел. берется со знаком ”+”, если от узла – со знаком ”-“.
берется со знаком ”+”, если от узла – со знаком ”-“.
 ,
,  ,
,  , …,
, …, 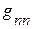 – соответственно сумма проводимостей ветвей, подсоединённых соответственно к 1, 2 … n – ному узлу (всегда со знаком +).
– соответственно сумма проводимостей ветвей, подсоединённых соответственно к 1, 2 … n – ному узлу (всегда со знаком +). и
и  – сумма проводимостей ветвей, соединяющих непосредственно 1 и 2 узел и т.д.
– сумма проводимостей ветвей, соединяющих непосредственно 1 и 2 узел и т.д. – сумма токов источников питания.
– сумма токов источников питания. , количество узлов –
, количество узлов –  .
. . Следовательно, необходимо определить потенциалы
. Следовательно, необходимо определить потенциалы  ,
,  ,
,  .
.

 См;
См; См;
См;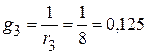 См;
См;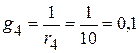 См;
См; См;
См;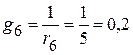 См.
См. См;
См; См;
См; См.
См. См;
См; См;
См;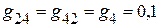 См.
См. А,
А, А,
А, А.
А.
 В,
В, В,
В, В.
В. А,
А, А,
А, А,
А, А,
А, А,
А,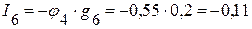 А.
А.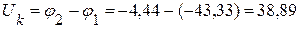 В.
В.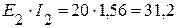 Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт.
Вт.
 Вт.
Вт. Вт,
Вт,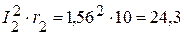 Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт.
Вт.
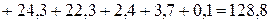 Вт.
Вт. и не превышает 0,5%.
и не превышает 0,5%.
 , количество узлов –
, количество узлов – 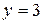 .
.
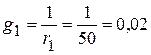 См;
См; См;
См; См;
См; См;
См; См.
См. См;
См; См.
См. См.
См. А,
А, А.
А.
 В,
В, В.
В. мА,
мА,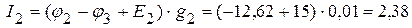 мА,
мА,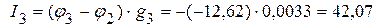 мА,
мА, мА,
мА, мА.
мА.


