
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения для описания процессов электрической цепи. Законы КирхгофаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Процессы, происходящие в электрических цепях, могут быть описаны системой уравнений состояния. Такими являются законы Кирхгофа. Первый закон Кирхгофа:алгебраическая сумма токов ветвей, подсоединённых к одному узлу, равняется нулю: Для каждого узла принимают положительное и отрицательное направление тока в подсоединенных ветвях (например, если ток направлен к узлу, то перед соответствующим током ставят знак «+», если ток направлен от узла то – знак «-»). Уравнения, составленные по первому закону Кирхгофа для электрической цепи, приведенной на рисунке 1.18, имеют вид:
Если просуммировать приведенные выше уравнения для первого, второго и третьего узлов, то полученная сумма будет равна выражению, составленному по первому закону Кирхгофа для четвертого узла – Следовательно, число независимых уравнений, составляемых по первому закону Кирхгофа равно ( Второй закон Кирхгофа: алгебраическая сумма напряжений ветвей произвольного контура равна нулю. Число независимых уравнений схемы равно числу главных контуров. Уравнения для остальных контуров могут быть получены из уравнений независимых контуров. При составлении уравнений, составленных по второму закону Кирхгофа пользуются следующим правилом:если положительное направление обхода контура и направление тока на элементе совпадают, то напряжение в соответственной ветви принимается со знаком «+», если не совпадает – то со знаком «–». Составим уравнения по второму закону Кирхгофа для электрической цепи, приведенной на рисунке 1.18:
Уравнения, составленные по второму закону Кирхгофа, могут быть описаны с использованием напряжений на элементах ветвей, входящих в контур. В этом случае второй закон Кирхгофа звучит так: алгебраическая сумма напряжений на элементах произвольного контура, равна алгебраической сумме ЭДС этого контура.
Уравнения, полученные по первому и второму законам Кирхгофа, позволяют описать процессы в электрической схеме в любой момент времени. Их число равно количеству ветвей. Для данной схемы - 6. Характер полученной системы уравнений – интегрально-дифференциальный. Если уравнение состоит только из резистивных элементов, то система уравнений имеет алгебраический характер.
Задачи расчета электрических цепей
В любой электрической цепи имеются исходные данные и данные, которые необходимо рассчитать. Задача считается решенной, если число уравнений равно числу неизвестных параметров цепи. Принято считать основной задачей расчета электрической цепи тот случай, при котором, при заданных значениям пассивных элементов (r, L, C) и заданных значениях активных элементов (i(t), e(t)), необходимо рассчитать токи в каждой ветви электрической схемы. Формы расчета задачи могут меняться, например, подобрать r таким образом, чтобы ток в цепи равнялся определенному значению i.
ЦЕПИ ПОСТОЯННОГО ТОКА
Особенностью цепей постоянного тока является тот факт, что пассивными элементами являются резистивные элементы, поэтому уравнение состояния электрических цепей (первый и второй законы Кирхгофа), представляет собой систему алгебраических уравнений. В данном разделе рассмотрим различные методы расчета и анализа электрических цепей с линейными резистивными элементами.
Применение законов Кирхгофа для расчета и анализа электрических цепей
Использования законов Кирхгофа для схем с Источниками напряжений
Допустим, имеем электрическую цепь постоянного тока, представленную на рисунке. 2.1.
Рисунок 2.1 – Электрическая цепь постоянного тока
Рассмотрим возможности решения основной задачи расчета приведенной разветвленной цепи постоянного тока. Исходными данными для расчета являются параметры активных и пассивных элеметов цепи. Требуется рассчитать токи в ветвях Рассмотрим основные этапы расчета и анализа. 1. Осуществляем предварительный анализ схемы. 1.1. Определяем количество ветвей и узлов схемы, выбираем положительное направление токов в ветвях (рис. 2.1). Количество ветвей - 1.2. Вычерчиваем граф схемы, в котором выделяем ветви дерева и ветви связи. Для данной схемы граф имеет вид, представленный на рисунке 2.2. Ветвями дерева приняты ветви 4,5,6. Ветви связи (1,2,3) обозначены на схеме пунктирными линиями.
Рисунок 2.2 – Граф исходной электрической цепи
1.3. Используя граф схемы, формируем независимые (главные) контуры. В контур входит одна ветвь связи, добавленная ветвями дерева. При формировании первого независимого контура используем 1 -ю ветвь связи, дополненную 4 и 5 ветвями дерева. Соответственно, второй главный контур состоит из ветви связи 2, дополненной 4 и 6 ветвями дерева; третий главный контур состоит из ветви связи 3, дополненной 5 и 6 ветвями дерева. Положительное направление обхода контура рекомендуется принимать совпадающим с направлением тока в ветви связи (рис. 2.1 и рис. 2.2.). Число независимых контуров для данной схемы равно 2. Составляем уравнения по законам Кирхгофа. 2.1. По первому закону Кирхгофа. При составлении уравнений учитываем правило знаков. Если ток направлен к узлу, то берем знак ”+”, если от узла, то принимаем знак ”-”. Либо наоборот. По первому закону Кирхгофа:
Таким образом, по первому закону Кирхгофа составлено ( 2.2. По второму закону Кирхгофа. При составлении используют следующее правило знаков. Если направление обхода контура и направление токов в ветви совпадают, то падение напряжения на резистивных элементах ветви берется со знаком ”+”. При несовпадении – знак ”-”. Аналогично учитываются знаки ЭДС источников напряжения. По второму закону Кирхгофа:
Таким образом, по второму закону Кирхгофа составлено В результате имеем систему из 6 уравнений и 6 неизвестных токов, что позволяет осуществить расчет токов в ветвях исходной схемы. Пример 2.1. Рекомендованный порядок расчета рассмотрим на примере электрической схемы, приведенной на рисунке 2.3, параметры которой равны: E 1 = 30 B, Е 2 = 20 В, Е 3 = 20 В, r 1 = 5 Ом, r 2 = 10 Ом, r 3= 8 Ом, r 4 = 8 Ом, r5 = 10 Ом, r 6 = 5 Ом.
Рисунок 2.3 – Электрическая цепь
1. Осуществляем предварительный анализ схемы. 1.1. Количество ветвей – 1.2. Вычерчиваем граф схемы, в котором выделяем ветви дерева и ветви связи. Для данной схемы граф имеет вид, представленный на рисунке 2.4. Ветвями дерева приняты ветви 4,5,2. Ветви связи (1,3,6) обозначены на схеме пунктирными линиями.
Рисунок 2.4 – Граф исходной электрической цепи
1.3. Используя граф схемы, формируем независимые (главные) контуры. При формировании первого независимого контура используем 1 -ю ветвь связи, дополненную 4 и 2 ветвями дерева. Соответственно, второй главный контур состоит из ветви связи 3, дополненной 2 и 5 ветвями дерева; третий главный контур состоит из ветви связи 6, дополненной 5 и 4 ветвями дерева. Положительное направление обхода контура принимаем совпадающим с направлением тока в ветви связи (рис. 2.3 и рис. 2.4). 2. Составляем уравнения по законам Кирхгофа. 2.1. По первому закону Кирхгофа:
2.2. По второму закону Кирхгофа:
3. Подставляем числовые значения в полученную систему уравнений:
Решая данную систему уравнений, определяем токи в ветвях:
4. Проверку решения системы уравнения осуществляем с помощью баланса мощности. 4.1. Мощность, генерируемая источниками:
Суммарная мощность источников:
4.2. Мощность приемников:
Суммарная мощность приемников:
4.3. Из сравнения генерируемой мощности источниками и потребляемой мощности приемниками, следует, что погрешность вычислений Пример 2.2. Рассмотрим пример электрической цепи, с последующей экспериментальной проверкой на стенде УИЛС, приведенной на рисунке 2.5, параметры которой равны: E 1 = 20 B, Е 2 = 15 В, r 1 = 50 Ом, r 2 = 100 Ом, r 3= 300 Ом, r 4 = 200 Ом, r5 = 150 Ом.
Рисунок 2.5 – Электрическая цепь постоянного тока
1. Осуществляем предварительный анализ схемы. 1.1. Количество ветвей – 1.2. Вычерчиваем граф схемы, в котором выделяем ветви дерева и ветви связи. Для данной схемы граф имеет вид, представленный на рисунке 2.6. Ветвями дерева приняты ветви 2,4. Ветви связи (1,3,5) обозначены на схеме пунктирными линиями.
Рисунок 2.6 – Граф исходной электрической цепи
1.3. Используя граф схемы, формируем независимые (главные) контуры. При формировании первого независимого контура используем 1 -ю ветвь связи, дополненную 4 ветвью дерева. Соответственно, второй главный контур состоит из ветви связи 5, дополненной 2 и 4 ветвями дерева; третий главный контур состоит из ветви связи 3, дополненной 2 ветвью дерева. Положительное направление обхода контура принимаем совпадающим с направлением тока в ветви связи (рис. 2.5 и рис. 2.6). 2. Составляем уравнения по законам Кирхгофа. 2.1. По первому закону Кирхгофа:
2.2. По второму закону Кирхгофа:
3. Подставляем числовые значения в полученную систему уравнений:
Решая данную систему уравнений, определяем токи в ветвях:
4. Проверку решения системы уравнения осуществляем с помощью баланса мощности. 4.1. Мощность, генерируемая источниками:
Суммарная мощность источников:
4.2. Мощность приемников:
Суммарная мощность приемников:
4.3. Из сравнения генерируемой мощности источниками и потребляемой мощности приемниками, следует, что погрешность вычислений
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 589; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

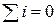 .
.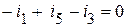 (1 узел);
(1 узел); (2 узел);
(2 узел); (3 узел);
(3 узел); (4 узел).
(4 узел).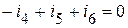 .
. ).
). (I контур);
(I контур); (II контур);
(II контур);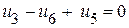 (III контур).
(III контур). (I контур);
(I контур); (II контур);
(II контур);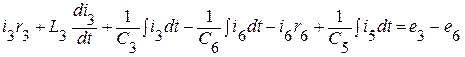 (III контур).
(III контур).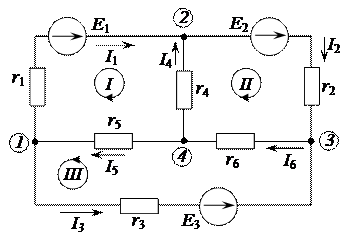
 ,
, 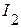 ,
,  ,
,  ,
, 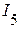 ,
,  . Используя первый и второй законы Кирхгофа можно составить систему из шести уравнений с шестью неизвестными токами, что позволяет решить поставленную задачу.
. Используя первый и второй законы Кирхгофа можно составить систему из шести уравнений с шестью неизвестными токами, что позволяет решить поставленную задачу. , количество узлов -
, количество узлов -  .
.
 .
. (1 узел);
(1 узел); (2 узел);
(2 узел); (3 узел).
(3 узел).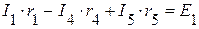 (I контур);
(I контур); (II контур);
(II контур); (III контур).
(III контур). независимых уравнений.
независимых уравнений.
 , количество узлов –
, количество узлов –  . Выбираем положительное направление токов в ветвях (рис. 2.3).
. Выбираем положительное направление токов в ветвях (рис. 2.3).
 (1 узел);
(1 узел); (2 узел);
(2 узел); (3 узел).
(3 узел). (I контур);
(I контур); (II контур);
(II контур); (III контур).
(III контур).
 А,
А,  А,
А,  А,
А, А,
А,  А,
А,  А.
А.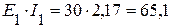 Вт,
Вт, Вт,
Вт, Вт.
Вт. Вт.
Вт. Вт,
Вт,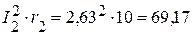 Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт,
Вт, Вт.
Вт.
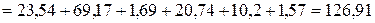 Вт.
Вт. и не превышает 0,5%.
и не превышает 0,5%.
 , количество узлов –
, количество узлов – 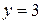 . Выбираем положительное направление токов в ветвях (рис. 2.5).
. Выбираем положительное направление токов в ветвях (рис. 2.5).
 (1 узел);
(1 узел); (2 узел).
(2 узел). (I контур);
(I контур); (II контур);
(II контур);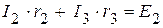 (III контур).
(III контур).
 мА,
мА, 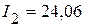 мА,
мА, 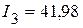 мА,
мА, мА,
мА,  мА.
мА.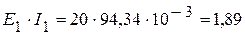 Вт,
Вт,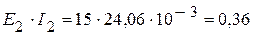 Вт.
Вт.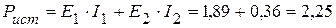 Вт.
Вт. Вт,
Вт,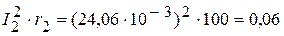 Вт,
Вт,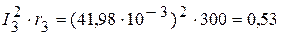 Вт,
Вт, Вт,
Вт,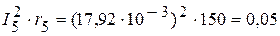 Вт.
Вт.
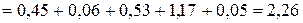 Вт.
Вт.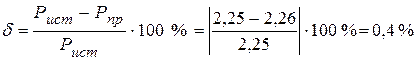 и не превышает 0,5%.
и не превышает 0,5%.


