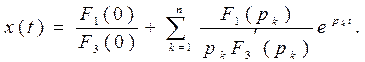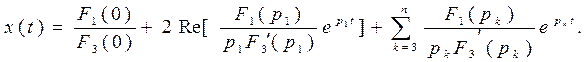Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Переходные процессы в линейных электрических цепях с сосредоточенными параметрамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы Исследовать переходные процессы в цепи с последовательным соединением R, L, C на физической модели и в среде EWB 5.12. Изучить методы расчета переходных процессов в электрических цепях с сосредоточенными параметрами и их применение для анализа процессов в линейных цепях.
Теоретическое введение Переходным называется процесс, возникающий в электрической цепи при переходе из одного установившегося состояния в другое. В установившихся режимах токи ветвей (iy) и напряжения (uy) на элементах схемы при заданной конфигурации линейной электрической цепи определяются только видом источников напряжения и тока. Эти величины рассчитываются методами анализа установившихся режимов и являются частным решением дифференциального уравнения цепи
(1)
где х – обычно ток индуктивности или напряжение на ёмкости; n – порядок дифференциального уравнения (определяется конфигурацией цепи и характером её элементов, равен или меньше количества индуктивных элементов и емкостей в схеме), f(t) – воздействие на схему (источник энергии). Для отыскания переходных токов i(t) и напряжений u(t) необходимо найти полное решение неоднородного дифференциального уравнения (1), которое рассматривается как сумма частного решения (принуждённая составляющая) и решения однородного дифференциального уравнения (свободная составляющая iсв), если принять заданные источники равными нулю i =iy + iсв. (2) Свободный ток возникает вследствие того, что при включении или отключении цепи или любом другом внезапном изменении в ней (коммутации) энергии в магнитных полях индуктивностей и электрических полях конденсаторов предыдущего установившегося режима не соответствуют аналогичным величинам нового установившегося состояния. Электрические цепи обладают активным сопротивлением, следовательно при t → ∞ iсв → 0 и i → iy. Решение однородного дифференциального уравнения
(3)
(4)
где pk – корни характеристического уравнения, Ak – постоянные интегрирования, значения которых определяются из физических начальных условий. Из уравнения (4) следует, что каждому корню в свободной составляющей соответствует собственная функция. Характеристическое уравнение
(5)
получают из однородного уравнения заменой символов дифференцирования сомножителем p, а символов интегрирования – сомножителем 1/p. Если имеется m кратных корней характеристического уравнения, т.е. p1 = p2 =...= pm, то соответствующие им собственные функции имеют вид
(6)
Если имеется пара комплексно сопряженных корней pk,k+1=-ak ± jwk (ak – собственное затухание, wk – собственная частота), то соответствующая ей собственная функция принимает вид
где yk, Ak – постоянные интегрирования.
. (8)
Основная трудность решения последнего уравнения – определение постоянных интегрирования. Их расчёт основан на знании начальных условий и законов коммутации. Под коммутацией понимают любое изменение в цепи, приводящее к возникновению переходного процесса или изменению режима её работы. Считается, что эти изменения (включение или отключение приёмника от источника; скачкообразное изменение параметров цепи; амплитуды, частоты или фазы приложенного напряжения; замыкания фаз или обрывы линейных проводов и т.д.) происходят мгновенно. В реальных условиях время коммутации всегда конечно и определяется быстродействием коммутационной аппаратуры (время срабатывания реле или выключателя и т.д.).
Начало отсчёта совмещают с моментом коммутации и обозначают через t = 0- - время до коммутации. Момент времени после коммутации обозначают t = 0+. Анализ электрических цепей для этих моментов времени проводят по до и после коммутационным схемам. Так как напряжения и токи в реальных электрических цепях всегда конечны, то и мгновенная мощность также конечна. Отсюда следует, что в таких цепях невозможно скачкообразное изменение энергий электрических и магнитных полей, т.е. ∆W = W(0+) - W(0-) = 0 и W(0+) = W(0-). (9) Энергия магнитного поля одиночной индуктивной катушки и энергия магнитного поля одиночного конденсатора равны, соответственно, WM = LiL2/2 и WЭ = Cu2C /2. (10) Это означает, что на интервале времени от t = 0- до t = 0+ должны выполняться равенства iL(0+) = iL(0-), uC(0+) = uC(0 -), (11) которые называются первый и второй закон коммутации: - ток индуктивности в первый момент после коммутации равен току индуктивности до коммутации и начинает плавно изменяться с этого значения; - напряжение на конденсаторе в первый момент после коммутации равно напряжению до коммутации и начинает плавно изменяться с этого значения. В такой формулировке эти законы не выполняются для случая мгновенного изменения индуктивности или ёмкости цепи. Если токи индуктивностей и напряжения на конденсаторах до коммутации были равны нулю, то имеют место нулевые начальные условия. Следовательно, в первый момент после коммутации индуктивность необходимо рассматривать как участок с бесконечно большим сопротивлением (обрыв), а конденсатор как участок с нулевым сопротивлением (коротко замкнутый участок). Если токи индуктивностей и напряжения на конденсаторах до коммутации не равны нулю, то имеют место ненулевые начальные условия. Следовательно, в первый момент после коммутации индуктивность необходимо рассматривать как идеальный источник тока (направление источника совпадает с направлением тока ветви), а конденсатор как идеальный источник ЭДС, направление которого противоположно направлению тока ветви. Рассмотренные начальные условия служат для определения произвольных постоянных интегрирования АК и ψК. Уравнение (8) справедливо на интервале времени от t= 0+ до t = ∞. Рассматривая это уравнение и его производные до n-1 включительно и подставляя в них начальные значения переходной величины и её производные, получим систему n линейных алгебраических уравнений с n неизвестными величинами АК и ψК. Изложенный метод анализа переходных процессов называется классическим. Для решения задач на переходные процессы при коммутации в разветвленных линейных цепях любым методом необходимо составить дифференциальное уравнение относительно искомой величины x. Для каждой из ветвей после коммутационной схемы составляется система уравнений по первому и второму законам Кирхгофа, которая исключением промежуточных переменных приводится к одному неоднородному дифференциальному уравнению n -го порядка относительно искомой величины. При этом несколько индуктивностей, включенных последовательно, и несколько конденсаторов, включенных параллельно, целесообразно заменить их эквивалентами. Можно составлять дифференциальные уравнения для контурных токов и узловых потенциалов, тогда число уравнений будет равно числу независимых контуров или числу узлов цепи без единицы. Это уменьшает порядок дифференциального уравнения. Порядок дифференциального уравнения уменьшается также на число узлов, к которым подходят только ветви с индуктивностями, и на число контуров, ветви которых содержат только конденсаторы (рис. 1).
L1 C1 C2
C3 C4 L2 L3
Рис. 1
(12)
которое ставит в соответствие оригиналу f(t) его изображение F(p); р = σ + jη – комплексное число, которое называют оператором. Условно преобразование Лапласа можно записывать в виде F(p) = L[f(t)]; F(p) Оригинал f(t) должен удовлетворять условиям Дирихле и при t > 0
Прямое преобразование Лапласа заменяет операции дифференцирования и интегрирования функции времени f(t) алгебраическими операциями умножения и деления на оператор р изображений этих функций:
Достоинство операторного метода расчёта переходных процессов, заключающегося в алгебраизации дифференциальных уравнений цепи, особенно проявляется при анализе сложных электрических цепей. Уравнения относительно изображений напряжения и тока произвольной цепи могут быть получены по законам Ома и Кирхгофа в операторной форме записи
составленных для операторных схем замещения. При составлении операторной схемы замещения произвольной цепи (рис. 2,а) индуктивности заменяются последовательно соединенными операторным сопротивлением pL и совпадающим по направлению с током источником ЭДС Li(0_), где i(0_) – начальное значение тока индуктивности; емкости заменяются последовательным соединением операторного сопротивления 1/pC и направленного встречно с напряжением на емкости источника ЭДС uC (0_)/p, где uC (0_) – начальное значение напряжения на емкости (рис. 1,б). При нулевых начальных условиях дополнительные источники ЭДС на операторной схеме отсутствуют.
Рис. 2
Система алгебраических операторных уравнений для разветвленных цепей путем исключения промежуточных переменных преобразуется к одному уравнению относительно искомой величины (напряжения или тока), из которого определяется изображение для искомой величины. Для всех технически реализуемых цепей изображение искомой величины имеет форму рациональной дроби
(15)
где p1, p2,..., pn – корни характеристического уравнения. Если корни характеристического уравнения различны, то оригинал определяется выражением
(16)
Если имеется один нулевой корень, т.е. F2(p)=pF3(p), то оригинал находится по формуле
(17)
Если имеются комплексные сопряжённые корни (p1,2 = -a1 ± jw1), то оригинал находится по формуле
(18)
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 634; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.219.213 (0.008 с.) |



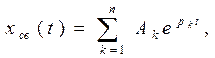 есть сумма экспонент
есть сумма экспонент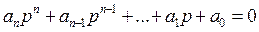
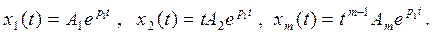
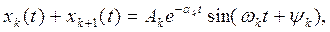 (7)
(7) Общее решение дифференциального уравнения представляется как сумма принужденной и свободной составляющих
Общее решение дифференциального уравнения представляется как сумма принужденной и свободной составляющих
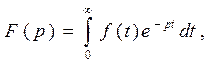 К дифференциальному уравнению (1) можно применить интегральное преобразование Лапласа (прямое преобразование Лапласа)
К дифференциальному уравнению (1) можно применить интегральное преобразование Лапласа (прямое преобразование Лапласа)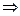 f(t).
f(t). , σ > α.
, σ > α. (13)
(13)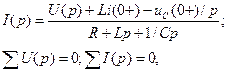 (14)
(14)