
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы теории электрических цепейСодержание книги
Поиск на нашем сайте
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ МОСКОВСКИЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ В.В. ФИЛИНОВ ОСНОВЫ ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ УЧЕБНОЕ ПОСОБИЕ по курсу "Электрические цепи и сигналы" для студентов, обучающихся: по специальности 10.05.02 «Информационная безопасность по специальности 10.05.03 «Информационная безопасность по направлению 10.03.01 «Информационная безопасность», МОСКВА МИРЭА‑МГУПИ 2016 УДК 621.38 ББК К95 Б19 Утверждено редакционно-издательским советом МГТУ МИРЭА Подготовлено на кафедре "Электротехника и электроника" (ОП–4) – МГУПИ Рецензент: д.т.н., профессор кафедры «Электротехника и интроскопия» МЭИ (Национальный исследовательский университет) Филинов В.В. Б19 Основы теории электрических цепей: учебное пособие / ISBN 978-5-7339- Учебное пособие предназначено для самостоятельного изучения основных разделов теории цепей. В данном учебном пособии рассматриваются вопросы анализа линейных, нелинейных и магнитных цепей, находящихся под воздействием гармонических, периодических негармонических, непериодических колебаний. Учебное пособие полезно для студентов (бакалавров и специалистов) специальностей и направлений информационной безопасности, слушающих курс лекций «Электротехника», «Теория электрических цепей». Может использоваться для изучения лекционных материалов по разделам «Радиотехнические цепи сигналы», «Цифровая обработка сигналов», выполнения практиеских,
Компьютерная верстка: Головченко Д.А., Карамышева Е.О., Третяк Е.В.
ISBN 978-5-7339-
© Филинов В.В, 2016 © МГТУ МИРЭА, 2016 ОГЛАВЛЕНИЕ Глава 1. Электрические цепи. 6 1.1. Ток, напряжение, мощность и энергия. 6 1.2. Элементы электрических цепей и их уравнения. 10 1.3. Классификация электрических цепей и режимов работы.. 18 1.4. Четырехполюсники. 26 1.5. Законы и методы анализа цепей. 31 1.5.1. Законы электротехники. 31 1.5.2. Методы анализа цепей. 35 1.6. Вопросы и задания для самопроверки. 39 Глава 2. Электрические цепи постоянного тока. 40 2.1. Электрическая цепь и элементы цепи. 40 2.2. Методы преобразования цепи. 42 2.2.1. Источник, нагруженный на резистор. 42 2.2.2. Закон Кирхгофа. 43 2.2.3. Последовательное соединение сопротивлений. 44 2.2.4. Параллельное соединение сопротивлений. 45 2.2.5. Преобразование схемы «звезда» в «треугольник» и обратно. 46 2.3. Методы расчета электрических цепей. 47 2.3.1. Метод непосредственного применения закона Ома. 47 2.3.2. Метод эквивалентных сопротивлений. 48 2.3.3. Метод суперпозиции (наложения) токов. 50 2.3.4. Метод непосредственного применения законов Кирхгофа. 51 2.3.5. Метод контурных токов. 54 2.3.6. Метод узловых напряжений. 56 2.3.7. Метод двух узлов (частный случай метода узловых напряжений)..60 2.3.8. Метод эквивалентного генератора (активного двухполюсника) 61 2.4. Коэффициент передачи резистивной цепи. 64 2.5. Методы анализа нелинейных электрических цепей. 68 2.5.1. Виды, характеристики и параметры нелинейных элементов. 68 2.5.2. Графические методы анализа нелинейных электрических цепей. 69 2.5.3. Аналитические методы анализа нелинейных электрических цепей.. 74 2.6. Вопросы и задания для самопроверки. 78 Глава 3. Электрические цепи при гармоническом токе. 81 3.1. Гармонические колебания. 81 3.1.1. Получение синусоидальной ЭДС.. 81 3.1.2. Основные величины, характеризующие синусоидальные функции времени………………………………………………………………………………….82 3.2. Формы представления гармонических колебаний. 87 3.3. Законы Ома и Кирхгофа в комплексной форме. 93 3.3.1. Цепь синусоидального тока с резистивным элементом. 94 3.3.2. Цепь синусоидального тока с индуктивным элементом. 96 3.3.3. Цепь синусоидального тока с емкостным элементом. 99 3.3.4. Цепь синусоидального тока с последовательно соединенными активным и реактивным сопротивлениями. 102 3.3.5. Цепь переменного синусоидального тока с последовательно соединенными элементами R, L, C.. 105 3.3.6. Электрическая цепь переменного синусоидального тока с параллельно соединёнными элементами R, L, C.. 110 3.4. Мощность в цепях гармонических колебаний. 115 3.5. Расчёт разветвленных цепей гармонического тока. 118 3.5.1. Расчёт цепей синусоидального тока. 118 3.5.2. Расчёт цепей с несколькими источниками. 120 3.6. Комплексные передаточные функции. 125 3.7. Вопросы и задания для самопроверки. 128 Глава 4. Электрические цепи несинусоидального тока. 129 4.1. Цепи с несинусоидальным током. 129 4.1.1. Расчет линейных цепей при несинусоидальных напряжениях 4.1.2. Электрические фильтры.. 136 4.2. Цепи с нелинейными элементами. 140 4.2.1. Резистивные нелинейные элементы.. 140 4.2.2. Расчет спектрального состава тока в резистивном нелинейном элементе при гармоническом воздействии. 144 4.3. Вопросы и задания для самопроверки. 154 Глава 5. Переходные процессы в линейных электрических цепях……………….156 5.1. Переходные процессы в цепи с последовательным соединением элементов R, L, C ………………………………………………………………….…. 158 5.2. Заряд конденсатора через резистор. 161 5.3. Разряд конденсатора через резистор. 163 5.4. Подключение индуктивности к источнику постоянной ЭДС через резистор........... 164 5.5. Вопросы и задания для самопроверки. 166 Глава 6. Электрические цепи с индуктивной связью.. 168 6.1. Параметры индуктивной связи. 168 6.2. Расчет цепей с индуктивной связью.. 172 6.3. Расчет цепей с электромагнитной связью.. 175 6.4. Вопросы и задания для самопроверки. 179 Глава 1. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ По количеству выводов ЭЦ. Двухполюсник — часть электрической цепи с двумя выделенными выводами Четырехполюсник (проходной) — часть электрической цепи с двумя парами выделенных выводов ( Рис. 1.18. а) двухполюсник, б) четырехполюсник Электрическая цепь (рис. 1.19, а) в зависимости от значения сопротивления нагрузки может работать в различных характерных режимах: номинальном, согласованном, холостого хода и короткого замыкания. Рис. 1.19. Режимы работы электрической цепи Эффективность работы ЭЦ в этих режимах оценивает коэффициент полезного действия (КПД) электрической цепи — это отношение мощности приемника (полезной)
Рассмотрим особенности этих режимов: 1. Номинальный режим электрической цепи (н). Это расчетный режим, Изоляция источника, линии передачи, приемников рассчитана на определенное напряжение, называемое номинальным. Параметры номинального режима указываются в паспорте устройства и обозначаются индексом «н», например, номинальное напряжение — 2. Согласованный режим работы простейшей цепи (с). Однако в согласованном режиме КПД низкий ( 3. Режим холостого хода и режим короткого замыкания. Эти режимы являются предельными режимами работы электрической цепи. В режиме холостого хода (х.х.) внешняяцепь разомкнута (рис. 1.19, б) и ток Так как Из этих соотношений вытекает метод измерения ЭДС источника: В режиме короткого замыкания (к.з.) выводы источника соединены между собой, например, сопротивление нагрузки замкнуто проводником с нулевым сопротивлением (рис. 1.19, в). Напряжение на приемнике Он достигает максимально возможного для данного источника (аккумулятора, электрического генератора) и может вызвать, перегрев источника и даже его повреждение. КПД электрической цепи в режиме к.з. — Основные положения, изложенные в п. 1.3 материалов:
Четырехполюсники Четырехполюсник — это устройство, имеющее четыре контакта: два входных контакта, используются для подключения источника сигнала и два выходных — для подключения нагрузки. Четырехполюсники широко применяются в системах передачи информации. Четырехполюсниками являются линии связи в компьютерной сети, телефонные линии, усилители, трансформаторы, фильтры и т.д. Рис. 1.20. Схема четырехполюсника Изображение четырехполюсника с подключенными источником сигнала Четырехполюсник, содержащий линейные элементы, называется линейным. Если внутри четырехполюсника есть нелинейные или параметрические элементы, При анализе удобно рассматривать четырехполюсники в виде "черного ящика", т.е. устройства с некоторой неизвестной для нас внутренней структурой. Внутренняя структура будет проявляться через взаимосвязь входных и выходных токов и напряжений. Рассмотрим уравнения линейных пассивных четырехполюсников. Пусть заданы входной Рис. 1.21. Схема пассивного четырехполюсника
Так как четырехполюсник линейный, то в силу принципа суперпозиции, функции в написанных выше уравнениях будут линейными:
Здесь коэффициенты пропорциональности Полученную систему уравнений можно представить в матричной форме
где Пусть теперь заданы напряжения четырехполюсника:
Коэффициенты Аналогично при заданных
где коэффициент пропорциональности Формулы (1.14, 1.15, 1.16) получены для указанных на рис. 1.20, рис. 1.21 положительных направлений токов и напряжений. При анализе четырехполюсника можно использовать другие положительные направления. Часто вместо тока
Если в уравнениях вместо тока Если введенные выше параметры описывают один и тот же четырехполюсник, то они будут взаимосвязаны. Найдем, например, взаимосвязь между
Здесь Δ — определитель Y -матрицы четырехполюсника. Сравнивая полученные уравнения с формулами (1.14), получим формулы взаимосвязи Z - и Аналогично можно найти формулы взаимосвязи других параметров четырехполюсника друг с другом. Эти формулы можно найти в литературе указанной в конце пособия. Из анализа уравнений четырехполюсника легко получить физический смысл параметров четырехполюсника. Для Z -параметров:
Аналогично для Y -параметров получим: Для уравнений с H -параметрами получим: Z -параметры называются параметрами холостого хода, Y -параметры — параметры короткого замыкания, а H - и остальные параметры — смешанные параметрами. Из названия параметра следует способ его экспериментального определения и расчета аналитическими методами. Как уже отмечалось, четырехполюсник в основном используется в системах передачи сигналов. Для анализа прохождения сигналов через четырехполюсник вводятся функции четырехполюсника. К ним относятся:
Выходное сопротивление равно внутреннему сопротивлению эквивалентного источника напряжения, с помощью которого представляется четырехполюсник Основными и наиболее часто используемыми функциями являются коэффициент передачи по напряжению, входное и выходное сопротивления. Первичные параметры четырехполюсников определяются инвариантно к их внутренней структуре. Однако при реализации конкретных видов четырехполюсника необходимо задаваться их структурой (топологией), при этом обычно их представляют в виде различных Г-, Т-, П-образных и мостовых звеньев сопротивлений (рис. 1.22). Рис. 1.22. Структурные схемы четырехполюсников в виде 5 звеньев цепей: Расчет функций и значений элементов Основные положения, изложенные в п. 1.4 материалов:
Закон Ома. Из (1.5) следует, что падение напряжения на активном резисторе равно произведению величины сопротивления на силу тока протекающего через него:
Откуда сопротивление Величина постоянного напряжения
где:
Из (2.2) следует важный вывод:
Полезная (активная) мощность В ЭЦ рис. 2.1 два элемента потребляют мощность В ЭЦ должен выполняться баланс мощности, физически отражающий закон сохранения энергии. Уравнение баланса:
и для нашего случая В выражении (2.4) составляющие в сумме потребителей мощности имеют только положительные значения и не зависят от знака тока. Составляющие в сумме источников ЭДС Следует учитывать режим работы · направление · направление Пунктиром на рис. 2.1 показан реальный источник ЭДС- Е, отмечающийся Уравнение электрического состояния источника ЭДС будет иметь вид
Аналогичную запись уравнения электрического состояния имеет активная ветвь цепи рис. 2.2, б. Формула 2.5 представляет собой закон Ома для активной ветви ЭЦ. Основные положения, изложенные в п. 2.1 материалов:
2.2. Методы преобразования цепи 2.2.1. Источник, нагруженный на резистор (рис. 2.3) Рис. 2.3. Электрическая цепь под нагрузкой Когда источник питания нагружен активным сопротивлением
откуда
Мощность, выделяемая в сопротивлении
Эта мощность достигает максимума, когда,
и коэффициент полезного действия генератора определится:
Основные характеристики источника, нагруженного на активное сопротивление, Рис. 2.4. Изменение мощности 2.2.2. Закон Кирхгофа Законы Кирхгофа п.1.5 (1.18) и (1.19) запишутся: I Закон Кирхгофа — алгебраическая сумма токов в узле электрической цепи равна нулю
Правило составления уравнений по I закону Кирхгофа — ток, который втекает в узел, имеет положительный знак, который вытекает, отрицательный. Пример для узла Рис. 2.5. Контур электрической цепи II Закон Кирхгофа —в каком-либо контуре ЭЦ алгебраическая сумма электродвижущих сил, действующих в данном контуре, равна алгебраической сумме падений напряжения, в данном контуре:
Правило составления уравнений по II закону Кирхгофа —когда направление обхода контура совпадает с направлением тока в сопротивлении, падение напряжения имеет положительный знак 2.2.3. Последовательное соединение сопротивлений (рис. 2.6) Рис. 2.6. Последовательное соединение В этом случае единственный ток Согласно первому закону Кирхгофа имеем:
откуда
где Для n последовательно включенных сопротивлений будет:
Уравнение баланса мощностей для такой цепи имеет вид:
Последовательное соединение сопротивлений редко используется В схемотехнике последовательное соединение широко используется Правило делителя напряжения: отношение напряжений на элементах последовательной цепи равно отношению сопротивлений этих элементов. Например, для цепи, приведенной на рис. 2.6, по правилу делителя напряжений получим такие выражения для напряжений на ее элементах:
где
2.2.4. Параллельное соединение сопротивлений (рис. 2.7) Единственное напряжение Согласно первому закону Кирхгофа имеем:
откуда
Рис. 2.7. Параллельное соединение Вспомним понятие проводимости (см. п. 1.2), величины обратной сопротивлению
Уравнение баланса мощностей для такой цепи имеет вид:
Частные случаи: 1) Если имеем только два включенных параллельно сопротивления
2) Если имеем несколько одинаковых сопротивлений включенных параллельно, то расчет эквивалентного сопротивления ведем исходя из
откуда для Параллельное соединение сопротивлений широко используется В схемотехнике параллельное соединение широко используется для деления тока. Правило делителя тока: отношение токов в параллельных ветвях равно отношению проводимостей этих ветвей. Для схемы параллельного соединения рис. 2.7 ток
|
|||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.2.239 (0.023 с.) |

 и
и  на рис. 1.18, а).
на рис. 1.18, а).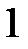 и
и 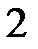 и
и 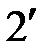 , на рис. 1.18, б).
, на рис. 1.18, б). к суммарной мощности
к суммарной мощности  всех потребителей (элементов), т.к. в ЭЦ имеются потери энергии, например, при нагревании резисторов и т.д.:
всех потребителей (элементов), т.к. в ЭЦ имеются потери энергии, например, при нагревании резисторов и т.д.: (1.13)
(1.13) , номинальный ток —
, номинальный ток — 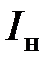 , номинальная мощность —
, номинальная мощность —  , номинальный КПД —
, номинальный КПД —  . Эксплуатация
. Эксплуатация  равно внутреннему сопротивлению источника
равно внутреннему сопротивлению источника 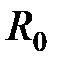 . Согласованный режим характеризуется передачей от данного источника
. Согласованный режим характеризуется передачей от данного источника 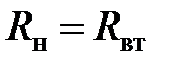 является условием получения этого режима.
является условием получения этого режима.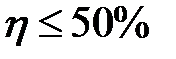 ) и для мощных цепей работа в согласованном режиме экономически невыгодна. Согласованный режим применяется, главным образом, в маломощных цепях, например в устройствах радиоэлектроники, если КПД не имеет существенного значения, а требуется получить в приемнике возможно большую мощность. Так, например: в электронных усилителях мощности в динамик акустических систем требуется создать максимальное акустическое давление; большая мощность требуется в устройствах автоматики для управления электрическими машинами; в микропроцессорной технике и радиотехнике информация по шинам и линиям связи должна передаваться без потерь.
) и для мощных цепей работа в согласованном режиме экономически невыгодна. Согласованный режим применяется, главным образом, в маломощных цепях, например в устройствах радиоэлектроники, если КПД не имеет существенного значения, а требуется получить в приемнике возможно большую мощность. Так, например: в электронных усилителях мощности в динамик акустических систем требуется создать максимальное акустическое давление; большая мощность требуется в устройствах автоматики для управления электрическими машинами; в микропроцессорной технике и радиотехнике информация по шинам и линиям связи должна передаваться без потерь.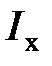 равен нулю. КПД электрической цепи в режиме х.х. —
равен нулю. КПД электрической цепи в режиме х.х. — 
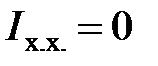 , то падение напряжения на внутренних сопротивлениях источника
, то падение напряжения на внутренних сопротивлениях источника 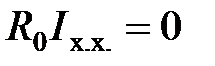 и напряжение на выводах источника
и напряжение на выводах источника 
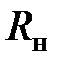 при этом равно нулю. Сопротивление всей ЭЦ внутреннему сопротивлению
при этом равно нулю. Сопротивление всей ЭЦ внутреннему сопротивлению  источника питания,
источника питания, 
 . Для защиты источников электрической и питающих цепей от токов короткого замыкания
. Для защиты источников электрической и питающих цепей от токов короткого замыкания  и выходной
и выходной  токи четырехполюсника (рис. 1.21). Входные и выходные напряжения
токи четырехполюсника (рис. 1.21). Входные и выходные напряжения  и
и  четырехполюсника будут функциями этих токов:
четырехполюсника будут функциями этих токов:

 (1.14)
(1.14) ,
,  ,
,  ,
,  имеют размерность сопротивлений. Соотношения (1.14) называют уравнениями четырехполюсника с Z -параметрами. Сопротивления
имеют размерность сопротивлений. Соотношения (1.14) называют уравнениями четырехполюсника с Z -параметрами. Сопротивления  ,
, 
 характеризуют внутреннюю структуру четырехполюсника. В общем случае
характеризуют внутреннюю структуру четырехполюсника. В общем случае 
 — матрица-столбец заданных токов,
— матрица-столбец заданных токов,  — матрица-столбец напряжений на зажимах четырехполюсника,
— матрица-столбец напряжений на зажимах четырехполюсника,  — матрица сопротивлений четырехполюсника.
— матрица сопротивлений четырехполюсника.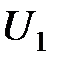 и
и 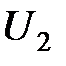 . Заменяя
. Заменяя  (1.15)
(1.15) ,
, 
 в (1.15) имеют размерность проводимостей
в (1.15) имеют размерность проводимостей  -параметрами четырехполюсника, а соотношения — уравнениями четырехполюсника с Y -параметрами.
-параметрами четырехполюсника, а соотношения — уравнениями четырехполюсника с Y -параметрами. и
и  получаем уравнения с H -параметрами:
получаем уравнения с H -параметрами: (1.16)
(1.16) имеет размерность сопротивления,
имеет размерность сопротивления,  — проводимости,
— проводимости,  ,
,  — безразмерные коэффициенты. При заданных
— безразмерные коэффициенты. При заданных 
 получаем уравнения с G -параметрами. Использование в качестве независимых переменных
получаем уравнения с G -параметрами. Использование в качестве независимых переменных  и
и  приводит к уравнениям с В -параметрами.
приводит к уравнениям с В -параметрами. используют ток
используют ток  ,
,  направленный в противоположную сторону. Как правило,
направленный в противоположную сторону. Как правило, вводятся уравнения с А -параметрами:
вводятся уравнения с А -параметрами: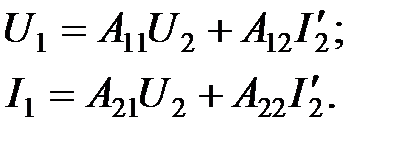 (1.17)
(1.17) использовать ток
использовать ток  , то параметры
, то параметры  и
и 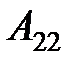 изменят знаки на противоположные.
изменят знаки на противоположные. - и
- и 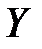 - параметрами. Пусть имеется четырехполюсник, описанный уравнением (1.15)
- параметрами. Пусть имеется четырехполюсник, описанный уравнением (1.15) и
и  ,
,
 ;
;  ;
;  ;
;  .
. — входное сопротивление при холостом ходе на выходе;
— входное сопротивление при холостом ходе на выходе; — сопротивление обратной связи;
— сопротивление обратной связи; — сопротивление прямой передачи;
— сопротивление прямой передачи; — выходное сопротивление при холостом ходе на входе.
— выходное сопротивление при холостом ходе на входе. — входная проводимость
— входная проводимость  — проводимость обратной связи,
— проводимость обратной связи, 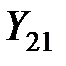 — проводимость прямой передачи,
— проводимость прямой передачи,  — выходная проводимость при котором замыкание на входе.
— выходная проводимость при котором замыкание на входе. — входное сопротивление
— входное сопротивление  — коэффициент обратной связи
— коэффициент обратной связи  — коэффициент прямой передачи по току,
— коэффициент прямой передачи по току,  — выходная проводимость при холостом ходе на входе.
— выходная проводимость при холостом ходе на входе. —коэффициент передачи по напряжению,
—коэффициент передачи по напряжению,  —коэффициент передачи активной мощности,
—коэффициент передачи активной мощности,  — коэффициент передачи по току,
— коэффициент передачи по току, 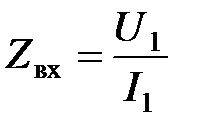 — входное сопротивление,
— входное сопротивление,  — комплексное выходное сопротивление четырехполюсника.
— комплексное выходное сопротивление четырехполюсника.  только при уменьшении до нуля напряжения эквивалентной ЭДС, а этого добиваются уменьшением до нуля напряжения входной ЭДС.
только при уменьшении до нуля напряжения эквивалентной ЭДС, а этого добиваются уменьшением до нуля напряжения входной ЭДС. в схеме замещения производят
в схеме замещения производят 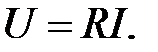 (2.1)
(2.1) , единица измерения которого один Ом.
, единица измерения которого один Ом.  .
. (рис. 2.2, а) определяется:
(рис. 2.2, а) определяется: (2.2)
(2.2) — энергия сторонних сил для переноса единицы заряда
— энергия сторонних сил для переноса единицы заряда  ;
;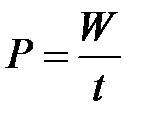 и
и  , соответственно мощность и ток.
, соответственно мощность и ток. —Закон Джоуля-Ленца. (2.3)
—Закон Джоуля-Ленца. (2.3)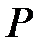 измеряется в ваттах (Вт) и характеризует интенсивность преобразования электрической энергии в тепловую энергию
измеряется в ваттах (Вт) и характеризует интенсивность преобразования электрической энергии в тепловую энергию  , которое в соответствии с п. 1.2 физически отражает способность реальных объектов нагреваться при прохождении постоянного тока, и оценивается в омах (Ом).
, которое в соответствии с п. 1.2 физически отражает способность реальных объектов нагреваться при прохождении постоянного тока, и оценивается в омах (Ом). соответственно
соответственно  и
и  , а один источник энергии с мощностью
, а один источник энергии с мощностью  .
. (2.4)
(2.4) .
. имеют разные знаки в зависимости от режима работы источника энергии.
имеют разные знаки в зависимости от режима работы источника энергии. (рис. 2.1, рис. 2.2) в зависимости:
(рис. 2.1, рис. 2.2) в зависимости: (рис. 2.1) совпадают — источник ЭДС работает в режиме источника энергии и в сумме (2.4) берется знак «+».
(рис. 2.1) совпадают — источник ЭДС работает в режиме источника энергии и в сумме (2.4) берется знак «+». (2.4) берется со знаком «–».
(2.4) берется со знаком «–». и отражающего потери энергии (обычно в виде тепла).
и отражающего потери энергии (обычно в виде тепла). (2.5)
(2.5)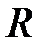 , уравнение электрического состояния ЭЦ запишется:
, уравнение электрического состояния ЭЦ запишется: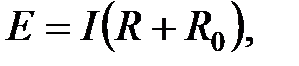

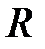 :
:
 (согласованный режим работы ЭЦ см. п.1.3), то есть
(согласованный режим работы ЭЦ см. п.1.3), то есть
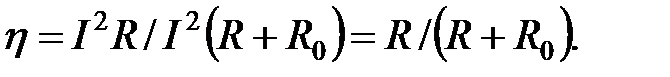
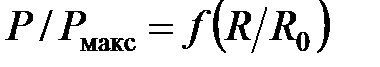 и
и  представлены на рис. 2.4.
представлены на рис. 2.4. и КПД от нагрузки
и КПД от нагрузки 
 (2.6)
(2.6) рис. 2.5:
рис. 2.5:  .
. (2.7)
(2.7) , в тоже время имеет отрицательный знак
, в тоже время имеет отрицательный знак  , если направления не совпадают. Когда направление обхода контура совпадает с направлением ЭДС, имеем положительный знак
, если направления не совпадают. Когда направление обхода контура совпадает с направлением ЭДС, имеем положительный знак  , однако имеем отрицательный знак
, однако имеем отрицательный знак  , если направления не совпадают.
, если направления не совпадают.  рис. 2.5:
рис. 2.5: 

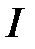 течет через все сопротивления
течет через все сопротивления  .
.
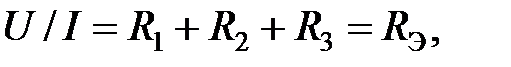
 — эквивалентное сопротивление.
— эквивалентное сопротивление. (2.8)
(2.8)



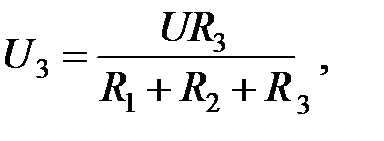
 — общий ток через все сопротивления.
— общий ток через все сопротивления. приложено ко всем сопротивлениям
приложено ко всем сопротивлениям  .
.

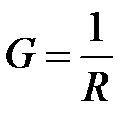 . Тогда для
. Тогда для  включенных параллельно сопротивлений будет:
включенных параллельно сопротивлений будет: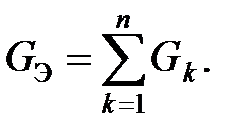 (2.9)
(2.9)
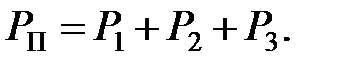
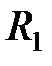 и
и 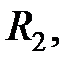 то расчет эквивалентного сопротивления ведем исходя из
то расчет эквивалентного сопротивления ведем исходя из 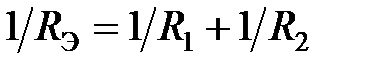 , откуда
, откуда (2.10)
(2.10)
 сопротивлений
сопротивлений  . (2.11)
. (2.11)
 -ой ветви по закону Ома равен
-ой ветви по закону Ома равен  тогда, для двух параллельных сопротивлений (частн
тогда, для двух параллельных сопротивлений (частн 


