
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитические методы анализа нелинейных электрических цепейСодержание книги
Поиск на нашем сайте Графические методы анализа НЭЦ наглядны, но они носят индивидуальный характер, т.е. не позволяют проводить обобщенный анализ НЭЦ при произвольных нелинейных элементах и видах воздействий. Аналитические методы свободны от этого недостатка, но требуют аналитической аппроксимации ВАХ НЭ. Наиболее часто используются два вида аппроксимации ВАХ НЭ: • полиномиальная; • кусочно-линейная. При полиноминальной аппроксимации ВАХ НЭ аппроксимируется полиномом вида
Коэффициенты аппроксимирующего полинома могут быть определены путем решения системы уравнений, полученной из ВAX НЭ. Пример 2.13. Для полинома
Из этих уравнений находим значения При кусочно-линейной аппроксимации ВАХ НЭ аппроксимируется совокупностью линейных участков (кусков) вблизи возможных рабочих точек. Рис. 2.40. ВАХ при полиноминальной аппроксимации Пример 2.14. Для двух участков нелинейной ВАХ (рис. 2.41) получим:
Рис. 2.41. ВАХ при кусочно-линейной аппроксимации Пример 2.15. Пусть требуется линеаризировать участок ВАХ между точками Рис. 2.42. ВАХ к примеру 2.15 Участок
Тогда уравнение линеаризированного участка ВАХ вблизи рабочей
Очевидно, что аналитическая аппроксимация ВАХ верна только Пример 2.16. На рис. 2.43 представлена схема соединения НЭ, ВАХ которых заданы аналитически: для НЭ1: для НЭ2: Рис. 2.43. Схема к примеру 2.16 Определить в аналитической форме зависимость Решение. При последовательном соединении НЭ выполняются условия
Решаем совместно уравнения (2.27) и (2.28),
которое с учетом (2.29) примет вид квадратичного уравнения:
или
Решение последнего уравнения:
Из (2.28) найдем искомый ток в схеме
Пример 2.17. Имеется схема стабилизации напряжения рис. 2.44. Рис. 2.44. Схема к примеру 2.17 Определить в аналитическом виде зависимость отношения Рис. 2.45. ВАХ стабилитрона Решение. Воспользоваться методом линеаризации. В режиме стабилизации напряжения стабилитрон работает на линейном участке его ВАХ: (рис. 2.45), Рис. 2.46. Эквивалентная схема стабилитрона Для схемы рис. 2.46 справедливо уравнение Так как в схеме стабилизации напряжения выполняется неравенство Коэффициент стабилизации напряжения в схеме рис. 2.44 возрастает Основные положения, изложенные в п. 2.5 материалов:
2.6. Вопросы и задания для самопроверки 1. В чем заключается задача анализа цепи? 2. Как рассчитываются линейные резистивные цепи с одним источником постоянного действия? 3. Найти показания амперметра в цепи, изображенной на рис. 2.47, а, 4. Как преобразовать соединение сопротивлений звездой в соединение треугольником наоборот? 5. Сформулируйте законы Кирхгофа и Ома. 6. Используя законы Ома и Кирхгофа, определить показания вольтметра Рис. 2.47. Схемы к заданиям 3 (а) и 6 (б) самоконтроля 7. Объясните, в чем состоит сущность метода наложения. Каков порядок расчета линейных резистивных цепей методом наложения? 8. В чем суть расчета цепей методом непосредственного изменения законов Кирхгофа? 9. Каков порядок расчета цепи методом контурных токов? 10. Каков порядок расчета цепи методом узловых напряжений (потенциалов)? 11. При помощи законов Кирхгофа рассчитайте токи в ветвях цепи Рис. 2.48. Схема к заданию 11 Рис. 2.49. Схема к заданию 5 12. Для схемы рис. 2.49 определите число уравнений, которые необходимо составить по первому и второму законам Кирхгофа, и запишите эти уравнения. Указание: точки, соединенные на схеме проводником, считайте одним узлом, вольтметр — идеальным (т.е. имеющим бесконечно большое сопротивление), поэтому при составлении уравнений его можно не принимать во внимание. 13. В схеме рис. 2.49 определите показания вольтметра. Указание: вольтметр измеряет напряжение между точками, к которым 14. Поясните, чем отличается метод контурных токов от метода непосредственного применения законов Кирхгофа. 15. Для схемы рис. 2.49 составьте уравнение по методу контурных токов. 16. Для схемы рис. 2.49 составьте уравнение по методу узловых напряжений (потенциалов). 17. Сделайте вывод каким методом по п.п. 15, 16 предпочтительнее (легче) расчитать схему рис. 2.49?
|
|||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.2.239 (0.008 с.) |


 по заданной ВАХ НЭ
по заданной ВАХ НЭ и два уравнения:
и два уравнения:

 и
и  .
. — крутизна первого участка линеаризации,
— крутизна первого участка линеаризации, — крутизна второго участка линеаризации.
— крутизна второго участка линеаризации. и
и  , который используется в качестве рабочей области около рабочей
, который используется в качестве рабочей области около рабочей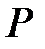 (рис. 2.42).
(рис. 2.42). ВАХ НЭ заменяем "куском" прямой линии с крутизной
ВАХ НЭ заменяем "куском" прямой линии с крутизной
 будет:
будет:
 (2.27)
(2.27) (2.28)
(2.28) , если считать напряжение
, если считать напряжение  на входе схемы рис. 2.43 заданной величиной.
на входе схемы рис. 2.43 заданной величиной.
 (2.29)
(2.29)



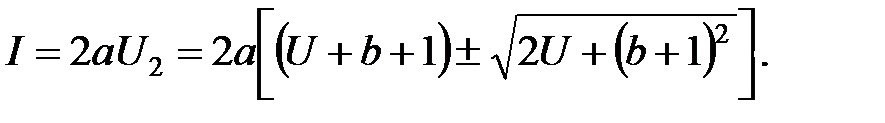
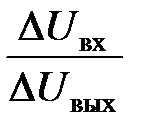 (коэффициент стабилизации напряжения) от параметров балансного резистора
(коэффициент стабилизации напряжения) от параметров балансного резистора 
 .
. и
и  схемы определяется графически
схемы определяется графически  так как
так как  можно записать
можно записать  . Продифференцировав полученное выражение по выходному напряжению, находим
. Продифференцировав полученное выражение по выходному напряжению, находим  .
. , окончательно имеем
, окончательно имеем  .
.


 Сопротивление амперметра
Сопротивление амперметра 
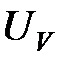
 и всех сопротивлений приведены в задании 3.
и всех сопротивлений приведены в задании 3.







