
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет линейных цепей при несинусоидальных напряжениях и токахСодержание книги
Поиск на нашем сайте
Для расчета режима линейной цепи периодического несинусоидального тока (цепи, у которой параметры элементов R, L, C не зависят от тока и напряжения) применим метод наложения (см. 2.3.3): каждую из гармонических составляющих В качестве примера рассмотрим расчет тока в цепи по рис. 4.2
Ток в этой цепи
где по закону Ома для первой гармоники
При определении каждой из гармонических составляющих можно применять любые методы расчета цепей синусоидального тока, в том числе и символический (комплексный). На практике для выбора и оценки различных электротехнических устройств, при расчетах и измерениях в электрических цепях с периодически изменяющимися токами и напряжениями любой формы в качестве одной из основных характеристик пользуются действующим значением.Действующее значение любой периодической функции, как в частном случае и синусоидальной (см. п.3.1.2) — это среднеквадратичное значение, например, действующие значения несинусоидальных токов, напряжений и ЭДС
или учитывая (4.1) можно показать
Таким образом, действующее значение периодического несинусоидального тока (напряжения, ЭДС) равно корню квадратному из суммы квадратов постоянной составляющей Так же определяется действующее значение периодического несинусоидального напряжения:
Действующее значение несинусоидальной величины может быть измерено при помощи электроизмерительных приборов электромагнитной, электродинамической, тепловой и других систем (см. гл. 10). Важной характеристикой цепей несинусоидального тока является мощность. Активная мощность
После подстановки в (4.6) напряжения (4.5) и тока (4.4) в виде рядов активной мощности будем иметь
т.е. активная мощность периодического несинусоидального тока равна сумме активных мощностей всех гармонических составляющих и мощности постоянных составляющих напряжения и тока (мощности постоянного тока). Реактивной мощностью периодических несинусоидальных токов можно условно считать величину
Полная мощность цепи несинусоидального тока равна произведению действующих значений несинусоидальных напряжений и тока, т.е.
Методика расчета линейных цепей при несинусоидальных напряжениях Производится наложение мгновенных значений токов (напряжений) всех учитываемых гармонических составляющих и постоянной составляющей. Определяются действующие значения мощность по вышеприведенным выражениям. Для постоянной составляющей рассчитывается цепь постоянного тока методами, рассмотренными в гл. 2. При этом учитывается, что индуктивное сопротивление При расчете отдельных гармонических составляющих с частотами Пример 4.1. На входе цепи (рис. 4.3) периодическое несинусоидальное напряжение Рис. 4.3. Схема к примеру 4.1 Решение. Токи определим методом наложения (цифровой индекс у всех величин — номер гармоники). На схеме показаны выбранные положительные направления токов. Постоянная составляющая тока Суммарное комплексное сопротивление для первой гармоники тока
Ток первой гармоники в неразветвленной части цепи
Напряжение первой гармоники на участке ab
Токи первой гармоники в параллельных ветвях:
Общее комплексное сопротивление для третьей гармоники тока
где Напряжение третьей гармоники на участке ab
Токи третьей гармоники в параллельных ветвях:
Мгновенные значения токов:
Действующие значение токов (показания амперметров):
Активная мощность цепи
Полная мощность
Пример 4.2. Катушка с активным сопротивлением Записать выражение для мгновенного тока и составить баланс активной мощности цепи, если частота основной гармоники а) б) в) г) Рис. 4.4. Схема замещения к примеру 4.2 Решение. На рис. 4.4, а изображена схема замещения рассматриваемой цепи,
Постоянная составляющая и амплитудные значения гармоник тока
Действующие значения гармонических составляющих ЭДС и тока:
Активная мощность источников энергии
Активная мощность приемника электроэнергии
Баланс мощностей:
4.1.2. Электрические фильтры При воздействии несинусоидального напряжения на индуктивный элемент L высшие гармонические составляющие тока в элементе подавляются, причем чем выше номер гармоники, тем сильнее, так как
Для емкостного элемента, наоборот, высшие гармонические составляющие тока усиливаются, так как
В цепях несинусоидального периодического тока возможны резонансы напряжений или токов при частотах отдельных гармоник. Условия возникновения На зависимости индуктивных и емкостных сопротивлений от частоты основан принцип работы электрических фильтров — устройств, с помощью которых гармонические составляющие токов и напряжений определенной частоты Сглаживающие фильтры. Сглаживающие фильтры служат для уменьшения процентного содержания на сопротивлении нагрузки гармонических составляющих выпрямленного напряжения или снижения процентного содержания высших гармоник в кривой переменного напряжения. Рассмотрим работу простейшего сглаживающего фильтра (рис. 4.5) представляющего собой пассивный линейный четырехполюсник, к выходным выводам которого подключен приемник с сопротивлением нагрузки
а) б) Рис. 4.5. RC-сглаживающий фильтр (а) и его АЧХ (б)
Соответствующая амплитудно-частотная характеристика фильтра
приведена на рис. 4.5, б. Чем выше частота гармоники напряжения на входе Резонансные фильтры. В резонансных фильтрах используются явления резонансов напряжений и токов в электрических цепях (см. пп. 3.3.5, 3.3.6) На рис. 4.8, а приведена схема простейшею полосового фильтра
а) б) Рис. 4.8. Схема резонансного фильтра (а) и его АЧХ (б)
а) б) Рис. 4.9. Схема заградительного фильтра (а) и его АЧХ (б) Ширина полосы частот В заградительном фильтре по схеме на рис. 4.9, а используется
приведена на рис. 4.9, б. Ширина полосы частот Комбинации явлений резонансов напряжений и токов в различных ветвях фильтра позволяют создавать полосовые и заградительные фильтры высокого качества. Избирательные RС-фильтры. Фильтры, содержащие только резисторы
где
а) б) Рис. 4.10. Схема фильтра с мостом Вина (а), его АЧХ и ФЧХ(б) Рис. 4.11. Схема фильтра с двойным Т-образным мостом Амплитудно-частотная
При этом фазочастотная характеристика равна нулю. Заградительный RС-фильтр можно реализовать с помощью двойного Возможны и другие схемотехнические решения избирательных Основные положения, изложенные в п. 4.1 материалов
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 579; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.21.101 (0.008 с.) |



 , для пятой гармоники
, для пятой гармоники  и используя (3.31) найдем фазовый сдвиг
и используя (3.31) найдем фазовый сдвиг  :
: ;
;  .
. (4.3)
(4.3) (4.4)
(4.4) и квадратов действующих значений всех гармонических составляющих
и квадратов действующих значений всех гармонических составляющих  , где k = 1, 2... Следует обратить внимание на то, что действующее значение несинусоидальных периодических величин не зависят от начальных фаз гармонических составляющих
, где k = 1, 2... Следует обратить внимание на то, что действующее значение несинусоидальных периодических величин не зависят от начальных фаз гармонических составляющих 
 (4.5)
(4.5) цепи несинусоидального тока определяется так же,
цепи несинусоидального тока определяется так же,  ) за период.
) за период. (4.6)
(4.6) (4.7)
(4.7) (4.8)
(4.8) (4.9)
(4.9) , а емкостное
, а емкостное  бесконечно велико (для постоянной составляющей
бесконечно велико (для постоянной составляющей  ). Следовательно, нужно участок с индуктивным элементом закоротить, а с емкостным — отключить.
). Следовательно, нужно участок с индуктивным элементом закоротить, а с емкостным — отключить. можно пользоваться символическим (комплексным) методом учитывая, что сопротивления реактивных элементов цепи для отдельных гармоник будут различными. Для k -й гармонической составляющей с частотой
можно пользоваться символическим (комплексным) методом учитывая, что сопротивления реактивных элементов цепи для отдельных гармоник будут различными. Для k -й гармонической составляющей с частотой  индуктивное сопротивлении
индуктивное сопротивлении  , а емкостное
, а емкостное  , т.е. с ростом порядка гармоники и угловой частоты
, т.е. с ростом порядка гармоники и угловой частоты  индуктивное сопротивление увеличивается в k раз, а емкостное уменьшается в k раз по сравнению
индуктивное сопротивление увеличивается в k раз, а емкостное уменьшается в k раз по сравнению  Активное сопротивление, если нет дополнительных указаний, можно считать
Активное сопротивление, если нет дополнительных указаний, можно считать ).
). Активное сопротивление
Активное сопротивление  При основании частоте
При основании частоте  индуктивное сопротивление
индуктивное сопротивление  , емкостное
, емкостное  Определить мгновенные значения всех токов, активную и полную мощности, показания амперметров, измеряющих действующее значение токов.
Определить мгновенные значения всех токов, активную и полную мощности, показания амперметров, измеряющих действующее значение токов. отсутствует в ветви с конденсатором. Поэтому по закону Ома
отсутствует в ветви с конденсатором. Поэтому по закону Ома  А (здесь учтено, что для постоянной составляющей индуктивное сопротивление равно нулю).
А (здесь учтено, что для постоянной составляющей индуктивное сопротивление равно нулю). Ом.
Ом. A.
A. В.
В. A;
A; A.
A. ,
, Ом;
Ом; 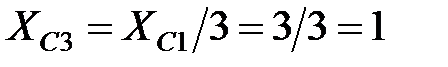 Ом, т.е.
Ом, т.е. 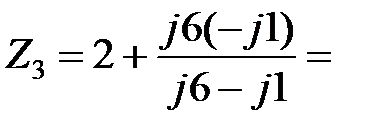
 Ом.
Ом. B.
B.
 A;
A; A.
A.


 A;
A;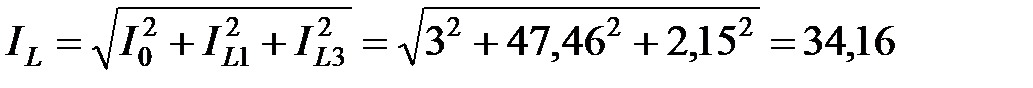 A;
A; A.
A.
 ВА.
ВА.
 подключена к источнику питания, ЭДС которого изменяется по несинусоидальному закону
подключена к источнику питания, ЭДС которого изменяется по несинусоидальному закону  B.
B. .
. ), сопротивление определяется только резистивным элементом
), сопротивление определяется только резистивным элементом  , сопротивление индуктивного элемента
, сопротивление индуктивного элемента  равно нулю. Комплексные сопротивления частичных схем:
равно нулю. Комплексные сопротивления частичных схем: Ом;
Ом; Ом;
Ом;  ;
; Ом;
Ом; Ом;
Ом;  ;
; A;
A;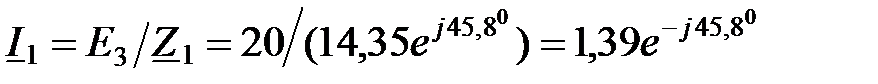 A;
A; A;
A; B;
B;  B.
B. A;
A;  A.
A.
 Вт.
Вт. ; 20,4 Вт
; 20,4 Вт  20,3 Вт
20,3 Вт .
.
 , а резонанс токов при
, а резонанс токов при  , где k — номер гармоники. В режиме резонанса угол сдвига фаз
, где k — номер гармоники. В режиме резонанса угол сдвига фаз  между напряжением и током контура при частоте этой гармоники равен нулю, напряжения (или токи) на отдельных участках цепи могут резко возрастать и быть больше, чем общее напряжение или ток контура.
между напряжением и током контура при частоте этой гармоники равен нулю, напряжения (или токи) на отдельных участках цепи могут резко возрастать и быть больше, чем общее напряжение или ток контура.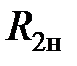 . Коэффициент передачи напряжения фильтра, цепь которого вместе
. Коэффициент передачи напряжения фильтра, цепь которого вместе  .
.
 фильтра, тем меньше ее процентное содержание в напряжении на его выходе
фильтра, тем меньше ее процентное содержание в напряжении на его выходе  (рис. 4.6). Аналогичными свойствами обладает сглаживающий фильтр по схеме
(рис. 4.6). Аналогичными свойствами обладает сглаживающий фильтр по схеме  .
. , выделяемая фильтром, на уровне
, выделяемая фильтром, на уровне  тем меньше, чем больше добротность цепи
тем меньше, чем больше добротность цепи 
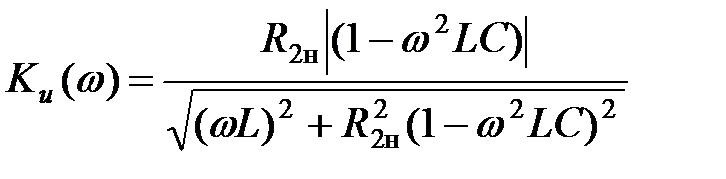
 , заграждаемых
, заграждаемых .
. (4.10)
(4.10) и
и  — комплексные сопротивления.
— комплексные сопротивления. и фазочастотная
и фазочастотная  характеристики моста Вина приведены на рис. 4.10, б. Максимальное значение амплитудно-частотной характеристики равно
характеристики моста Вина приведены на рис. 4.10, б. Максимальное значение амплитудно-частотной характеристики равно  и достигается при угловой частоте
и достигается при угловой частоте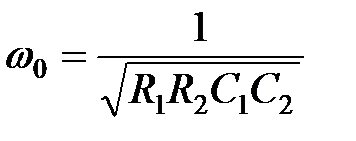 . (4.11)
. (4.11) . Доказательство этого условия достаточно трудоемкое и здесь не приводится.
. Доказательство этого условия достаточно трудоемкое и здесь не приводится.


