
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод двух узлов (частный случай метода узловых напряжений)Содержание книги
Поиск на нашем сайте
Этот метод применяется для расчета электрических цепей с двумя узлами, между которыми включены активные и пассивные ветви (рис. 2.19). Идея метода состоит в том, что по расчетной формуле определяется напряжение между узлами, называемое узловым напряжением Рис. 2.19. Схема параллельного соединения Выведем формулу для расчета узлового напряжения. Положительные направления токов в ветвях выберем от узла
Запишем первый закон Кирхгофа для узла
или
Напряжение между узлами
или в общем виде
Если ЭДС направлена к узлу, обозначенному первым индексом (а), Пример 2.6. Решить пример 2.3 методом двух узлов. Решение. Рассчитаем проводимость ветвей (см. рис. 2.16).
Узловое напряжение
Токи в ветвях:
2.3.8. Метод эквивалентного генератора (активного двухполюсника) Метод эквивалентного генератора дает возможность часть сложной электрической цепи с источниками энергии и двумя выделенными выводами, Рис. 2.20. Активный двухполюсник Доказательство метода. В сложной электрической цепи (рис. 2.20 а), показанной в виде активного двухполюсника A с выделенным участком, сопротивление которого
В соответствии с принципом наложения схему рис. 2.20, б можно представить в виде двух вспомогательных схем, в одной из которых действует источник ЭДС По принципу суперпозиции (наложения) (см. п. 1.5.1) ток
где Порядок расчета. Для расчета тока в сопротивлении Пример 2.7. Для схемы по рис. 2.21 заданы ЭДС и сопротивления: Рис. 2.21. Схема к примеру 2.7 Решение. В соответствие с порядком расчета отключим сопротивление
Входное сопротивление между выводами Ток
В заключении отметим, что все рассмотренные методы расчета цепей постоянного тока применимы к цепям с изменяющимся во времени токами, и будут широко использоваться в главах 3, 4 и т.д. Основные положения, изложенные в п. 2.3 материалов.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.153.251 (0.007 с.) |

 , а затем по закону Ома рассчитываются токи в ветвях.
, а затем по закону Ома рассчитываются токи в ветвях. к узлу
к узлу  . Напряжение
. Напряжение 

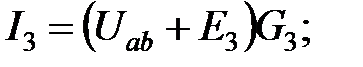

 . Подставляя значение токов
. Подставляя значение токов 


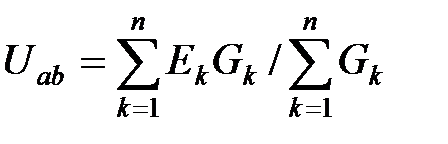 (2.21)
(2.21) записывается со знаком плюс, если от узла — со знаком минус независимо от положительных направлений токов. Если в ветви нет ЭДС,
записывается со знаком плюс, если от узла — со знаком минус независимо от положительных направлений токов. Если в ветви нет ЭДС,  . Методом двух узлов легко решаются любые схемы
. Методом двух узлов легко решаются любые схемы 


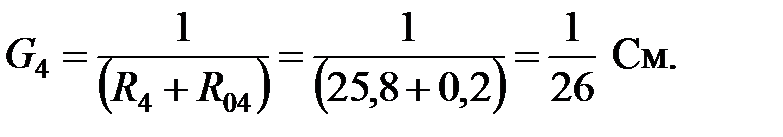





 , то можно найти ток
, то можно найти ток  в этом сопротивлении. Поэтому метод эквивалентного генератора рационально применять, если необходимо найти ток в одной ветви сложной электрической цепи, не рассчитывая токи в других ветвях.
в этом сопротивлении. Поэтому метод эквивалентного генератора рационально применять, если необходимо найти ток в одной ветви сложной электрической цепи, не рассчитывая токи в других ветвях. , требуется найти ток
, требуется найти ток  . Включим последовательно
. Включим последовательно 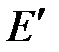 и
и 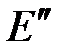 (рис. 2.20, б), с напряжениями, равными напряжению между выводами
(рис. 2.20, б), с напряжениями, равными напряжению между выводами 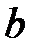 активного двухполюсника
активного двухполюсника  ,
, . Так как
. Так как  ,то вспомогательной схеме рис. 2.20, в частичный ток
,то вспомогательной схеме рис. 2.20, в частичный ток  равен нулю, что следует из закона Ома:
равен нулю, что следует из закона Ома:  , следовательно, частичный ток
, следовательно, частичный ток  (рис. 2.20, г) равен искомому
(рис. 2.20, г) равен искомому (2.22)
(2.22) — внутреннее или входное сопротивление пассивного двухполюсника,
— внутреннее или входное сопротивление пассивного двухполюсника,  и
и  . Ток
. Ток 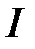
 следует сначала отключить это сопротивление и определить напряжение
следует сначала отключить это сопротивление и определить напряжение  на его выводах.
на его выводах. 



 Найти ток
Найти ток  в ветви
в ветви  .
.
 (рис. 2.21, б) по 2.21:
(рис. 2.21, б) по 2.21:
 при исключенных ЭДС
при исключенных ЭДС 
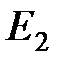 (рис. 2.21, в),
(рис. 2.21, в), 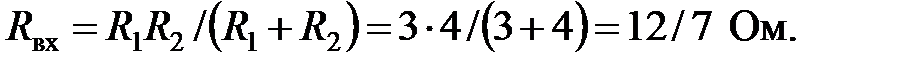 (сопротивление
(сопротивление 
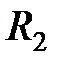 включены параллельно).
включены параллельно).



