Цепь синусоидального тока с последовательно соединенными активным и реактивным сопротивлениями
Рассмотрим схемы последовательного соединения и порядок их расчета.

Рис. 3.21. Схема последовательного соединения RL элементов
Запишем  -ой закон Кирхгофа для RL -цепи рис.3.21: -ой закон Кирхгофа для RL -цепи рис.3.21:

Последнее выражение представляет собой закон Ома RL -цепи.
Определим  — полное комплексное сопротивление равное — полное комплексное сопротивление равное
 , ,
где
·  , (3.28) , (3.28)
·  , (3.29) , (3.29)
·  . .
Векторная диаграмма RL -цепи для случая  приведена на рис. 3.22. приведена на рис. 3.22.

Рис. 3.22. Векторная диаграмма RL -цепи

Рис. 3.23. Схема последовательного соединения RC элементов
Запишем  -ой закон Кирхгофа RC -цепи рис. 3.22: -ой закон Кирхгофа RC -цепи рис. 3.22:

Последнее выражение представляет собой закон Ома для RC -цепи.
Определим  — полное комплексное сопротивление равное — полное комплексное сопротивление равное
 , ,
где
·  , (3.30) , (3.30)
·  , (3.31) , (3.31)
·  . .
Векторная диаграмма RC -цепи для случая  приведена на рис. 3.24. приведена на рис. 3.24.

Рис. 3.24. Векторная диаграмма RC -цепи
Векторные диаграммы последовательных цепей представлены на рис. 3.22
и рис. 3.24. Видно, что меняя выражениях (3.29) и (3.31) соотношение величин активных и реактивных элементов можно управлять углом  сдвига фаз между напряжением и током, в пределах указанных выше. Сопротивление сдвига фаз между напряжением и током, в пределах указанных выше. Сопротивление  в RL цепи имеет характер активно-индуктивный (это значит, что в цепи используется преимущественно тепловая и электромагнитная энергия). Сопротивление в RL цепи имеет характер активно-индуктивный (это значит, что в цепи используется преимущественно тепловая и электромагнитная энергия). Сопротивление  в RC цепи имеет характер активно-емкостной (это значит, что в цепи используется преимущественно тепловая и электростатическая энергия). в RC цепи имеет характер активно-емкостной (это значит, что в цепи используется преимущественно тепловая и электростатическая энергия).

| 
| | а)
| б)
| Рис. 3.25. Электрическая цепь (а) и векторная диаграмма (б) RL -цепи
Пример 3.10. В сеть синусоидального напряжения частотой 50 Гц
включена катушка индуктивности с параметрами L, R (рис. 2.25, а).
Приборы, измеряющие действующие значения напряжения и тока, включенные
в цепь, показывают:  В, В,  А. Активное сопротивление катушки А. Активное сопротивление катушки
 Ом. Определить индуктивность катушки, угол сдвига фаз между напряжением и током, построить векторную диаграмму. Ом. Определить индуктивность катушки, угол сдвига фаз между напряжением и током, построить векторную диаграмму.
Решение. Полное сопротивление катушки  Ом. Ом.
Из формулы (3.28) и (3.29) следует, что
 Ом; Ом;

Так как частота сети  Гц, то Гц, то  мГн. Напряжения: мГн. Напряжения:  B; B;  B. B.
Для построения векторной диаграммы выберем равной нулю начальную фазу тока. Построим в выбранном масштабе пи вектор тока. Вектор  совпадает по фазе с вектором совпадает по фазе с вектором  , а вектор , а вектор  опережает его по фазе на угол 90°. опережает его по фазе на угол 90°.
Вектор напряжения цепи  (рис. 2.25, б). (рис. 2.25, б).
При построении векторов напряжений выбран масштаб  . .

| 
| | а)
| б)
| Рис. 3.26. Электрическая цепи (а) и векторная диаграмма (б)
Пример 3.11. В сеть с частотой 100 Гц включены резистор с сопротивлением  Ом и конденсатор емкостью Ом и конденсатор емкостью  мкФ (рис. 3.26, а). мкФ (рис. 3.26, а).
Определить мгновенное значение напряжения сети, построить векторную диаграмму, если действующее значение тока  A. A.
Решение. Используя (3.30) и (3.31) находим комплексное сопротивление цепи
 Ом. Ом.
Напряжение сети  В (начальная фаза тока В (начальная фаза тока  принята равной нулю). Переходя от комплексного выражения к мгновенному значению, получаем: принята равной нулю). Переходя от комплексного выражения к мгновенному значению, получаем:  B. B.
Для построения векторной диаграммы выбираем масштабы  и и  Строим векторы напряжений в соответствии с расчетом (рис. 2.36, б). Строим векторы напряжений в соответствии с расчетом (рис. 2.36, б).
 В; В;  B. B.
Угол сдвига фаз  равен аргументу комплексного сопротивления, равен аргументу комплексного сопротивления,
т.е. 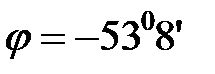 . .
3.3.5. Цепь переменного синусоидального тока с последовательно соединенными элементами R, L, C

Рис. 3.27. Электрическая цепь с последовательно соединенным  элементами элементами
На практике электрическую цепь можно представить как последовательное соединение трех идеальных элементов: сопротивление,индуктивность и емкость.
Запись 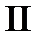 -го закона Кирхгофа для этой цепи дает следующее уравнение -го закона Кирхгофа для этой цепи дает следующее уравнение
в комплексной форме с действующими значениями
 (3.32) (3.32)
или
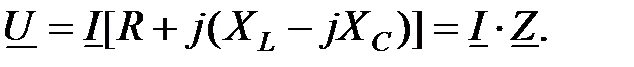 (3.33) (3.33)
Выражение (3.33) является законом Ома для последовательной  цепи, а цепи, а  — полным комплексным сопротивлением — полным комплексным сопротивлением  цепи. цепи.
 , (3.34) , (3.34)
где
 , (3.35) , (3.35)
 (3.36) (3.36)
Анализируя полученные формулы (3.32) и (3.36) можно констатировать,
что все представленные величины зависят от разности  . .
В результате появляются три соотношения:   
Рассмотрим их по порядку.
Рис. 3.28. Векторные диаграммы  цепи: (а) цепи: (а)  ; (б) ; (б)  ; ;
(в) 
1. 
В этом случае  , и из выражений (3.32) - (3.36) следует: , и из выражений (3.32) - (3.36) следует:
 ; ;  ; ;  — сопротивления цепи имеет — сопротивления цепи имеет
активно-индуктивный характер. Векторная диаграмма цепи показана на рис. 3.28, а. Фазовым углом  можно управлять, изменяя соотношение можно управлять, изменяя соотношение  сопротивлений (3.36) в пределах сопротивлений (3.36) в пределах  . .
2. 
В этом случае  , и из выражений (3.32) - (3.36) следует: , и из выражений (3.32) - (3.36) следует:
 ; ;  ; ;  — сопротивление цепи имеет активно-емкостной характер. Векторная диаграмма цепи показана на рис. 3.28, б. Фазовым углом — сопротивление цепи имеет активно-емкостной характер. Векторная диаграмма цепи показана на рис. 3.28, б. Фазовым углом  можно управлять в пределах можно управлять в пределах 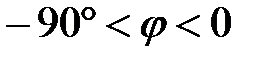 , изменяя соотношения , изменяя соотношения  сопротивлений (3.36). сопротивлений (3.36).

| 
| | а)
| б)
| Рис. 3.29. Временные графики тока и напряжения для векторных диаграмм
рис. 3.28, (а) и рис. 3.28, (б)
Временные графики тока и напряжения, соответствующие соотношениям  и и  изображены на рис. 3.29. Они также отражают изображены на рис. 3.29. Они также отражают
и соответствуют результатам анализа диаграмм рис. 3.28, а и рис. 3.28, б.
3. 
В этом случае выполняется равенство
 (3.37) (3.37)
Из соотношений (3.32) - (3.36) следует:
 ; ;  ; ;  . .  — сопротивление в цепи имеет чисто активный характер. Векторная диаграмма цепи изображена на рис. 3.28, в, — сопротивление в цепи имеет чисто активный характер. Векторная диаграмма цепи изображена на рис. 3.28, в,
и соответствует временным графикам тока и напряжения рис. 3.13, б.
Этот режим работы цепи получил название резонанс напряжений. Он реализуется при выполнении условия резонанса (3.37), при котором  , ( , ( , ,  . Признаком выполнения режима резонанса напряжения является наличие максимального значения тока в цепи . Признаком выполнения режима резонанса напряжения является наличие максимального значения тока в цепи  при достижении при достижении
емкости  значения, как это показано на рис. 3.30. значения, как это показано на рис. 3.30.
Из соотношения для резонанса напряжения (3.37) можно вывести формулу для резонансной частоты 
 . .
Из этого выражения следует, что режим резонанса можно получить тремя способами: изменениями частоты  , индивидуальности , индивидуальности  или емкости или емкости  (рис. 3.30). Однако в любом случае явления в цепи при резонансе одинаковые. (рис. 3.30). Однако в любом случае явления в цепи при резонансе одинаковые.

| 
| | Рис. 3.30. График изменения тока цепи
| Рис. 3.31. Векторная диаграмма при резонансе напряжений
| Сопротивление реактивного элемента при резонансной частоте называется характеристическим сопротивлением последовательного контура
 (3.38) (3.38)
Отношение характеристического сопротивления к активному сопротивлению контура называется добротностью последовательного контура
 (3.39) (3.39)
Рассмотрим характерные особенности режима резонанса напряжений:
1. Так как  , то , то  и суммарное сопротивление участка цепи активное, т.е. полное сопротивление при резонансе равно активному сопротивлению и суммарное сопротивление участка цепи активное, т.е. полное сопротивление при резонансе равно активному сопротивлению

и минимально при заданном R.
2. Ток  максимален максимален  . Это свойство позволяет обнаружить резонанс напряжений при изменении . Это свойство позволяет обнаружить резонанс напряжений при изменении   или С. Однако резонансный ток при определенных условиях опасен — он может привести к перегреву элементов цепи и выводу их из строя. или С. Однако резонансный ток при определенных условиях опасен — он может привести к перегреву элементов цепи и выводу их из строя.
3. Напряжения на отдельных участках контура:
 ; ;  ; ;  . .
Так как при резонансе  , то напряжения на участках контура , то напряжения на участках контура
с реактивными элементами равны (  ), напряжение на участке с активным элементом ), напряжение на участке с активным элементом  равно напряжению питания на выводах контура и совпадает c ним равно напряжению питания на выводах контура и совпадает c ним
по фазе:

Если  , то , то  , т.e. напряжение на участках , т.e. напряжение на участках
с реактивными элементами может быть больше, чем напряжение питания
(см. рис. 3.31). Это свойство— усиление напряжения — является важнейшей особенностью резонанса напряжений и широко используется в технике, отсюда
и наименование этого явления. Коэффициент усиления напряжения равен добротности контура
 . .
Вместе с тем значительное повышение напряжения
на реактивных элементах при резонансе может привести к пробою изоляции
и опасно для обслуживающего персонала.
4. Активная мощность при резонансе максимальна,
так как  , а ток , а ток  максимален. Реактивные мощности на максимален. Реактивные мощности на  и и  равны, равны,
но противоположны по знаку. Это значит, что в те интервалы времени, в течение которых энергия накапливается в магнитном поле индуктивного элемента,
она поступает из электрического поля емкостного элемента. Происходит — обмен энергией между реактивными элементами L и C контура. Источник питания в этом обмене не участвует. В этом обмене энергий и заключается физический смысл резонанса напряжений.
Частотной характеристикой называется зависимость параметров цепи
от частоты. Активное сопротивление R большинства устройств (если речь идет
об ограниченном интервале изменения частоты) от частоты не зависит.
Зависимости индуктивного  и емкостного и емкостного  сопротивлений от частоты определяются формулами: сопротивлений от частоты определяются формулами:  и и  ; они изображены на рис. 3.32. ; они изображены на рис. 3.32.

| 
| | Рис. 3.32. Частичная характеристика
| Рис. 3.33. Резонансные кривые
| Реактивное сопротивление контура  . При . При  
и реактивное сопротивление X носит емкостный характер. При  наступает резонанс напряжений ( наступает резонанс напряжений ( ) и сопротивление контура чисто активное, при ) и сопротивление контура чисто активное, при   и реактивное сопротивление X носит индуктивный характер. и реактивное сопротивление X носит индуктивный характер.
Резонансными кривыми называют зависимости основных величин цепи
(I,  , ,  ) от частоты (рис. 3.33). На том же рисунке показана зависимость ) от частоты (рис. 3.33). На том же рисунке показана зависимость  . Необходимо отметить, что одинаковые максимальные значения напряжений . Необходимо отметить, что одинаковые максимальные значения напряжений 
и  получаются при разных частотах, не совпадающих с резонансной получаются при разных частотах, не совпадающих с резонансной  . .
5. Возникновение максимальной величины тока в цепи и напряжений
на элементах цепи больших, чем напряжения на входе сети (рис. 3.31), делает явление резонанса напряжений опасным режимом в энергообеспечении, который следует избегать из-за возможного выхода реальных объектов из строя.
В схемотехнике явление резонанса напряжений применяют для выделения информации на разных частотах каналов  радио-телевидения, например, радио-телевидения, например,
с использованием узкополосных резонансных усилителей, фильтров и т.д.
Пример 3.12. В цепи с последовательным соединением катушки
с параметрами R, L с конденсатором (рис. 3.34) плавно изменяется емкость C конденсатора. При максимальном токе в цепи сняты показания приборов:  А, А,  В, В, 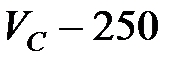 В. Частота тока в цепи 50 Гц. Определить параметры В. Частота тока в цепи 50 Гц. Определить параметры
цепи C, R, L.

Рис. 3.34. Схема к примеру 3.12
и показания вольтметра  , подключенного к выводам катушки. , подключенного к выводам катушки.
Решение. Так как ток максимальный, то в цепи имеет место резонанс напряжений, при котором  В, В,  В. Напряжение на катушке В. Напряжение на катушке
и показание вольтметра 

Емкостное сопротивление

Емкость

При резонансе  , поэтому , поэтому
 и и 

Из формулы  индуктивность индуктивность
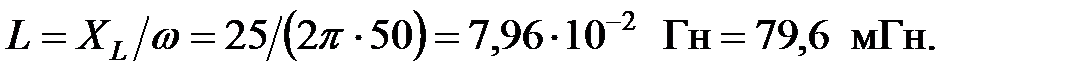
3.3.6. Электрическая цепь переменного синусоидального тока с параллельно соединёнными элементами R, L, C

Рис. 3.35. Схема параллельного соединения
Можно представить реальную электрическую цепь в виде трех идеальных элементов сопротивления, индуктивности и емкости, соединённых параллельно (рис. 3.35).
В этом случае I-й закон Кирхгофа дает следующую формулу в комплексной форме с действующими значениями
 (3.40) (3.40)
и окончательно
 , (3.41) , (3.41)
где: 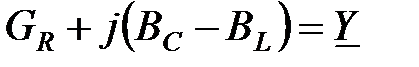 — комплексная полная проводимость, измеряемая — комплексная полная проводимость, измеряемая
в сименсах  ; ;
 — активная проводимость; — активная проводимость;
 — комплексная индуктивная проводимость; — комплексная индуктивная проводимость;
 — комплексная емкостная проводимость. — комплексная емкостная проводимость.
Выражение (3.41) представляет собой закон Ома для параллельной R, L, C цепи.
 , ,
где
 (3.42) (3.42)
 (3.43) (3.43)
Из анализа полученных формул видно, что все величины зависят
от разности  и что существует три соотношения: и что существует три соотношения:
 ; ; 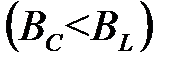 ; ;  . .
Рис. 3.36. Векторные диаграммы R, L, C цепи:
(а)  ; (б) ; (б)  ; (в) ; (в) 
Изучим эти три случая.
1.  . .
В этом случае 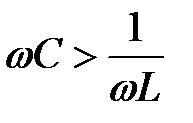 и из выражений (3.40) - (3.43) следует: и из выражений (3.40) - (3.43) следует:
 ( ( ) — сопротивление цепи имеет ) — сопротивление цепи имеет
активно-емкостной характер.
Векторная диаграмма цепи показана на рис. 3.36, а.
Фазовым сдвигом j можно управлять в пределах  изменяя проводимости изменяя проводимости  (3.43). (3.43).
2.  . .
В этом случае  и из выражений (3.40) - (3.43) следует: и из выражений (3.40) - (3.43) следует:
 ( ( ) — сопротивление цепи имеет ) — сопротивление цепи имеет
активно-индуктивный характер.
Векторная диаграмма цепи показана на рис. 3.36, б.
Фазовым сдвигом j можно управлять в пределах  изменяя проводимости изменяя проводимости  (3.43). (3.43).
3.  . .
В этом случае выполняется равенство
 (3.44) (3.44)
и соотношения:
 ( ( ) — сопротивление цепи имеет чисто активный характер. ) — сопротивление цепи имеет чисто активный характер.
Векторная диаграмма цепи показана на рис. 3.36, в.
Этот режим работы цепи получим название резонанс токов. Он реализуется при выполнении условия резонанса (2.44), при котором  ( ( ). Признаком выполнения режима резонанса тока является наличие минимального тока в цепи ). Признаком выполнения режима резонанса тока является наличие минимального тока в цепи  (рис. 3.37). (рис. 3.37).
Из соотношения резонанса токов (3.44) можно вывести формулу
для резонансной частоты 

Из этого выражения следует, что режим резонанса можно получить, изменяя L, C или  (рис. 3.37). (рис. 3.37).

| 
| | Рис. 3.37. График изменения тока цепи
| Рис. 3.38. Векторная диаграмма при резонансе токов
| Рассмотрим характерные особенности контура с малыми потерями
при резонансе токов.
1. Так как  и общее сопротивление контура активное, и общее сопротивление контура активное,
то полная проводимость контура равна активной проводимости и практически минимальна. Эквивалентное сопротивление контура при этом активное
и практически максимальное 
2. Ток в неразветвленной части цепи практически минимальный  , что позволяет обнаруживать резонанс токов в контуре при изменении частоты , что позволяет обнаруживать резонанс токов в контуре при изменении частоты  , параметров , параметров  или или  (рис. 3.37). (рис. 3.37).
3. Реактивные составляющие токов при резонансе равны и 
Если  , то , то  т.е. токи в ветвях значительно больше, чем ток в неразветвленной части цепи (рис. 3.38). Это свойство — усиление тока — является важнейшей особенностью резонанса токов и широко используется на практике. Отсюда и наименование этого явления. т.е. токи в ветвях значительно больше, чем ток в неразветвленной части цепи (рис. 3.38). Это свойство — усиление тока — является важнейшей особенностью резонанса токов и широко используется на практике. Отсюда и наименование этого явления.
4. Коэффициент усиления по току (при резонансе  ) равен добротности контура: ) равен добротности контура: 
5. Как и при резонансе напряжений, между катушкой и конденсатором происходит обмен энергией, но источник питания в этом обмене не участвует: источник только восполняет потери в активных сопротивлениях контура.
В этом обмене и заключается физический смысл резонанса токов.
6. Возникновение в реактивных ветвях токов  и и  значительно больших, чем ток значительно больших, чем ток  потребляемый от сети (рис. 3.38) делает явление резонанса токов опасных режимом в электрообеспечении, который следует избегать из-за возможного выхода реальных объектов из строя. В схемотехнике явление резонанса токов применяют для подавления информации на разных частотах каналов связи. потребляемый от сети (рис. 3.38) делает явление резонанса токов опасных режимом в электрообеспечении, который следует избегать из-за возможного выхода реальных объектов из строя. В схемотехнике явление резонанса токов применяют для подавления информации на разных частотах каналов связи.
Рассмотрим частотную характеристику "идеального" контура ( ). Индуктивная проводимость такого контура ). Индуктивная проводимость такого контура  , а емкостная , а емкостная  . Этим выражениям соответствуют характеристики . Этим выражениям соответствуют характеристики  и и 
и  на рис. 3.39. на рис. 3.39.
Резонансные кривые (рис. 3.40) построены при  в соответствии в соответствии
с определениями токов:  (действующее значение – положительная величина). При (действующее значение – положительная величина). При  контур индуктивный при контур индуктивный при  в контуре имеет место резонанс токов и при в контуре имеет место резонанс токов и при  контур емкостный. контур емкостный.

| 
| | Рис. 3.39. Частотная характеристика контура
| Рис. 3.40. Резонансные кривые
| Пример 3.13. Напряжение на входных выводах контура (рис. 3.41)  В, частота напряжения В, частота напряжения  Гц. Определить емкость Гц. Определить емкость  конденсатора, при которой конденсатора, при которой
в контуре наступает резонанс токов, и токи  в режиме резонанса при в режиме резонанса при
 Ом, Ом,  Ом, Ом,  Ом. Ом.
Решение. Из условия резонанса токов ( ) следует, ) следует,
что  или или  . .
Так как  См, то См, то  , откуда , откуда
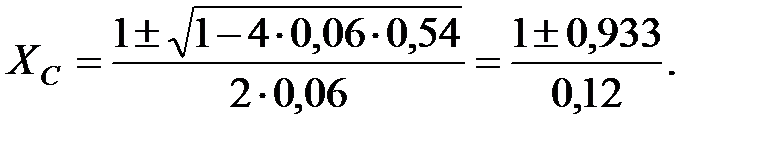
Это уравнение имеет два решения:
 Ом, Ом,  мкФ или мкФ или  Ом, Ом,  мкФ. мкФ.
Из решения следует, что резонанс токов возможен при двух значениях емкости, однако практически целесообразно выбрать меньшую емкость,
т.е.  мкФ. мкФ.
Токи в ветвях (принимая  ): ):
 А; А;
 А; А;
 А. А.

Рис. 3.41. Электрическая цепь к примеру 3.13
Основные положения, изложенные в п. 3.3 материалов:
· Законы Ома и Кирхгофа выполняются в комплексной форме их записи.
· Резистивные, индуктивные и емкостные элементы оказывают гармоническому току сопротивления, причём индуктивные и емкостные элементы оказывают на каждой частоте различные сопротивления, сопротивление же резистивного элемента не зависит от частоты.
· Значения резистивного сопротивления откладывают на вещественной оси комплексной плоскости, значение индуктивного сопротивления — на положительной мнимой полуоси, а значение емкостного сопротивления — на отрицательной мнимой полуоси.
· Комплексное сопротивление объединяет в себе сопротивления резистивных и реактивных элементов.
· Комплексное сопротивление может быть записано в двух основных формах — алгебраической и показательной.
· Аргумент комплексного сопротивления цепи показывает угол сдвига фаз между напряжением и током в этой цепи.
· Модуль комплексного сопротивления цепи показывает соотношение между амплитудами напряжения и тока в этой цепи.
· Сдвиг фаз  между напряжением и током на: резистивном активном сопротивлении равен нулю; индуктивном элементе между напряжением и током на: резистивном активном сопротивлении равен нулю; индуктивном элементе  , емкостном , емкостном  .
· Сдвиг фаз .
· Сдвиг фаз  между напряжением и током на: активно-индуктивном сопротивлении между напряжением и током на: активно-индуктивном сопротивлении  , активно-емкостном , активно-емкостном  .
· В электрических цепях с R, L, C соединениями могут возникнуть режимы "резонанс напряжения", "резонанс токов". Эти режимы опасны в энергообеспечении, но успешно применяются в схемотехнике. .
· В электрических цепях с R, L, C соединениями могут возникнуть режимы "резонанс напряжения", "резонанс токов". Эти режимы опасны в энергообеспечении, но успешно применяются в схемотехнике.
|
|



 -ой закон Кирхгофа для RL -цепи рис.3.21:
-ой закон Кирхгофа для RL -цепи рис.3.21:
 — полное комплексное сопротивление равное
— полное комплексное сопротивление равное ,
, , (3.28)
, (3.28) , (3.29)
, (3.29) .
. приведена на рис. 3.22.
приведена на рис. 3.22.
 — полное комплексное сопротивление равное
— полное комплексное сопротивление равное ,
, , (3.30)
, (3.30) , (3.31)
, (3.31) .
. сдвига фаз между напряжением и током, в пределах указанных выше. Сопротивление
сдвига фаз между напряжением и током, в пределах указанных выше. Сопротивление  в RL цепи имеет характер активно-индуктивный (это значит, что в цепи используется преимущественно тепловая и электромагнитная энергия). Сопротивление
в RL цепи имеет характер активно-индуктивный (это значит, что в цепи используется преимущественно тепловая и электромагнитная энергия). Сопротивление  в RC цепи имеет характер активно-емкостной (это значит, что в цепи используется преимущественно тепловая и электростатическая энергия).
в RC цепи имеет характер активно-емкостной (это значит, что в цепи используется преимущественно тепловая и электростатическая энергия). В,
В,  А. Активное сопротивление катушки
А. Активное сопротивление катушки  Ом. Определить индуктивность катушки, угол сдвига фаз между напряжением и током, построить векторную диаграмму.
Ом. Определить индуктивность катушки, угол сдвига фаз между напряжением и током, построить векторную диаграмму. Ом.
Ом. Ом;
Ом;
 Гц, то
Гц, то  мГн. Напряжения:
мГн. Напряжения:  B;
B;  B.
B. совпадает по фазе с вектором
совпадает по фазе с вектором  , а вектор
, а вектор  опережает его по фазе на угол 90°.
опережает его по фазе на угол 90°.  (рис. 2.25, б).
(рис. 2.25, б). .
. Ом и конденсатор емкостью
Ом и конденсатор емкостью  мкФ (рис. 3.26, а).
мкФ (рис. 3.26, а).  A.
A. Ом.
Ом. В (начальная фаза тока
В (начальная фаза тока  принята равной нулю). Переходя от комплексного выражения к мгновенному значению, получаем:
принята равной нулю). Переходя от комплексного выражения к мгновенному значению, получаем:  B.
B. и
и  Строим векторы напряжений в соответствии с расчетом (рис. 2.36, б).
Строим векторы напряжений в соответствии с расчетом (рис. 2.36, б). В;
В;  B.
B. равен аргументу комплексного сопротивления,
равен аргументу комплексного сопротивления, 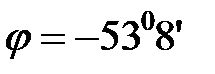 .
. элементами
элементами -го закона Кирхгофа для этой цепи дает следующее уравнение
-го закона Кирхгофа для этой цепи дает следующее уравнение  (3.32)
(3.32)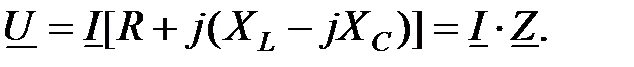 (3.33)
(3.33) цепи, а
цепи, а  — полным комплексным сопротивлением
— полным комплексным сопротивлением  цепи.
цепи. , (3.34)
, (3.34) , (3.35)
, (3.35) (3.36)
(3.36) .
. 


 цепи: (а)
цепи: (а)  ; (б)
; (б)  ;
;

 , и из выражений (3.32) - (3.36) следует:
, и из выражений (3.32) - (3.36) следует: ;
;  ;
;  — сопротивления цепи имеет
— сопротивления цепи имеет  можно управлять, изменяя соотношение
можно управлять, изменяя соотношение  сопротивлений (3.36) в пределах
сопротивлений (3.36) в пределах  .
.
 , и из выражений (3.32) - (3.36) следует:
, и из выражений (3.32) - (3.36) следует: ;
;  ;
;  — сопротивление цепи имеет активно-емкостной характер. Векторная диаграмма цепи показана на рис. 3.28, б. Фазовым углом
— сопротивление цепи имеет активно-емкостной характер. Векторная диаграмма цепи показана на рис. 3.28, б. Фазовым углом  можно управлять в пределах
можно управлять в пределах 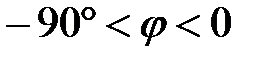 , изменяя соотношения
, изменяя соотношения  сопротивлений (3.36).
сопротивлений (3.36). и
и  изображены на рис. 3.29. Они также отражают
изображены на рис. 3.29. Они также отражают 
 (3.37)
(3.37) ;
;  ;
;  .
.  — сопротивление в цепи имеет чисто активный характер. Векторная диаграмма цепи изображена на рис. 3.28, в,
— сопротивление в цепи имеет чисто активный характер. Векторная диаграмма цепи изображена на рис. 3.28, в,  , (
, ( ,
,  . Признаком выполнения режима резонанса напряжения является наличие максимального значения тока в цепи
. Признаком выполнения режима резонанса напряжения является наличие максимального значения тока в цепи  при достижении
при достижении  значения, как это показано на рис. 3.30.
значения, как это показано на рис. 3.30.
 .
. , индивидуальности
, индивидуальности  или емкости
или емкости  (рис. 3.30). Однако в любом случае явления в цепи при резонансе одинаковые.
(рис. 3.30). Однако в любом случае явления в цепи при резонансе одинаковые. (3.38)
(3.38) (3.39)
(3.39) , то
, то  и суммарное сопротивление участка цепи активное, т.е. полное сопротивление при резонансе равно активному сопротивлению
и суммарное сопротивление участка цепи активное, т.е. полное сопротивление при резонансе равно активному сопротивлению
 максимален
максимален  . Это свойство позволяет обнаружить резонанс напряжений при изменении
. Это свойство позволяет обнаружить резонанс напряжений при изменении 
 или С. Однако резонансный ток при определенных условиях опасен — он может привести к перегреву элементов цепи и выводу их из строя.
или С. Однако резонансный ток при определенных условиях опасен — он может привести к перегреву элементов цепи и выводу их из строя. ;
;  ;
;  .
. , то напряжения на участках контура
, то напряжения на участках контура  ), напряжение на участке с активным элементом
), напряжение на участке с активным элементом  равно напряжению питания на выводах контура и совпадает c ним
равно напряжению питания на выводах контура и совпадает c ним 
 , то
, то  , т.e. напряжение на участках
, т.e. напряжение на участках  .
. , а ток
, а ток  максимален. Реактивные мощности на
максимален. Реактивные мощности на  и
и  равны,
равны,  и емкостного
и емкостного  сопротивлений от частоты определяются формулами:
сопротивлений от частоты определяются формулами:  и
и  ; они изображены на рис. 3.32.
; они изображены на рис. 3.32. . При
. При 

 наступает резонанс напряжений (
наступает резонанс напряжений ( ) и сопротивление контура чисто активное, при
) и сопротивление контура чисто активное, при 
 и реактивное сопротивление X носит индуктивный характер.
и реактивное сопротивление X носит индуктивный характер. ,
,  ) от частоты (рис. 3.33). На том же рисунке показана зависимость
) от частоты (рис. 3.33). На том же рисунке показана зависимость  . Необходимо отметить, что одинаковые максимальные значения напряжений
. Необходимо отметить, что одинаковые максимальные значения напряжений 
 получаются при разных частотах, не совпадающих с резонансной
получаются при разных частотах, не совпадающих с резонансной  .
. радио-телевидения, например,
радио-телевидения, например,  А,
А,  В,
В, 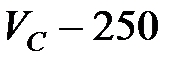 В. Частота тока в цепи 50 Гц. Определить параметры
В. Частота тока в цепи 50 Гц. Определить параметры  , подключенного к выводам катушки.
, подключенного к выводам катушки. В,
В,  В. Напряжение на катушке
В. Напряжение на катушке 


 , поэтому
, поэтому и
и 

 индуктивность
индуктивность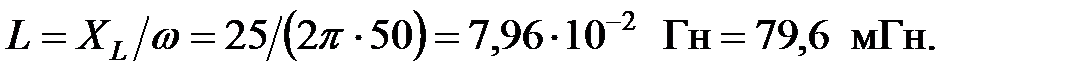
 (3.40)
(3.40) , (3.41)
, (3.41)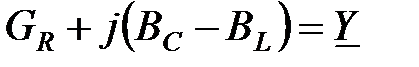 — комплексная полная проводимость, измеряемая
— комплексная полная проводимость, измеряемая  ;
; — активная проводимость;
— активная проводимость; — комплексная индуктивная проводимость;
— комплексная индуктивная проводимость; — комплексная емкостная проводимость.
— комплексная емкостная проводимость. ,
, (3.42)
(3.42) (3.43)
(3.43) и что существует три соотношения:
и что существует три соотношения: ;
; 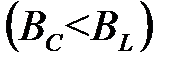 ;
;  .
. ; (б)
; (б)  ; (в)
; (в) 
 .
.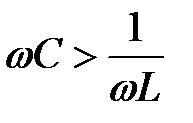 и из выражений (3.40) - (3.43) следует:
и из выражений (3.40) - (3.43) следует: (
( ) — сопротивление цепи имеет
) — сопротивление цепи имеет  изменяя проводимости
изменяя проводимости  (3.43).
(3.43). .
. и из выражений (3.40) - (3.43) следует:
и из выражений (3.40) - (3.43) следует: (
( ) — сопротивление цепи имеет
) — сопротивление цепи имеет  изменяя проводимости
изменяя проводимости  .
. (3.44)
(3.44) (
( ) — сопротивление цепи имеет чисто активный характер.
) — сопротивление цепи имеет чисто активный характер. (
( ). Признаком выполнения режима резонанса тока является наличие минимального тока в цепи
). Признаком выполнения режима резонанса тока является наличие минимального тока в цепи  (рис. 3.37).
(рис. 3.37).

 (рис. 3.37).
(рис. 3.37). и общее сопротивление контура активное,
и общее сопротивление контура активное, 
 , что позволяет обнаруживать резонанс токов в контуре при изменении частоты
, что позволяет обнаруживать резонанс токов в контуре при изменении частоты  , параметров
, параметров  или
или  (рис. 3.37).
(рис. 3.37).
 , то
, то  т.е. токи в ветвях значительно больше, чем ток в неразветвленной части цепи (рис. 3.38). Это свойство — усиление тока — является важнейшей особенностью резонанса токов и широко используется на практике. Отсюда и наименование этого явления.
т.е. токи в ветвях значительно больше, чем ток в неразветвленной части цепи (рис. 3.38). Это свойство — усиление тока — является важнейшей особенностью резонанса токов и широко используется на практике. Отсюда и наименование этого явления. ) равен добротности контура:
) равен добротности контура: 
 и
и  значительно больших, чем ток
значительно больших, чем ток  потребляемый от сети (рис. 3.38) делает явление резонанса токов опасных режимом в электрообеспечении, который следует избегать из-за возможного выхода реальных объектов из строя. В схемотехнике явление резонанса токов применяют для подавления информации на разных частотах каналов связи.
потребляемый от сети (рис. 3.38) делает явление резонанса токов опасных режимом в электрообеспечении, который следует избегать из-за возможного выхода реальных объектов из строя. В схемотехнике явление резонанса токов применяют для подавления информации на разных частотах каналов связи. ). Индуктивная проводимость такого контура
). Индуктивная проводимость такого контура  , а емкостная
, а емкостная  . Этим выражениям соответствуют характеристики
. Этим выражениям соответствуют характеристики  и
и 
 на рис. 3.39.
на рис. 3.39. в соответствии
в соответствии  (действующее значение – положительная величина). При
(действующее значение – положительная величина). При  контур индуктивный при
контур индуктивный при  в контуре имеет место резонанс токов и при
в контуре имеет место резонанс токов и при  контур емкостный.
контур емкостный. В, частота напряжения
В, частота напряжения  Гц. Определить емкость
Гц. Определить емкость  конденсатора, при которой
конденсатора, при которой  в режиме резонанса при
в режиме резонанса при  Ом,
Ом,  Ом,
Ом,  Ом.
Ом. ) следует,
) следует,  или
или  .
. См, то
См, то  , откуда
, откуда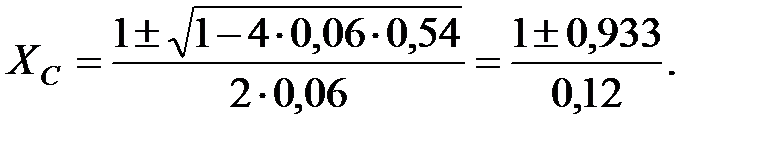
 Ом,
Ом,  мкФ или
мкФ или  Ом,
Ом,  мкФ.
мкФ. мкФ.
мкФ. ):
): А;
А; А;
А; А.
А. между напряжением и током на: резистивном активном сопротивлении равен нулю; индуктивном элементе
между напряжением и током на: резистивном активном сопротивлении равен нулю; индуктивном элементе  , емкостном
, емкостном  .
· Сдвиг фаз
.
· Сдвиг фаз  между напряжением и током на: активно-индуктивном сопротивлении
между напряжением и током на: активно-индуктивном сопротивлении  , активно-емкостном
, активно-емкостном  .
· В электрических цепях с R, L, C соединениями могут возникнуть режимы "резонанс напряжения", "резонанс токов". Эти режимы опасны в энергообеспечении, но успешно применяются в схемотехнике.
.
· В электрических цепях с R, L, C соединениями могут возникнуть режимы "резонанс напряжения", "резонанс токов". Эти режимы опасны в энергообеспечении, но успешно применяются в схемотехнике.



