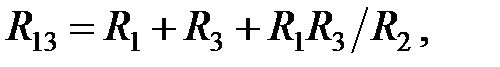Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 2. Электрические цепи постоянного токаСодержание книги
Поиск на нашем сайте Электрическая цепь и элементы цепи Электрическая цепь (рис. 2.1) постоянного тока выглядит следующим образом.
Ток —
Закон Ома. Из (1.5) следует, что падение напряжения на активном резисторе равно произведению величины сопротивления на силу тока протекающего через него:
Откуда сопротивление Величина постоянного напряжения
где:
Из (2.2) следует важный вывод:
Полезная (активная) мощность В ЭЦ рис. 2.1 два элемента потребляют мощность В ЭЦ должен выполняться баланс мощности, физически отражающий закон сохранения энергии. Уравнение баланса:
и для нашего случая В выражении (2.4) составляющие в сумме потребителей мощности имеют только положительные значения и не зависят от знака тока. Составляющие в сумме источников ЭДС Следует учитывать режим работы · направление · направление Пунктиром на рис. 2.1 показан реальный источник ЭДС- Е, отмечающийся Уравнение электрического состояния источника ЭДС будет иметь вид
Аналогичную запись уравнения электрического состояния имеет активная ветвь цепи рис. 2.2, б. Формула 2.5 представляет собой закон Ома для активной ветви ЭЦ. Основные положения, изложенные в п. 2.1 материалов:
2.2. Методы преобразования цепи 2.2.1. Источник, нагруженный на резистор (рис. 2.3) Рис. 2.3. Электрическая цепь под нагрузкой Когда источник питания нагружен активным сопротивлением
откуда
Мощность, выделяемая в сопротивлении
Эта мощность достигает максимума, когда,
и коэффициент полезного действия генератора определится:
Основные характеристики источника, нагруженного на активное сопротивление, Рис. 2.4. Изменение мощности 2.2.2. Закон Кирхгофа Законы Кирхгофа п.1.5 (1.18) и (1.19) запишутся: I Закон Кирхгофа — алгебраическая сумма токов в узле электрической цепи равна нулю
Правило составления уравнений по I закону Кирхгофа — ток, который втекает в узел, имеет положительный знак, который вытекает, отрицательный. Пример для узла Рис. 2.5. Контур электрической цепи II Закон Кирхгофа —в каком-либо контуре ЭЦ алгебраическая сумма электродвижущих сил, действующих в данном контуре, равна алгебраической сумме падений напряжения, в данном контуре:
Правило составления уравнений по II закону Кирхгофа —когда направление обхода контура совпадает с направлением тока в сопротивлении, падение напряжения имеет положительный знак 2.2.3. Последовательное соединение сопротивлений (рис. 2.6) Рис. 2.6. Последовательное соединение В этом случае единственный ток Согласно первому закону Кирхгофа имеем:
откуда
где Для n последовательно включенных сопротивлений будет:
Уравнение баланса мощностей для такой цепи имеет вид:
Последовательное соединение сопротивлений редко используется В схемотехнике последовательное соединение широко используется Правило делителя напряжения: отношение напряжений на элементах последовательной цепи равно отношению сопротивлений этих элементов. Например, для цепи, приведенной на рис. 2.6, по правилу делителя напряжений получим такие выражения для напряжений на ее элементах:
где
2.2.4. Параллельное соединение сопротивлений (рис. 2.7) Единственное напряжение Согласно первому закону Кирхгофа имеем:
откуда
Рис. 2.7. Параллельное соединение Вспомним понятие проводимости (см. п. 1.2), величины обратной сопротивлению
Уравнение баланса мощностей для такой цепи имеет вид:
Частные случаи: 1) Если имеем только два включенных параллельно сопротивления
2) Если имеем несколько одинаковых сопротивлений включенных параллельно, то расчет эквивалентного сопротивления ведем исходя из
откуда для Параллельное соединение сопротивлений широко используется В схемотехнике параллельное соединение широко используется для деления тока. Правило делителя тока: отношение токов в параллельных ветвях равно отношению проводимостей этих ветвей. Для схемы параллельного соединения рис. 2.7 ток
Ток в одной из двух параллельных ветвей равен произведению тока пришедшего к узлу разветвления этих ветвей на сопротивление противоположной ветви, деленному на сумму сопротивлений этих ветвей. 2.2.5. Преобразование схемы «звезда» в «треугольник» и обратно (рис. 2.8) Имеется электрическая цепь в виде треугольного контура, содержащего Можно доказать, что этот контур может быть заменен на эквивалентный Исходя из предложения, что сопротивление а) Из треугольника в звезду:
Рис. 2.8. Электрическая цепь сопротивлений схемы «звезда» (а) и треугольник (б) б) Из звезды в треугольник:
Основные положения, изложенные в п. 2.2 материалов:
|
||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.01 с.) |

 , напряжение
, напряжение  , ЭДС
, ЭДС  обозначаются большими латинскими символами. На схеме пунктиром показан реальный источник ЭДС
обозначаются большими латинскими символами. На схеме пунктиром показан реальный источник ЭДС — потребитель энергии. Величина постоянного тока
— потребитель энергии. Величина постоянного тока 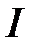 определяется
определяется 
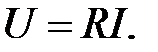 (2.1)
(2.1) , единица измерения которого один Ом.
, единица измерения которого один Ом.  .
. (рис. 2.2, а) определяется:
(рис. 2.2, а) определяется: (2.2)
(2.2) — энергия сторонних сил для переноса единицы заряда
— энергия сторонних сил для переноса единицы заряда  ;
;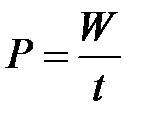 и
и  , соответственно мощность и ток.
, соответственно мощность и ток. —Закон Джоуля-Ленца. (2.3)
—Закон Джоуля-Ленца. (2.3)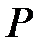 измеряется в ваттах (Вт) и характеризует интенсивность преобразования электрической энергии в тепловую энергию
измеряется в ваттах (Вт) и характеризует интенсивность преобразования электрической энергии в тепловую энергию  , которое в соответствии с п. 1.2 физически отражает способность реальных объектов нагреваться при прохождении постоянного тока, и оценивается в омах (Ом).
, которое в соответствии с п. 1.2 физически отражает способность реальных объектов нагреваться при прохождении постоянного тока, и оценивается в омах (Ом). соответственно
соответственно  и
и  , а один источник энергии с мощностью
, а один источник энергии с мощностью  .
. (2.4)
(2.4) .
. имеют разные знаки в зависимости от режима работы источника энергии.
имеют разные знаки в зависимости от режима работы источника энергии. (рис. 2.1, рис. 2.2) в зависимости:
(рис. 2.1, рис. 2.2) в зависимости: (рис. 2.1) совпадают — источник ЭДС работает в режиме источника энергии и в сумме (2.4) берется знак «+».
(рис. 2.1) совпадают — источник ЭДС работает в режиме источника энергии и в сумме (2.4) берется знак «+». (2.4) берется со знаком «–».
(2.4) берется со знаком «–». и отражающего потери энергии (обычно в виде тепла).
и отражающего потери энергии (обычно в виде тепла). (2.5)
(2.5)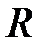 , уравнение электрического состояния ЭЦ запишется:
, уравнение электрического состояния ЭЦ запишется: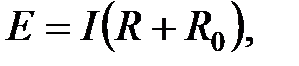

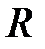 :
:
 (согласованный режим работы ЭЦ см. п.1.3), то есть
(согласованный режим работы ЭЦ см. п.1.3), то есть
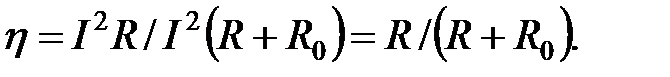
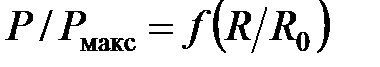 и
и  представлены на рис. 2.4.
представлены на рис. 2.4. и КПД от нагрузки
и КПД от нагрузки 
 (2.6)
(2.6) рис. 2.5:
рис. 2.5:  .
. (2.7)
(2.7) , в тоже время имеет отрицательный знак
, в тоже время имеет отрицательный знак  , если направления не совпадают. Когда направление обхода контура совпадает с направлением ЭДС, имеем положительный знак
, если направления не совпадают. Когда направление обхода контура совпадает с направлением ЭДС, имеем положительный знак  , однако имеем отрицательный знак
, однако имеем отрицательный знак  , если направления не совпадают.
, если направления не совпадают.  рис. 2.5:
рис. 2.5: 

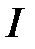 течет через все сопротивления
течет через все сопротивления  .
.
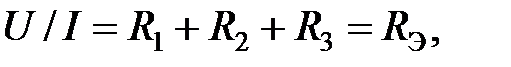
 — эквивалентное сопротивление.
— эквивалентное сопротивление. (2.8)
(2.8)



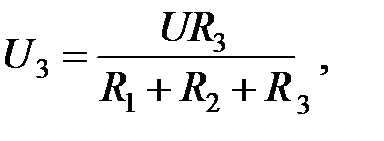
 — общий ток через все сопротивления.
— общий ток через все сопротивления. приложено ко всем сопротивлениям
приложено ко всем сопротивлениям  .
.

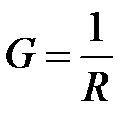 . Тогда для
. Тогда для  включенных параллельно сопротивлений будет:
включенных параллельно сопротивлений будет: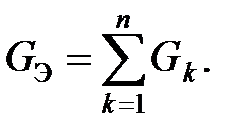 (2.9)
(2.9)
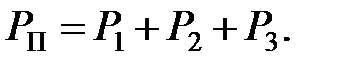
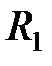 и
и 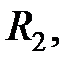 то расчет эквивалентного сопротивления ведем исходя из
то расчет эквивалентного сопротивления ведем исходя из 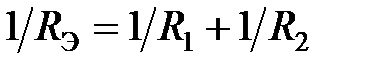 , откуда
, откуда (2.10)
(2.10)
 сопротивлений
сопротивлений  . (2.11)
. (2.11)
 -ой ветви по закону Ома равен
-ой ветви по закону Ома равен  тогда, для двух параллельных сопротивлений (частный
тогда, для двух параллельных сопротивлений (частный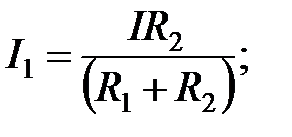

 .
. .
. между точками 1-2, 1-3 и 2-3 этих двух электрических цепей неизменно, можно вывести формулы для взаимного преобразования одной схемы в другую и наоборот:
между точками 1-2, 1-3 и 2-3 этих двух электрических цепей неизменно, можно вывести формулы для взаимного преобразования одной схемы в другую и наоборот: