
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы и методы анализа цепейСодержание книги
Поиск на нашем сайте
1.5.1. Законы электротехники Для расчета цепей недостаточно знать рассмотренные выше в п. 1.2 Важным является закон Ома записанный, например, в форме выражения (1.5), позволяющий находить связь напряжения и токов в простых ветвях. Для описаниявзаимосвязи токов напряжений на разных ветвях используются уравнения соединений (законы Кирхгофа). Первое уравнение соединений (первый закон Кирхгофа)устанавливает взаимосвязь токов в узле (рис. 1.23). Рис. 1.23. Электрическое соединение – узел В узле заряды не могут накапливаться или исчезать. Для узла выполняется закон сохранения заряда — сколько зарядов переносится к узлу втекающими токами, столько же зарядов выходит из узла. После дифференцирования по времени уравнений, описывающих заряды, получаем первый закон Кирхгофа
где втекающие токи берутся со знаком плюс, а вытекающие — со знаком минус
Второе уравнение соединений (второй закон Кирхгофа) устанавливает взаимосвязь напряжений и ЭДС в контурах цепи. Рассмотрим прохождение положительного заряда по контуру (рис. 1.24), направление обхода которого указывается стрелкой. Рис. 1.24. Электрическое соединение – контур По закону сохранения энергии работа сторонних сил в этом контуре должна быть равна работе сил электрического поля. Продифференцировав уравнение, связывающее эти энергии (работы), по заряду, получим соотношение:
Обобщая полученное соотношение для сложного контура, содержащего произвольное число элементов, получим следующую формулировку второго закона Кирхгофа (второго уравнения соединения): в любом контуре цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений. Если стрелки ЭДС или напряжения не совпадают с направлением обхода, то в соответствующую сумму они записываются со знаком минус. Для контура, включающего р ЭДС и
где при согласованных стрелках направления обхода и напряжения на ветви Для расчета линейной электрической цепи любой конечной сложности достаточно использовать два уравнения соединений и рассмотренные в параграфе уравнения элементов (1.5), (1.7), (1.11). Рассмотрим использование этих уравнений для описания процессов цепи, схема которой изображена на рис. 1.24 записывая для контура этой цепи второй закон Кирхгофа:
Коэффициенты этого уравнения являются константами и определяются параметрами элементов схемы. В правой части таких уравнений записываются члены, содержащие заданные токи или напряжения. Полученное выражение называется неоднородным линейным дифференциальным уравнением цепи. Легко убедиться в том, что процессы в любой другой линейной электрической цепи также описываются неоднородными линейными дифференциальными уравнениями. Общие методы решения этих уравнений излагаются в курсе математического анализа. Отдельные, наиболее часто используемые в электротехнике Если в цепи имеется хотя бы один нелинейный элемент, то цепь становится нелинейной. Нелинейная цепь описывается нелинейным дифференциальным уравнением. Для параметрической цепи, содержащей, по крайней мере, один параметрический элемент, получим параметрическое дифференциальное уравнение. Для линейной электрической цепи справедлив принцип суперпозиции (наложения). Поясним этот принцип на примере цепи, схема которой изображена на рис. 1.25. Рис. 1.25. Схема с двумя источниками ЭДС В цепи, включающей последовательно соединенные резистор, катушку
Пусть на цепь воздействует только один сигнал
Пусть теперь напряжение
Суммируя левые и правые части этих уравнений и используя известные свойства интеграла и производной — интеграл или производная от суммы функций равны сумме интегралов или производных от каждой из функций, окончательно получим:
Из анализа формулы следует, что воздействие суммы сигналов Принцип суперпозиции часто используется для расчета цепей, содержащих несколько источников тока и (или) напряжения, например, в радиотехнике процесс модуляции. Неиспользуемые источники при расчете реакции на одно воздействие исключаются следующим образом: источники напряжения — методом замыкания выводов (короткого замыкания), а источники тока методом разрыва ветви (холостого хода). Этот принцип суперпозиции широко используется на практике инженерами. Например, при расчете усилительного каскада (рис. 1.26) отдельно анализируют работу каскада на транзисторе в режиме постоянного тока (статический режим), который определяется напряжениями смещения Рис. 1.26. Транзисторный усилительный каскад Наряду с принципом суперпозиции при анализе и расчете ЭЦ полезны теорема (взаимности) и теорема (принцип) компенсации. Не приводя доказательств, запишем только формулировки этих теорем. Теорема обратимости (взаимности): если ЭДС, включенная на входе линейной цепи, вызывает некоторый ток на выходе, то та же ЭДС, перенесенная К обратимым цепям относятся пассивные электрические цепи, не содержащие источников. Простой пример цепи, где действует теорема обратимости, — двухпроводная (телефонная) линия связи с двумя абонентами. Очевидно, что такая линия передачи информации обратима и абонентов в этой линии можно поменять местами.
Теорема компенсаций токи в электрической цепи не изменятся, если любой участок цепи заменить "компенсационной" ЭДС, равной по величине напряжению на данном участке и направленной навстречу этому напряжению. Доказательство этой теоремы следует из рассмотрения уравнений цепи, записанных 1.5.2. Методы анализа цепей Законы электротехники Ома, I и II Кирхгофа реализуются в методах анализа ЭЦ. Методы, применяемые для расчета реакции цепи на то или иное воздействие, зависят от вида воздействия, источника энергии. Если воздействие не зависит от времени, находится в режиме постоянного тока. При этом все индуктивности в цепи представляются, как известно, короткими замыканиями (т.е. отрезками проводов), а все емкости — разрывами цепи. Оставшиеся в эквивалентной схеме резистивные сопротивления образуют чисто резистивную цепь. Нахождение напряжений и токов в такой цепи от любых источников не представляет сложностей. Методы расчета электрических цепей Неизменное во времени воздействие (т.е. постоянный ток или постоянное напряжение) характеризуется только одним параметром — величиной Следует заметить, что при гармоническом воздействии на линейную электрическую цепь расчет напряжений на элементах и токов в ветвях усложняется. Дело в том, что реактивные элементы (индуктивность и емкость) оказывают влияние не только на амплитуду гармонической реакции, но и изменяют
При заданной частоте гармонических колебаний в цепи воздействия представляются комплексными числами (или векторами на комплексной плоскости при графическом изображении). Реакции цепи будут представляться также комплексными числами, но с другими амплитудами и начальными фазами. Задача анализа цепи — найти эти амплитуды и начальные фазы. Представление воздействий и реакций в виде комплексных чисел позволяет использовать для расчета (анализа) цепи тот же арсенал методов, который используется для цепей с постоянными воздействиями, с той лишь разницей, Тот факт, что периодическое воздействие сложной формы можно представить в виде суммы гармонических колебаний разных частот, лежит в основе расчета цепей с источниками периодических негармонических сигналов (например, последовательностей прямоугольных, пилообразных, треугольных и тому подобных импульсов). Из математики известно, что представление периодической функции суммой гармонических колебаний называется разложением этой функции Набор гармонических колебаний кратных частот, описывающий периодический сигнал, называется спектром этого сигнала. Анализ изменения спектра сигнала на выходе цепи по сравнению со спектром входного сигнала позволяет сказать, как изменился сам сигнал при прохождении его по цепи. Адекватным математическим аппаратов для представления непериодических воздействий является интегралом Фурье. Два интегральных преобразования Фурье (прямое и обратное) позволяют Расчет реакции линейной цепи с источниками непериодических сигналов, называемый спектральным анализом, подробно описан в работах [1, 2, 8, 9]. Обобщением интегральных преобразований Фурье являются интегральные преобразования Лапласа, которые позволяют определять операторные изображения воздействий и, наоборот, форму воздействий по их изображениям. Поэтому вместо спектрального анализа цепи может быть проведен операторный анализ, суть которого состоит в отыскании сначала операторного изображения реакции, а затем с помощью обратного преобразования Лапласа — реакции цепи
Существует прямой путь вычисления реакции цепи на воздействие, не прибегая к определению спектров или изображений сигналов. В математике известны так называемые интегралы свертки, которые дают возможность найти реакцию цепи на непериодическое воздействие путем прямого вычисления интеграла свертки. Анализ линейных цепей с помощью интегралов свертки, или временной метод анализа, изучается в [1, 8, 9]. На практике часто встречаются случаи, когда в цепи происходят коммутации. Коммутацией принято называть любое изменение параметров цепи, ее конфигурации, подключение или отключение источников, приводящие к возникновению переходных процессов. Анализ переходных процессов приведен в [1, 3, 4, 9]. Если цепь содержит нелинейные резисторы (диоды, транзисторы), то чаще всего используют графоаналитические методы расчета. Как правило, в цепях Подобно тому, как аналоговые воздействия были представлены преобразованиями Фурье и Лапласа, дискретные воздействия представляются Основные положения, изложенные в п. 1.5 материалов:
1.6. Вопросы и задания для самопроверки 1. Сформулируйте законы Кирхгофа и Ома. 2. Дайте определение тока, напряжения, ЭДС, электрического потенциала, разности потенциалов. 3. Поясните физические процессы, происходящие в простейшей замкнутой электрической цепи. 4. Поясните, что такое ветвь, узел, контур электрической цепи. 5. Перечислите особенности согласованного режима, режимов холостого хода и короткого замыкания. 6. Когда при расчетах токи и напряжения в цепи получаются отрицательными? Что означает отрицательное значение тока или напряжения? 7. Что показывает стрелка положительного направления для переменного тока, значения которого могут быть как положительными, так и отрицательными? 8. Рассматривая простейшие конструкции катушки и конденсатора и силовые линии полей в них, определить элемент, который при прочих равных условиях легче обнаружить. 9. Рассчитайте ток через конденсатор, если напряжение на нем линейно возрастает с течением времени. 10. Докажите, что напряжения на конденсаторах и токи через катушки индуктивности не могут изменяться скачками. 11. Найдите напряжение на катушке, если ток через нее возрастает с течением времени по линейному закону (по экспоненциальному закону, квадратично). 12. Когда в первое уравнение соединений для узла (первый закон Кирхгофа) токи записываются со знаком минус? Поясните это правило, исходя из закона сохранения заряда. 13. В каком случае во второе уравнение соединений (второй закон Кирхгофа) напряжения и ЭДС записываются со знаком минус? Поясните это правило, исходя из закона сохранения энергии (работы). 14. В какой цепи мгновенная мощность электрического тока может быть отрицательной? Что означает отрицательная величина мгновенной мощности? 15. Почему для съема информации с участка цепи удобнее использовать вольтметры, амперметры? 16. Как известно, наиболее часто встречающаяся неисправность
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.142.42 (0.01 с.) |

 , используется следующая математическая запись первого закона Кирхгофа:
, используется следующая математическая запись первого закона Кирхгофа: (1.18)
(1.18)
 — второй закон Кирхгофа. Если стрелка напряжения или ЭДС противоположна направлению обхода, то эти ЭДС или напряжение должны записываться в формулу со знаком минус.
— второй закон Кирхгофа. Если стрелка напряжения или ЭДС противоположна направлению обхода, то эти ЭДС или напряжение должны записываться в формулу со знаком минус. ветвей, используется следующая математическая запись второго закона Кирхгофа:
ветвей, используется следующая математическая запись второго закона Кирхгофа: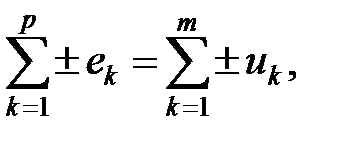 (1.19)
(1.19)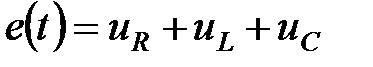 и учитывая уравнения элементов, получим интегро-дифференциальное уравнение цепи
и учитывая уравнения элементов, получим интегро-дифференциальное уравнение цепи  . Дифференцируя это выражение, получим дифференциальное уравнение электрической цепи для одной из неизвестных величин — тока цепи:
. Дифференцируя это выражение, получим дифференциальное уравнение электрической цепи для одной из неизвестных величин — тока цепи:
 и
и 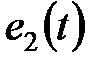 . В контуре цепи как реакция
. В контуре цепи как реакция 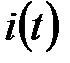 .
.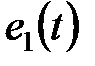 (сигнал
(сигнал 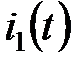 возникающего под действием ЭДС
возникающего под действием ЭДС 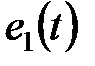 имеет вид:
имеет вид:
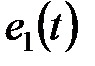 равно нулю и на цепь воздействует сигнал
равно нулю и на цепь воздействует сигнал  Дифференциальное уравнение для тока
Дифференциальное уравнение для тока  возникающего под действием ЭДС
возникающего под действием ЭДС 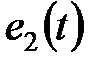 , имеет аналогичный вид:
, имеет аналогичный вид:
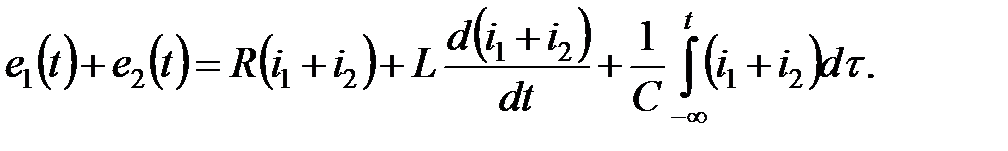
 вызывает появление реакции — результирующего тока
вызывает появление реакции — результирующего тока  , равно сумме токов
, равно сумме токов  возникающих от каждого из сигналов в отдельности.
возникающих от каждого из сигналов в отдельности.  и питания
и питания  , и отдельно рассчитывают напряжения и токи, обусловленные воздействием на усилитель входного сигнала
, и отдельно рассчитывают напряжения и токи, обусловленные воздействием на усилитель входного сигнала  (динамический режим). Полный анализ состоит
(динамический режим). Полный анализ состоит 


