
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графические методы анализа нелинейных электрических цепейСодержание книги
Поиск на нашем сайте
Последовательное или параллельное соединение нескольких НЭ удобно анализировать с помощью, обобщенной ВАХ НЭЦ, полученной графическим объединением ВАХ всех НЭ, при этом учет влияния источников сводится На рис. 2.29 приведен пример последовательного соединения линейного Рис. 2.29. Последовательное соединение НЭ и ВАХ Иногда целесообразно применять метод опрокинутой ВАХ (рис. 2.30). Рис. 2.30. Последовательное соединение НЭ и ВАХ На рис. 2.31 приведен пример параллельного соединения линейного и двух нелинейных элементов. Рис. 2.31. Схема параллельного соединения и ВАХ При смешанном (параллельном и последовательном) соединений НЭ задача построения обобщенной ВАХ решается последовательно: сначала строится ВАХ Рис. 2.32. Смешанное соединение НЭ и ВАХ Наличие ВАХ всех элементов ЭЦ позволяет определять все токи Пример 2.10. Линейный элемент с сопротивлением Рис. 2.33. Схема к примеру 2.10
Определить ток в цепи рис. 2.33 и напряжение на нелинейном элементе. Решение. Воспользуемся методом пересечения характеристик — графическим решением системы двух уравнений, выражающих связь между напряжением Зависимость Рис. 2.34. ВАХ элементов Точка
Масштабы тока и напряжения равны:
Пример 2.11. Стабилизатор напряжения (рис. 2.35) выполнен на стабилитроне ВАХ которого изображена на рис. 2.36 (кривая 1). Стабилитрон включен параллельно сопротивлению нагрузки, напряжение на котором требуется стабилизировать; Рис. 2.35. Схема к примеру 2.11 Определить границы изменения напряжения питания Решение. Воспользоваться методом построения ВАХ цепей Проводим ВАХ сопротивления нагрузки Рис. 2.36. ВАХ к примеру 2.11 Пример 2.12. На рис. 2.37 представлена схема цепи транзисторного усилителя, содержащая источник коллекторного питания Определить в каких пределах в схеме рис. 2.37. будет изменяться ток коллекторной цепи Рис. 2.37. Схема усилителя постоянного тока Решение. Схема рис. 2.37 может быть представлена в виде эквивалентной схемы рис. 2.39. Нелинейный элемент в схеме рис. 2.39 — управляемый нелинейный элемент, семейство ВАХ которого приведено на рис. 2.38. Применяем для схемы рис. 2.39 метод пересечения характеристик (см. линию нагрузки, построенную по двум точкам:
при
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.55.42 (0.008 с.) |

 .
.
 (рис. 2.33).
(рис. 2.33). (I) выражается, с одной стороны, вольтамперной характеристикой нелинейного элемента, заданной табл. 2.1 и рис. 2.34, а с другой — уравнением
(I) выражается, с одной стороны, вольтамперной характеристикой нелинейного элемента, заданной табл. 2.1 и рис. 2.34, а с другой — уравнением  , составленным по второму закону Кирхгофа. Последнее уравнение является уравнением внешней характеристики активного двухполюсника, к которому подключен нелинейный элемент. Эта прямая может быть построена по двум точкам с координатами
, составленным по второму закону Кирхгофа. Последнее уравнение является уравнением внешней характеристики активного двухполюсника, к которому подключен нелинейный элемент. Эта прямая может быть построена по двум точкам с координатами  ,
,  и
и  ,
,  (рис. 2.34).
(рис. 2.34). пересечения характеристик определяет корни этой системы уравнений:
пересечения характеристик определяет корни этой системы уравнений:  и
и  . Прямую
. Прямую  называют опрокинутой характеристикой нелинейного элемента, т.к. её можно построить по-другому: провести прямую из точки, а под углом
называют опрокинутой характеристикой нелинейного элемента, т.к. её можно построить по-другому: провести прямую из точки, а под углом  к вертикали:
к вертикали:

 — сопротивление резистора для гашения части напряжения.
— сопротивление резистора для гашения части напряжения. , при которых
, при которых 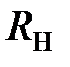 (с учетом масштабов) —
(с учетом масштабов) — , суммируя токи при фиксированных значениях напряжения — кривая 3; резистора
, суммируя токи при фиксированных значениях напряжения — кривая 3; резистора  практически изменяет напряжение на
практически изменяет напряжение на  при токе в цепи
при токе в цепи 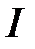 .
. , резистор коллекторной цепи
, резистор коллекторной цепи  и биполярный транзистор Т — управляемый нелинейный элемент. Семейство ВАХ управляемого элемента
и биполярный транзистор Т — управляемый нелинейный элемент. Семейство ВАХ управляемого элемента  приведено на рис. 2.38.
приведено на рис. 2.38. , если пределы изменения тока базы
, если пределы изменения тока базы 
 ,
,  и
и 
 ) и определяем диапазон изменения тока базы
) и определяем диапазон изменения тока базы  : при
: при  ,
,  (точка N на рис. 2.38),
(точка N на рис. 2.38),
 (точка
(точка  на рис. 2.38). Следовательно,
на рис. 2.38). Следовательно,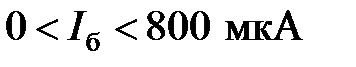 для тока коллектор справедливо неравенство
для тока коллектор справедливо неравенство  Рабочую точку РТ транзистора выбираем посредине диапазона изменения
Рабочую точку РТ транзистора выбираем посредине диапазона изменения  и
и 



