Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод непосредственного применения законов КирхгофаСодержание книги
Поиск на нашем сайте
Идея метода. Законы Кирхгофа (2.6) и (2.7) наиболее общие, универсальные законы, описывающие режим работы электрической цепи, и метода расчета, основанные на этих законах, применимы к расчету режима любой электрической цепи. Однако в практике расчетов их чаще всего применяют для определения токов в ветвях сложных цепей с несколькими источниками электрической энергии. Порядок расчета. При расчете рекомендуется определенная последовательность решения, которая далее иллюстрируется на примере расчета токов в схеме рис. 2.15 при заданных сопротивлениях и ЭДС. 1. Определяется число ветвей, т.е. число неизвестных токов, и узлов, которые обозначаются буквами или цифрами (1, 2, 3, 0 на рис. 2.15); выбираются произвольно и указывается положительные направления токов. 2. Определяется, сколько уравнений нужно составить по первому закону Кирхгофа и сколько по второму. Общее число уравнений должно быть равно числу неизвестных токов, т. е. числу ветвей Для схемы рис. 2.15 число ветвей 3. Составляются уравнения. При составлении
Для схемы рис. 2.15 составим три уравнения по первому закону Кирхгофа
По второму закону Кирхгофа составим три уравнения (направление обхода контуров примем по направлению движения часовой стрелки):
Рис. 2.15. Разветвленная схема ЭЦ Рис. 2.16. Схема к примеру 2.3 Решив уравнения совместно, найдем искомые токи. Если численное значение какого-либо тока в ветви получается отрицательным, то это означает, что его действительное направление противоположно выбранному положительному (в этих случаях изменять принятое направление тока не рекомендуется). Пример 2.3. Дана схема рис. 2.16. ЭДС Решение. 1. Между точками, 2. Схема имеет два узла и четыре ветви, поэтому по первому закону Кирхгофа надо составить 3. Составим одно уравнение по первому закону для узла а:
В полученную систему уравнений подставим численные значения ЭДС
Решим систему уравнений (2.12) − (2.15) методом подстановки. Из (2.13) Подставим значения
откуда Ток 2.3.5. Метод контурных токов Это широко распространенный метод расчета сложных электрических цепей
При этих предположениях оказывается, что для расчета схемы достаточно ограничиться составление уравнений для контурных токов только по второму закону Кирхгофа, так как для контурных токов только по второму закону Кирхгофа, так как для контурных токов первый закон выполняется в силу принятых Порядок расчета токов в ветвях цепи следующий: 1. Произвольно выбирают направления токов ветвях. 2. Выбирают независимые контуры, а затем задают направления условных токов, который называют контурными токами. 3. Для каждого из выбранных контуров составляют систему линейных независимых уравнений по закону напряжений Кирхгофа порядка 4. Определяют токи в ветвях исходной цепи как алгебраическую сумму контурных токов, протекающих по этой ветви. Поясним метод на примере схемы рис. 2.15. Выше для этой схемы было получено, что В канонической форме записи составляем систему уравнений для контурных токов порядка
Определяем коэффициенты системы:
При составлении уравнений (2.16) пользуются правилами знаков: собственное сопротивление всегда берется со знаком "плюс"; взаимное сопротивление берется со знаком "плюс", если контурные токи протекают через него в одном направлении, и со знаком "минус" — если в разных направлениях; напряжение источника в правой части (2.16) берется со знаком "плюс", если его направление противоположно направлению контурного тока, и со знаком Подставляем найденные коэффициент в систему (2.16) и получаем
Так как направление обхода контура совпадает с направлением тока в этом контуре, то падения напряжения от этого тока записывается со знаком плюс. Решив уравнения (2.17), используя найденные меры аппарата алгебраической матрицы, совместно определим контурные токи
Токи ветвей: Пример 2.4. Решить пример 2.3 методом контурных токов. Решение. Выберем независимые контуры (рис. 2.16) — внутренние контуры (ячейки) схемы, положительные направления контурных токов
Подставим заданные численные значения, получим:
Решив систему уравнений, найдем контурные токи: Составим баланс мощности:
и после подставленных величин получаем:
Баланс мощности сошелся и можем сделать заключение — пример 2.4 решен верно. 2.3.6. Метод узловых напряжений Метод узловых напряжений (потенциалов) основан на законе токов Кирхгофа и законе Ома и позволяет уменьшить количество уравнений в системе до 1. Произвольно выбирают направление токов в ветвях; 2. Заземляют один из узлов (любой, называемый базисным); его потенциал поэтому становится равным нулю. 3. Составляют систему линейных независимых уравнений для узлов цепи 4. Используя законы Ома для пассивного и активного участков цепи, находят токи в ветвях исходной схемы. Рассмотрим применение метода узловых напряжений для расчета токов ветвях цепи, изображенной на рис. 2.15 (на этой схеме, также изображенной на рис. 2.15, рассмотрены примеры расчета методами непосредственного применения законов Кирхгофа и контурных токов). Направление токов в ветвях выбираем произвольно. Заземляем любой узел, например, «0» (базисный узел). Это означает, что его потенциал равен нулю: Для узлов 1, 2 и 3 составляем систему независимых уравнений по I закону Кирхгофа порядка В канонической форме записи система уравнений имеет вид
В уравнениях (2.18) использованы обозначения: Определяем коэффициенты системы:
При составлении уравнений пользуются правилами знаков: собственные проводимости всегда берутся со знаком «плюс», взаимные проводимости всегда берутся со знаком «минус», узловые токи источников берутся со знаком «плюс», если ЭДС направлены к узлу, и со знаком «минус» — если от узла.
Подставляем найденные коэффициенты в систему (2.18) и получаем уравнения по первому закону Кирхгофа:
Решив уравнения (2.19) совместно используя, например, аппарат алгебраической матрицы, определяем электрические потенциалы Зная потенциалы узлов, находим токи в ветвях цепи рис. 2.15, Используя законы Ома (2.1) и (2.5) находим токи в ветвях
Если использование закона Ома для пассивных цепей не вызывает вопросов, то закон Ома для активных ветвей требует комментариев из возможной разнонаправленности На рис. 2.17 приведена схема активной ветви. Используя II закон Кирхгофа имеем:
откуда
Выражение (2.20) и есть закон Ома для активной цепи, при использовании которого следует учесть, что в виде (2.20) закон записан для направлений векторов рис. 2.17. При изменении направления какого-либо из векторов, необходимо менять знак перед соответствующей величиной в (2.20). Пример 2.5. Выбрать метод и рассчитать схему рис. 2.18. Дано: Решение. Выбираем метод, учитывая сложность расчета. Число ветвей Используем для расчета метод узловых напряжений, как наиболее простой. Выберем произвольное напряжение токов в ветвях. Заземлим потенциал узла 3
Вычислим коэффициенты системы:
Подставив выше найденные коэффициенты в систему и вычислим потенциалы узлов:
Найдем токи в ветвях, используя законы Ома:
Меняем направления токов Составим баланс мощности:
Баланс сошелся, и задача решена правильно.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 381; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.235.107 (0.01 с.) |

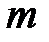 . По первому закону составляется
. По первому закону составляется  уравнений, где
уравнений, где  -число узлов схемы (уравнение для одного из узлов является следствие остальных, т.е. не является независимым; оно может быть получено суммированием всех остальных
-число узлов схемы (уравнение для одного из узлов является следствие остальных, т.е. не является независимым; оно может быть получено суммированием всех остальных  независимых уравнений.
независимых уравнений. , число узлов
, число узлов  . По первому закону Кирхгофа необходимо составить
. По первому закону Кирхгофа необходимо составить  уравнения, а по второму
уравнения, а по второму  уравнения.
уравнения. уравнений по первому закону Кирхгофа токам, направленным от узла, приписывается знак плюс,
уравнений по первому закону Кирхгофа токам, направленным от узла, приписывается знак плюс,  записывается со знаком плюс, если направление обхода ветви совпадает с положительным направлением тока, и со знаком минус в противном случае.
записывается со знаком плюс, если направление обхода ветви совпадает с положительным направлением тока, и со знаком минус в противном случае. — узел 1;
— узел 1;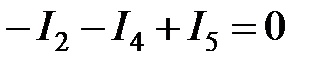 — узел 2;
— узел 2;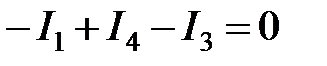 — узел 3.
— узел 3. — контур I;
— контур I; — контур II;
— контур II; — контур III.
— контур III.

 внутренние сопротивления источников
внутренние сопротивления источников 

 Сопротивления
Сопротивления 

 Определить токи в ветвях.
Определить токи в ветвях. и
и  нет включенного сопротивления
нет включенного сопротивления 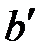 и
и  . Следовательно, схема имеет два узла, между которым четыре ветви и число неизвестных токов равно четырем. Выбранные положительные направления токов показаны на схеме.
. Следовательно, схема имеет два узла, между которым четыре ветви и число неизвестных токов равно четырем. Выбранные положительные направления токов показаны на схеме. уравнение, а по второму —
уравнение, а по второму —  уравнения.
уравнения.
 — контур I;
— контур I; — контур II;
— контур II; — контур III
— контур III (2.12)
(2.12) (2.13)
(2.13) (2.14)
(2.14) (2.15)
(2.15) из (2.14),
из (2.14), 

 в (2.12), получим:
в (2.12), получим:
 затем найдем:
затем найдем: 


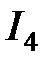 получился отрицательным, значит на рис. 2.16 неправильно выбрали его направление. Меняем направление
получился отрицательным, значит на рис. 2.16 неправильно выбрали его направление. Меняем направление 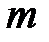 уравнений при непосредственном применении законов Кирхгофа достаточно составить
уравнений при непосредственном применении законов Кирхгофа достаточно составить  уравнений,
уравнений,  . Решение этой системы уравнений позволит найти все контурные токи.
. Решение этой системы уравнений позволит найти все контурные токи. . Выделим для этой схемы три независимых контура
. Выделим для этой схемы три независимых контура . Направление контурных токов можно выбрать произвольно, но для единообразия последующих формул и расчетов следует (если возможно) задавать контурным токам направления, совпадающие
. Направление контурных токов можно выбрать произвольно, но для единообразия последующих формул и расчетов следует (если возможно) задавать контурным токам направления, совпадающие  :
: (2.16)
(2.16) — получил название контурное (собственное) сопротивление,
— получил название контурное (собственное) сопротивление,  контур;
контур; — получил название межконтурное (взаимное) сопротивление,
— получил название межконтурное (взаимное) сопротивление,  контурами;
контурами; — получил название контурное ЭДС, равное алгебраической сумме ЭДС включенных в
— получил название контурное ЭДС, равное алгебраической сумме ЭДС включенных в  (2.17)
(2.17)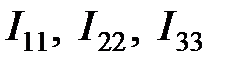 . Токи ветвей равны алгебраическим суммам контурных токов. При этом знаки у контурных токов определяем по следующему правилу: если направление контурного тока совпадает
. Токи ветвей равны алгебраическим суммам контурных токов. При этом знаки у контурных токов определяем по следующему правилу: если направление контурного тока совпадает  ;
;  ;
;  ;
;  ;
;  ;
;  .
. ;
;  ;
;  ;
;  ;
;  ;
; 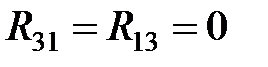 ;
;  ;
;  ;
;  .
.


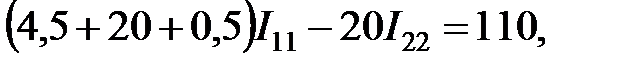

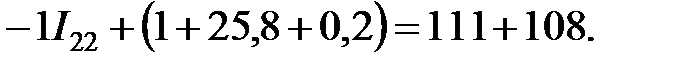


 Токи в ветвях:
Токи в ветвях: 



 Меняем направление
Меняем направление 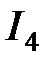 на рис. 2.16
на рис. 2.16
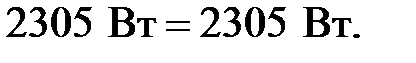
 . Порядокрасчета токов в ветвях цепи следующий:
. Порядокрасчета токов в ветвях цепи следующий: . Решение данной системы позволяет найти напряжения (разность потенциалов) между узлами.
. Решение данной системы позволяет найти напряжения (разность потенциалов) между узлами. .
. .
. (2.18)
(2.18)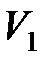 ,
,  ,
,  — потенциалы узлов 1, 2 и 3 цепи;
— потенциалы узлов 1, 2 и 3 цепи; — получил название собственная проводимость узла,
— получил название собственная проводимость узла,  — получил название взаимная проводимость узлов,
— получил название взаимная проводимость узлов, 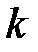 и
и  узлами;
узлами; — получил название узловой ток, равный сумме произведений ЭДС
— получил название узловой ток, равный сумме произведений ЭДС  .
. (2.19)
(2.19) ,
,  и
и  .
.




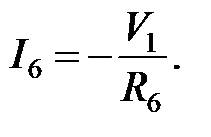


 (2.20)
(2.20)









 .
. число узлов
число узлов  . Метод непосредственного применения законов Кирхгофа требует расчета
. Метод непосредственного применения законов Кирхгофа требует расчета  уравнений; метод контурных токов –
уравнений; метод контурных токов –  уравнения; метод узловых напряжений –
уравнения; метод узловых напряжений –  уравнения.
уравнения.











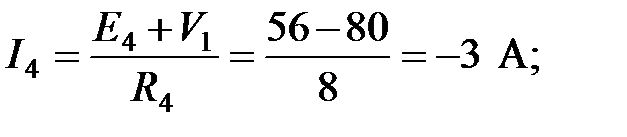


 ,
, 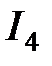 ,
,  на рис. 2.18 на противоположное (стрелки пунктиром) и делаем вывод по режиму работы ЭДС:
на рис. 2.18 на противоположное (стрелки пунктиром) и делаем вывод по режиму работы ЭДС:  — потребитель энергии;
— потребитель энергии;  — источник энергии;
— источник энергии;  — источник энергии;
— источник энергии;  — потребитель энергии.
— потребитель энергии.