
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет спектрального состава тока в резистивном нелинейном элементе при гармоническом воздействииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте За счёт нелинейности ВАХ происходит искажение формы тока, протекающего через нелинейный элемент при воздействии на него гармонического напряжения; Рис. 4.17. Усилитель на биполярном транзисторе На рис. 4.18 изображены проходная ВАХ транзисторного каскада, зависимость во времени напряжения на входе каскада Рис. 4.18. Линейный режим работы транзисторного усилителя Иная картина будет наблюдаться, если напряжение смещения Рис. 4.19. Нелинейный режим работы транзисторного усилителя. Искажение формы тока из-за нелинейности ВАХ Рис. 4.20. Работа транзисторного усиителя в режиме нижней отсечки тока Рис. 4.21. ВАХ диода Рис. 4.22. Одностороннее и двухстороннее ограничения напряжения с помощью диодных ограничителей Из теории спектрального анализа сигналов известно, что любой периодический сигнал может быть представлен рядом Фурье (используя косинусоидальную форму воздействия сигнала (см. п. 3.1.)). Это значит,
Искажения формы сигнала из-за нелинейности ВАХ называют нелинейными искажениями. Если перед нами стоит задача усилить сигнал без искажений (например, при воспроизведении речи, музыки, изображения и т.п.), то следует выбирать такой режим работы (напряжение смещения и амплитуды сигналов), чтобы не выходить за пределы линейного участка ВАХ. Наоборот, стремление преобразовать сигнал с помощью нелинейного элемента, например, не дать мгновенному значению сигнала превысить некоторый заранее установленный порог, приводит к необходимости работать в режиме больших нелинейных искажений. На рис. 4.21 изображена вольт-амперная характеристика диода. Приближенно можно считать, что при воздействии на диод напряжения в "прямом направлении" (правая полуплоскость рисунка) через него будет протекать ток, т.е. На практике широко применяются схемы диодных ограничителей напряжения (рис. 4.22). Здесь диод выполняет роль вентиля: в открытом состоянии его сопротивление мало (десятки Ом), в закрытом состоянии — очень велико (сотни МОм). Эти свойства диода позволяют аппроксимировать его ВАХ кусочно-линейной функцией (рис. 4.23). Напряжением смещения Рис. 4.23. Аппроксимация ВАХ диода кусочно-линейной функцией Состав спектра тока в нелинейном элементе при аппроксимации ВАХ степенным полиномом определяется степенью полинома и его коэффициентами. Ограничимся рассмотрением полиномов со степенью не выше третьей. График полинома первой степени
представляет собой прямую Для определения амплитуд гармоник тока подставим в (4.14) выражение
Сравнивая это выражение с рядом Фурье
видим, что График полинома второй степени
содержит в дополнение к графику полинома первой степени квадратичную параболу Подставляя в (4.15) напряжение
Это выражение показывает, что если вольт-амперная характеристика нелинейного элемента имеет нелинейность, описываемую квадратичной параболой, то в спектре тока, протекающего через такой нелинейный элемент, появляется Для описания нелинейности ВАХ более высокого порядка используется полином третьей степени:
в котором добавляется так называемая кубическая парабола Подстановка напряжения
где постоянная составляющая Из приведенных примеров видно, что наличие в ВАХ нелинейностей высокого порядка приводит к появлению высших гармоник в спектре тока. Спектр тока при кусочно-линейной аппроксимации ВАХ зависит от угла отсечки. При больших амплитудах гармонического напряжения, подводимого
График тока при этом имеет вид косинусоидальных импульсов с отсечкой. Половина той части периода в радианах (или градусах), в течение которой протекает ток, называется углом отсечки. Он обозначен на рис. 4.24 буквой Из графика на рис. 4.24 можно вычислить угол отсечки
Рис. 4.24. Постороение графика тока при кусочно-линейной аппроксимации ВАХ Рис. 4.25. Функции Берга Последнее равенство показывает, что угол отсечки можно изменять, меняя напряжение смещения Периодическую последовательность импульсов тока на рис. 4.24 можно разложить в ряд Фурье:
Опуская процедуру нахождения коэффициентов ряда Фурье Постоянная составляющая и амплитуды гармоник тока вычисляются
где функции Чтобы получить максимальные амплитуды гармоник, следует выбирать Таким образом, амплитуды спектральных составляющих тока в нелинейном элементе при кусочно-линейной аппроксимации его ВАХ зависят от угла отсечки. Количество гармоник при этом бесконечно большое. Чем меньше угол отсечки При воздействии на нелинейный элемент суммы гармонических колебаний возникают спектральные составляющие с комбинированными частотами.
называется бигармоническим воздействием. Спектр бигармонического воздействия изображен на рис. 4.26, а. Пусть на вход НЭ, ВАХ которого аппроксимирована полиномом второй степени
поданы напряжение смещения
Используя тригонометрические формулы а) б) Рис. 4.26. Спектры бигармонического напряжения (а) и тока (б) в нелинейном элементе
и
получаем
Спектральный состав тока в цепи с НЭ показан на рис. 4.26, б. Принципиально новым по сравнению с воздействием на НЭ одного гармонического колебания здесь является появление спектральных составляющих с комбинационными частотами Таблица 4.1. Комбинационные частоты при аппроксимации ВАХ нелинейного элемента полиномом третьей степени
Основные положения, изложенные в п. 4.2 материалов:
4.3. Вопросы и задания для самопроверки 1. Какие резистивные элементы называются нелинейными? 2. Какие методы используют для расчета нелинейных цепей в режиме постоянного тока? 3. Каким образом формируются уравнения состояния нелинейных резистивных цепей? 4. Каков порядок расчета резистивных цепей с нелинейными четырехполюсниками? 5. Какие существуют методы аппроксимации ВАХ нелинейных элементов? 6. Каков физический смысл действующих значений несинусоидальных токов и напряжений? 7. Определите действующее значение несинусоидального тока:
(Ответ: 8. Дайте определения активной, реактивной и полной мощностей несинусоидального тока. Найдите активную и полную мощности цепи, если:
(Ответ: 9. Объясните методику расчета тока в линейной цепи (см. рис. 4.3)
если параметры цепи 10. Покажите, как влияют реактивные элементы с параметрами 11. Объясните принцип работы низкочастотного фильтра на примере электрической цепи, приведенной на рис. 4.5. 12. Поясните принцип работы резонансных фильтров и их назначение (рис. 4.8 и рис. 4.9).
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

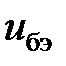 , состоящее из напряжения смещения
, состоящее из напряжения смещения 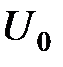 и гармонического напряжения с амплитудой
и гармонического напряжения с амплитудой 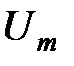 . Под действием входного напряжения в цепи коллектора транзистора протекает коллекторный ток
. Под действием входного напряжения в цепи коллектора транзистора протекает коллекторный ток 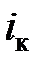 . Зависимость коллекторного тока от напряжения на участке «база — эмиттер» является проходной вольт-амперной характеристикой.
. Зависимость коллекторного тока от напряжения на участке «база — эмиттер» является проходной вольт-амперной характеристикой.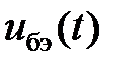 и зависимость
и зависимость 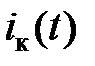 . Напряжение смещения
. Напряжение смещения  и амплитуда гармонического напряжения
и амплитуда гармонического напряжения  выбраны на рисунке таким образом, что рабочая точка не выходит за пределы линейного участка ВАХ. В результате коллекторный ток будет содержать постоянную составляющую
выбраны на рисунке таким образом, что рабочая точка не выходит за пределы линейного участка ВАХ. В результате коллекторный ток будет содержать постоянную составляющую  и гармоническую составляющую с амплитудой
и гармоническую составляющую с амплитудой  .
. уменьшить
уменьшить 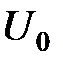 приведет к еще большему искажению формы тока (рис. 4.20).
приведет к еще большему искажению формы тока (рис. 4.20).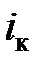 складывается из постоянной составляющей, основной составляющей с частотой входного сигнала и высших гармоник:
складывается из постоянной составляющей, основной составляющей с частотой входного сигнала и высших гармоник:
 . (4.13)
. (4.13)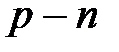 переход диода будет открыт, а при воздействии напряжения в "обратном направлении" (левая полуплоскость рисунка) ток практически протекать не будет, т.е.
переход диода будет открыт, а при воздействии напряжения в "обратном направлении" (левая полуплоскость рисунка) ток практически протекать не будет, т.е. 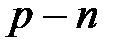 переход диода будет закрыт.
переход диода будет закрыт. регулируют порог ограничения.
регулируют порог ограничения. (4.14)
(4.14)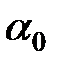 , параллельную оси абсцисс, и наклонную прямую
, параллельную оси абсцисс, и наклонную прямую  с коэффициентом наклона
с коэффициентом наклона 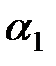 смещенную по оси абсцисс на величину
смещенную по оси абсцисс на величину  . Регулируя величины
. Регулируя величины  ,
, 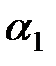 и
и  можно перемещать аппроксимирующую прямую вниз, вправо и влево и менять ее наклон.
можно перемещать аппроксимирующую прямую вниз, вправо и влево и менять ее наклон. :
: .
. ,
, ;
;  ;
;  . Таким образом, при аппроксимации ВАХ полиномом первой степени ток содержит кроме постоянной составляющей
. Таким образом, при аппроксимации ВАХ полиномом первой степени ток содержит кроме постоянной составляющей 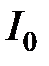 только основную (первую) гармонику, совпадающую по частоте с приложенным гармоническим напряжением. Высшие гармоники в спектре тока отсутствуют, нелинейных искажений нет.
только основную (первую) гармонику, совпадающую по частоте с приложенным гармоническим напряжением. Высшие гармоники в спектре тока отсутствуют, нелинейных искажений нет. (4.15)
(4.15) смещенную по оси абсцисс на величину
смещенную по оси абсцисс на величину  Квадратичный член служит
Квадратичный член служит  , получаем:
, получаем:
 .
.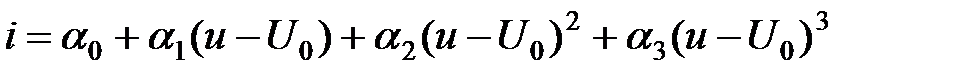 ,
,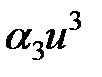 , смещенная по оси абсцисс на величину
, смещенная по оси абсцисс на величину 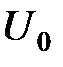 .
. в этот полином дает
в этот полином дает
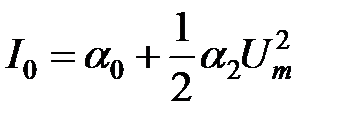 и амплитуды гармоник
и амплитуды гармоник 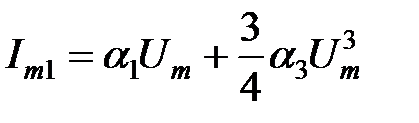 ,
,  и
и  .
.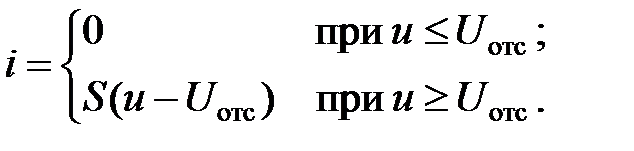 (4.16)
(4.16)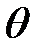 .
. .
.  напряжение
напряжение 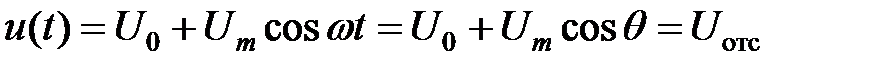 . Откуда
. Откуда и
и  . (4.17)
. (4.17)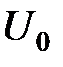 , амплитуду гармонического сигнала
, амплитуду гармонического сигнала  или выбирая параметр
или выбирая параметр 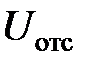 аппроксимирующей функции (4.16).
аппроксимирующей функции (4.16).
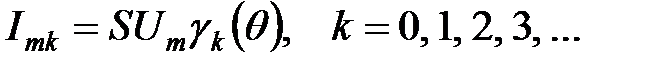 , (4.18)
, (4.18) называются функциями Берга (в честь крупного российского радиотехника академика А.И. Берга). Они зависят от угла отсечки, и их значения для разных углов отсечки приводятся в справочниках. Графики нескольких функций Берга представлены на рис. 4.25.
называются функциями Берга (в честь крупного российского радиотехника академика А.И. Берга). Они зависят от угла отсечки, и их значения для разных углов отсечки приводятся в справочниках. Графики нескольких функций Берга представлены на рис. 4.25. , так как при таких углах отсечки функции Берга
, так как при таких углах отсечки функции Берга 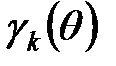 принимают максимальные значения.
принимают максимальные значения. и
и  и амплитудами
и амплитудами  и
и  :
: ,
,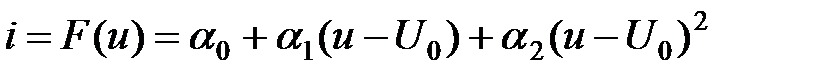 ,
, и бигармонический сигнал
и бигармонический сигнал 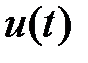 .
. 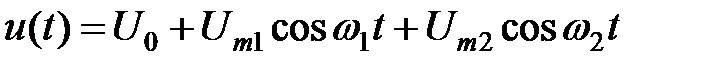 в выражение для ВАХ позволяет определить ток в цепи НЭ в виде
в выражение для ВАХ позволяет определить ток в цепи НЭ в виде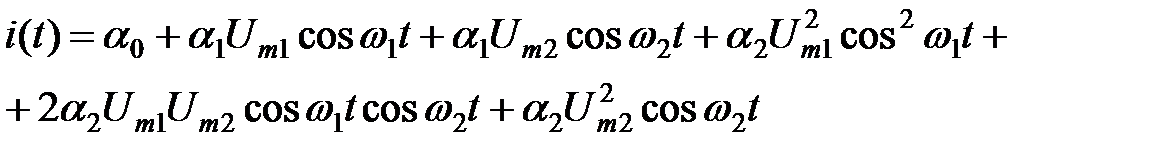
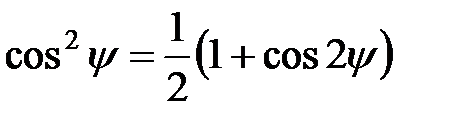
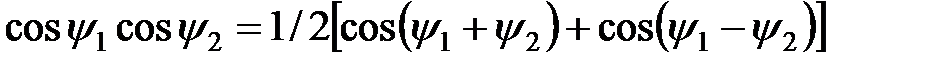 ,
, (4.19)
(4.19)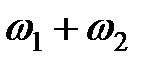 и
и 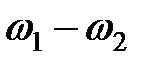 . Если ВАХ нелинейного элемента аппроксимирована в общем случае полиномом степени
. Если ВАХ нелинейного элемента аппроксимирована в общем случае полиномом степени  , то в спектральном составе тока будут присутствовать составляющие с комбинационными частотами
, то в спектральном составе тока будут присутствовать составляющие с комбинационными частотами  , причем
, причем  , где
, где  и
и  — целые положительные числа (0, 1, 2,...). Так, например, при аппроксимации ВАХ нелинейного элемента полиномом третьей степени в составе спектра тока присутствуют комбинационные частоты, приведенные в табл. 4.1.
— целые положительные числа (0, 1, 2,...). Так, например, при аппроксимации ВАХ нелинейного элемента полиномом третьей степени в составе спектра тока присутствуют комбинационные частоты, приведенные в табл. 4.1.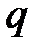



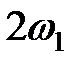




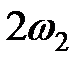
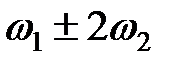
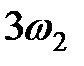

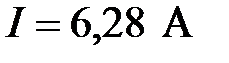 ).
).

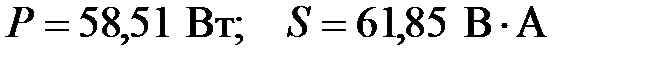 ).
).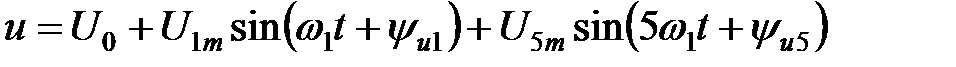 ,
,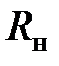 ,
,  и
и  заданы.
заданы. и
и 



