
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт цепей с несколькими источникамиСодержание книги
Поиск на нашем сайте
Все методы, используемые для расчёта электрических цепей в режиме постоянного тока, применимы и к расчёту цепей при гармоническом воздействии. Методы наложения, узловых напряжений, контурных токов, эквивалентного генератора используются для определения реакций в цепи с несколькими источниками гармонических колебаний (см. п. 2.3). Расчёт выполняется для символической формы записи токов, напряжений Пример 3.15. Найдем токи и напряжения в цепи, изображенной на рис. 3.43, если заданы значения Во-первых, определим комплексное сопротивление
Рис. 3.43. Схема для расчёта токов и напряжений в символической форме Рис. 3.44. Эквивалентная схема
Рис. 3.45. Схемы для определения тока Сопротивление Получаем эквивалентную схему, изображенную на рис. 3.44. Эквивалентное комплексное сопротивление цепи определяется как
Ток (рис. 3.45) определяется по закону Ома:
Токи
Следует отметить, что согласно закону токов Кирхгофа
Определим напряжения на элементах цепи (рис. 3.43):
Согласно закону напряжений Кирхгофа векторная диаграмма напряжений замкнута (рис. 3.47)
Пример 3.16. Проиллюстрируем различные методы расчета на примере достаточно простой цепи, изображенной на рис. 3.48. ЭДС источника Рис. 3.48. Схема к примеру 3.16 Решение методом непосредственного применения законов Кирхгофа
и два по второму закону Кирхгофа
Подставив заданные величины, получим три уравнения с тремя неизвестными:
Решив уравнения совместно, определим искомые токи:
Решение методом контурных токов (см. п. 2.3.5). Для двух внутренних контуров (ячеек) составим уравнения по второму закону Кирхгофа для контурных токов:
Подставив в уравнения численные значения, получим два уравнения с двумя неизвестными контурными токами:
Решив уравнения совместно, определим значения контурных токов и токов
Решение методов двух узлов (см. п. 2.3.7). Напряжение между узлами a и b определим по формуле (2.21), но при комплексных значениях всех величин:
Токи в ветвях найдем по закону Ома:
Решение методом наложения (см. п. 2.3.3). Для заданной цепи (рис. 3.48) построим две вспомогательные схемы с одним источником ЭДС в каждой Рассчитаем токи во вспомогательных схемах при выбранных положительных направлениях. а) Для схемы рис. 3.49, а:
Рис. 3.49. Вспомогательные схемы к рис. 3.48
б) Для схемы рис. 3.49, б:
Токи в заданной цепи равны алгебраическим суммам токов вспомогательных схем:
Основные положения, изложенные в п. 3.5 материалов:
3.6. Комплексные передаточные функции В отличие от коэффициента передач резистивной цепи (см. п. 2.4) коэффициент передачи в цепях синусоидального тока имеет комплексную форму. Рассмотрим электрическую цепь, изображенную на рис. 3.50. Нас может интересовать любая реакция цепи (напряжение или ток в любом элементе или ветви цепи) на любое из приложенных воздействий. Предположим, что воздействие создается источником Рис. 3.50. Электрическая цепь с тремя источниками энергии Рис. 3.51. Представление цепи на рис. 3.50 в виде четырехполюсника Рис. 3.52. Символическое изображение напряжений и токов в цепи рис. 3.51 Символическое изображение напряжений и токов на входе и выходе четырехполюсника показано на рис. 3.52. Важнейшей характеристикой линейной электрической цепи является комплексная передаточная функция
В зависимости от того, что считается реакцией и воздействием, различают следующие виды передаточных функций.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 155; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.13.83 (0.006 с.) |

 ,
,  ,
,  ,
,  ,
, 
 параллельного соединения резистора
параллельного соединения резистора 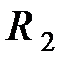 и емкостного сопротивления
и емкостного сопротивления  :
:

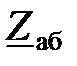 можно представить в виде
можно представить в виде 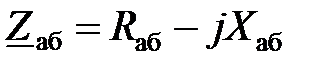 .
. Ом.
Ом. А.
А.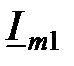 и
и  определяем по формулам разброса:
определяем по формулам разброса: А;
А;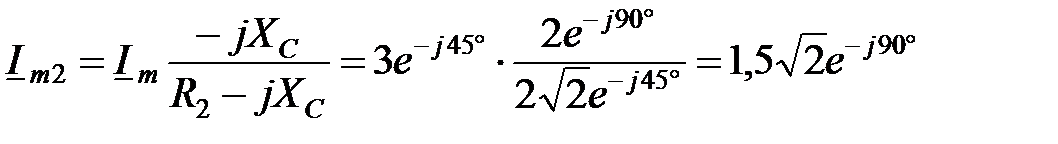 А.
А. . Векторная диаграмма токов приведена на рис. 3.46.
. Векторная диаграмма токов приведена на рис. 3.46. В;
В; В;
В; В.
В. .
. В,
В,  В, комплексные сопротивления
В, комплексные сопротивления  Ом,
Ом,  Ом,
Ом, Ом. Требуется определить токи в ветвях различными методами.
Ом. Требуется определить токи в ветвях различными методами.
 ;
; 



 А;
А;  А;
А;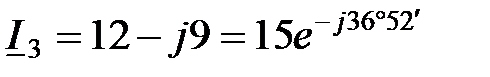 А.
А.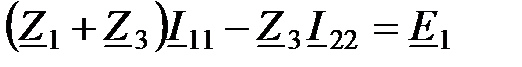 ;
;  .
. ;
; .
. А;
А;  А;
А; А.
А. В.
В. А;
А;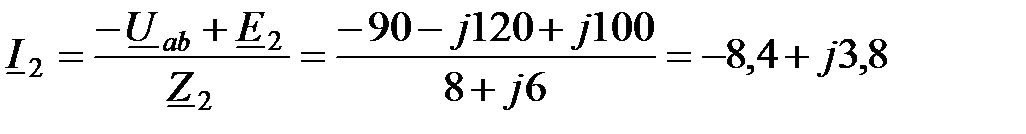 А;
А; А.
А. А.
А. В;
В; А;
А; А.
А. А;
А;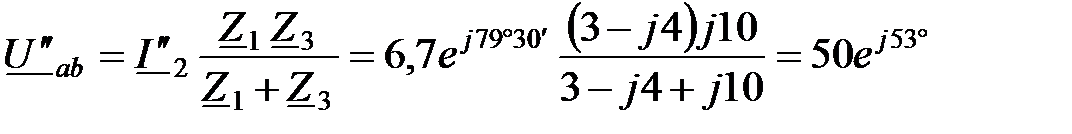 В;
В; А;
А; А.
А.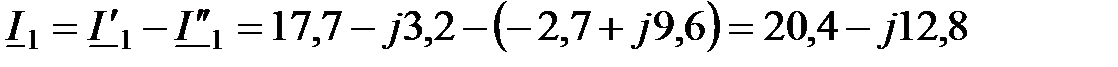 А;
А; А;
А; А.
А. , а реакцией является ток
, а реакцией является ток  . В этом случае цепь удобно представить четырехполюсником, на входе которого включен источник с заданным воздействием, а на выходе — интересующий нас элемент, например, как это сделано на рис. 3.51.
. В этом случае цепь удобно представить четырехполюсником, на входе которого включен источник с заданным воздействием, а на выходе — интересующий нас элемент, например, как это сделано на рис. 3.51. . Она определяется отношением комплексной амплитуды реакции к комплексной амплитуде воздействия.
. Она определяется отношением комплексной амплитуды реакции к комплексной амплитуде воздействия.


