
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные величины, характеризующие синусоидальные функции времениСодержание книги
Поиск на нашем сайте
В линейных цепях синусоидального тока и напряжение, и ЭДС, и ток являются синусоидальными функциями времени:
здесь Как следует из (3.1), каждая синусоидальная функция времени однозначно определяется тремя параметрами: амплитудой Рис. 3.3. Графики синусидального напряжения угловой частотой начальной фазой Кроме того, для характеристики синусоидальных функций времени используют следующие величины: 1) период 2) частота 3) сдвиг фаз между напряжением и током 4) действующее значение
В соответствии с определением действующее, т.е. среднеквадратичное, значение синусоидального тока:
Аналогично определяются действующие значения напряжения и ЭДС: 5) среднее значение Мгновенное значение тока
Аналогично определяются средние значения напряжения и ЭДС:
Рис. 3.4. Графики мгновенного значения токов На рис. 3.4 показаны:
Угол
Когда Когда Когда Действующее (эффективное) значение тока I может быть определено Представление синусоидальных величин в виде, показанном на рис. 3.3 Пример 3.1. Построим графики напряжения
Для построения графиков гармонических колебаний
Напряжение Период
Найдем моменты времени
получаем
Графики
Основные положения, изложенные в п. 3.1 материалов:
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.219.166 (0.01 с.) |

 ;
;  ;
;  (3.1)
(3.1) — соответственно мгновенные значения напряжения, ЭДС, тока,
— соответственно мгновенные значения напряжения, ЭДС, тока, 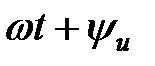 ,
,  ,
,  — аргументы синусоидальных функций, называемые фазой или фазовым углом. Фаза отсчитывается от точки перехода синусоидальной функции через нуль к положительному значению. Синусоидальные напряжение
— аргументы синусоидальных функций, называемые фазой или фазовым углом. Фаза отсчитывается от точки перехода синусоидальной функции через нуль к положительному значению. Синусоидальные напряжение  и ток
и ток  показаны
показаны  (максимальное значение синусоидальной функции);
(максимальное значение синусоидальной функции); (скорость изменения аргумента синусоидальной функции), где
(скорость изменения аргумента синусоидальной функции), где  — в рад/с.;
— в рад/с.; (значение аргумента синусоидальной функции в момент начала отсчета времени, т.е. при
(значение аргумента синусоидальной функции в момент начала отсчета времени, т.е. при  ) в радианах или градусах.
) в радианах или градусах. — наименьший интервал времени, по истечении которого мгновенные значения периодической величины повторяются.
— наименьший интервал времени, по истечении которого мгновенные значения периодической величины повторяются. , т.е. число периодов в секунду. Единица частоты — герц (Гц) (
, т.е. число периодов в секунду. Единица частоты — герц (Гц) ( ). На практике часто используются частоты, измеренные
). На практике часто используются частоты, измеренные  Гц,
Гц, Гц.
Гц. — алгебраическая величина, определяемая как разность начальных фаз, напряжения и тока:
— алгебраическая величина, определяемая как разность начальных фаз, напряжения и тока:  .
. ;
; —среднеквадратичное значение переменной величины за период. Наименование "действующее" объясняется тем, что тепловой и силовой эффекты синусоидального тока за период равны тепловому эффекту постоянного тока, значение которого равно действующему значению синусоидального тока за тот же интервал времени. Так, при синусоидальном токе
—среднеквадратичное значение переменной величины за период. Наименование "действующее" объясняется тем, что тепловой и силовой эффекты синусоидального тока за период равны тепловому эффекту постоянного тока, значение которого равно действующему значению синусоидального тока за тот же интервал времени. Так, при синусоидальном токе  в сопротивлении
в сопротивлении  та же электрическая энергия преобразуется
та же электрическая энергия преобразуется 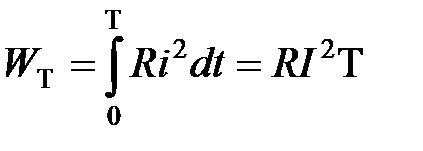 .
. (3.2)
(3.2) ;
;  . Важно знать, что в паспорте электротехнических устройств синусоидального тока указаны действующие значения напряжений и токов и что большинство приборов, применяемых
. Важно знать, что в паспорте электротехнических устройств синусоидального тока указаны действующие значения напряжений и токов и что большинство приборов, применяемых  . Среднее значение синусоидальной функции за период равно нулю (одинаковые площади положительной
. Среднее значение синусоидальной функции за период равно нулю (одинаковые площади положительной  показано на рис. 3.4.
показано на рис. 3.4. . По определению среднего значения имеем:
. По определению среднего значения имеем: (3.3)
(3.3) ;
; 
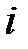 — мгновенное значение тока (А),
— мгновенное значение тока (А), — максимальное значение тока (амплитуда) (А),
— максимальное значение тока (амплитуда) (А), — действующее значение тока (А),
— действующее значение тока (А), — период (сек),
— период (сек), — угловая частота (рад/сек),
— угловая частота (рад/сек),  , где
, где  (Гц),
(Гц), — начальная фаза (град) или (рад).
— начальная фаза (град) или (рад). определяет разность фаз, например:
определяет разность фаз, например: ;
; 
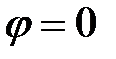 , эти две величины находятся в фазе.
, эти две величины находятся в фазе. , эти две величины находятся в квадратуре.
, эти две величины находятся в квадратуре. , эти две величины находятся в противофазе.
, эти две величины находятся в противофазе. и тока
и тока  , заданные выражениями
, заданные выражениями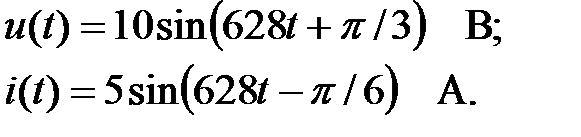
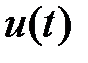 и
и  определим, используя (3.1), их амплитуды
определим, используя (3.1), их амплитуды 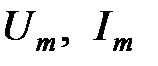 и начальные фазы
и начальные фазы  :
:

 — опережающее колебание, а ток
— опережающее колебание, а ток  — запаздывающее колебание.
— запаздывающее колебание. колебаний
колебаний 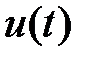 и
и  найдем
найдем
 и
и  , при которых
, при которых  и
и  принимают значения, равные нулю. Из равенств:
принимают значения, равные нулю. Из равенств:
 мс,
мс, 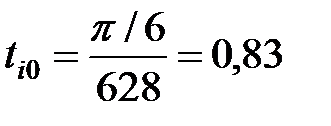 мс.
мс. и
и  приведены на рис. 3.5.
приведены на рис. 3.5. и
и 



