
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 5. Переходные процессы в линейных электрических цепяхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Переходные процессы возникают в электрических цепях при различных воздействиях, приводящих к изменению их режима работы, т.е. при действии различного рода коммутационной аппаратуры, например ключей, переключателей для включения или отключения источника или приемника энергии, при обрывах Существенную роль играют переходные процессы в схемотехнике. Отметим, что физической причиной возникновения переходных процессов Переходный процесс в цепи описывается дифференциальным уравнением — неоднородным или однородным, если ее схема замещения содержит или В дальнейшем ограничимся расчетом переходных процессов в линейных цепях, содержащих элементы с постоянными параметрами. Для решения линейных дифференциальных уравнений с постоянными параметрами разработаны различные аналитические методы: классический, операторный, метод интеграла Фурье и другие, которые применяются и для расчета переходных процессов. Ограничимся применением классического метода, как обладающего физической наглядностью и удобством для расчета простых цепей, а название метода "классический" отражает использование в нем решений дифференциальных уравнений с постоянными параметрами методами классической математики. Расчет переходного процесса в цепи классическим методом содержит следующие этапы. 1. Прежде всего, необходимо составить систему уравнений на основе законов Кирхгофа, Ома, электромагнитной индукции и т.д., описывающих состояние цепи после коммутации, и исключением переменных получить одно дифференциальное уравнение, в общем случае неоднородное относительно искомого тока 2. Далее следует составить общее решение полученного неоднородного дифференциального уравнения цепи в виде суммы частного решения неоднородного дифференциального уравнения и общего решения соответствующего однородного дифференциального уравнения. Применительно к электрическим цепям в качестве частного решения неоднородного дифференциального уравнения выбирают (принужденный) режим, установившийся цепи (если он существует), т. е. постоянные токи и напряжения, если в цепи действуют источники постоянных ЭДС и токов, или синусоидальные напряжения и токи при действии источников синусоидальных ЭДС и токов. Токи Общее решение однородного дифференциального уравнения описывает процесс в цепи без источников ЭДС и тока, который поэтому Свободный процесс вызывается несоответствием между энергией, сосредоточенной в электрическом и магнитном полях емкостных и индуктивных элементов в момент времени, непосредственно предшествовавший коммутации, 3. Наконец, в общем решении Постоянные интегрирования определяют из начальных условий, т.е. условий в цепи в начальный момент времени после коммутации. Будем считать коммутационные ключи идеальными, т. е. что коммутация в заданный момент времени Законы коммутации утверждают, что ток в индуктивном элементе Анализ энергетических процессов в индуктивном элементе приводит
где Анализ энергетического процессов в емкостном элементе приведет к выводу: изменение напряжения на емкостном элементе скачком невозможно (см. п. 1.2). Этот вывод является вторым законом коммутации, который записывается в виде
где Токи в индуктивных элементах Если токи в индуктивных элементах и напряжения на емкостных элементах цепи в момент времени В соответствие с методикой, расчёта переходных процессов классическим методом схематично рассмотрим примеры расчёта. 5.1. Переходные процессы в цепи с последовательным соединением элементов R, L, C (рис. 5.1) Рис. 5.1. Схема включения R, L, C цепи При замыкании ключа К, для цепи с последовательным соединением элементов R, L и C, т.е. последовательного контура (рис. 5.1), согласно второму закону Кирхгофа для мгновенных значений имеем
или, так как
т.е. получается линейное дифференциальное неоднородное уравнение второго порядка для напряжения на емкости Такого же вида уравнение можно получить и для тока
Решение любого из уравнений (5.3) или (5.4) даст результат расчёта переходного режима цепи по току и напряжения. Выберем дифференциальное уравнение цепи
Его решение ищем в виде
Частное решение: Если Рис. 5.2. Схема установившегося режима R, L, C цепи установившиеся значения будут равны
Общее решение для свободной составляющей В этом случае получим схему (рис. 5.3) и дифференциальное уравнение
Рис. 5.3. Схема для свободного режима R, L, C цепи Решение такого уравнения для напряжения получается в виде
и тогда ток будет
Здесь:
Полное решение для напряжения на емкости представляет сумму
и для тока
Начальные условия решения уравнений находятся согласно законам коммутации (5.1) и (5.2): 1) Ток в цепи с индуктивностью не может измениться скачком
2) Напряжение на емкости не может измениться скачком
Решение для
откуда получаем постоянные интегрирования
Однако характер переходного процесса зависит от корней характеристического уравнения
Рассмотрим три случая по порядку: 1) если 2) если 3) если Рис. 5.4. Графики 5.2. Заряд конденсатора через резистор (рис. 5.5) Рис. 5.5. Схема заряда емкости Дифференциальное уравнение цепи
и его решение находим в виде
Частное решение Если
Общее решение В этом случае дифференциальное уравнение будет
и его решение всегда получается в виде
где:
Величина Полное решение уравнения для напряжения находим как сумма
Начальное условие согласно закону коммутации определяется формулой:
и тогда Следовательно
а ток
где Таким образом, ток в этой цепи изменяется скачком и затем спадает до нуля, Рис. 5.6. Напряжение и ток при заряде емкости 5.3. Разряд конденсатора через резистор (рис. 5.7) Дифференциальное уравнение будет таким же, как при заряде конденсатора, однако
Решение уравнения находим в виде
Рис. 5.7. Схема разряда емкости Частно Частное решение Если
Общее решение В этом случае решение получается в виде
Полное решение уравнения для напряжения находим как сумма
Начальное условие согласно закону коммутации определяется формулой:
и тогда Следовательно
а ток
где То есть как и в предыдущем случае ток в этой цепи изменяется скачком Рис. 5.8. Напряжение и ток при разряде емкости 5.4. Подключение индуктивности к источнику постоянной ЭДС через резистор (рис. 5.9) Рис. 5.9. Схема включения индуктивности Дифференциальное уравнение электрического состояния такой цепи будет
и его решение для тока получим в виде
Частное решение Если
Общее решение В этом случае дифференциальное уравнение будет
и его решение всегда получается в виде
где:
Величина Полное решение уравнения для тока находим как сумма
Начальное условие согласно закону коммутации определяется формулой:
и тогда Следовательно
Напряжение на резисторе определим по закону Ома
а на индуктивности —исходя из формулы
На рисунке 5.10 представлены кривые тока и напряжений на резисторе Рис. 5.10. Напряжение и ток в цепи при включении индуктивности Постоянная времени В заключение отметим, что расчёт переходных процессов в более сложных вариантах электрических цепей и разными методами приведен в работах [1, 3, 4, 10]. Основные положения, изложенные в гл. 5 материалов:
5.5. Вопросы и задания для самопроверки 1. Объясните, что понимается под переходным процессом в электрической цепи и каковы причины его возникновения. 2. Приведите примеры использования переходных процессов 3. Составьте для цепи, представленной на рис. 5.9 (в режиме отключения 4. Объясните, какой метод расчета называется классическим и что понимается под установившейся и свободной составляющими переходного процесса 5. Сформулируйте законы коммутации. Поясните, почему ток конденсатора может изменяться скачком, почему напряжение на индуктивности может изменяться скачком. 6. Поясните, какие условия называются начальными и как они определяются. 7. Дайте определение постоянной времени и укажите, как она связана 8. Определите затухание, постоянную времени и длительность переходного процесса при включении последовательной R, L -цепи на постоянное напряжение (Ответ: 9. Объясните, как, вычислив корни характеристического уравнения, можно определить характер переходного процесса. Поясните это (Ответ: характер процесса — колебательный).
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 555; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.91.130 (0.01 с.) |


 . Для простых цепей получается дифференциальное уравнение первого или второго порядка, в котором в качестве искомой величины выбирают либо ток в индуктивном элементе, либо напряжение на емкостном элементе.
. Для простых цепей получается дифференциальное уравнение первого или второго порядка, в котором в качестве искомой величины выбирают либо ток в индуктивном элементе, либо напряжение на емкостном элементе.
 и называют установившимися.
и называют установившимися.
 и называют свободными, а их выражения должны содержать постоянные интегрирования, число которых равно порядку однородного уравнения.
и называют свободными, а их выражения должны содержать постоянные интегрирования, число которых равно порядку однородного уравнения. ,
,  следует найти постоянные интегрирования.
следует найти постоянные интегрирования. происходит мгновенно. При таких коммутациях ток в индуктивном элементе и напряжение на емкостном в начальный момент времени после коммутации
происходит мгновенно. При таких коммутациях ток в индуктивном элементе и напряжение на емкостном в начальный момент времени после коммутации 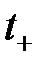 такие же, как в момент времени, непосредственно предшествовавший коммутации
такие же, как в момент времени, непосредственно предшествовавший коммутации  . Эти условия получаются из законов коммутации.
. Эти условия получаются из законов коммутации. (5.1)
(5.1) (5.2)
(5.2) и напряжения на емкостных элементах
и напряжения на емкостных элементах 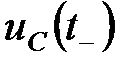 непосредственно перед коммутацией называются начальными условиями.
непосредственно перед коммутацией называются начальными условиями. равны нулю, т.е.
равны нулю, т.е.  ;
;  , то эти условия называются нулевыми начальными условиями. В противном случае получаются ненулевые начальные условия.
, то эти условия называются нулевыми начальными условиями. В противном случае получаются ненулевые начальные условия.
 ,
, , (5.3)
, (5.3)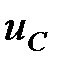 .
. , если подставить выражение
, если подставить выражение  , где
, где  — постоянная интегрирования.
— постоянная интегрирования. 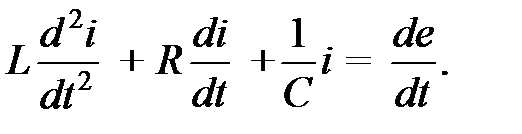 (5.4)
(5.4)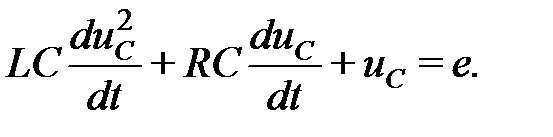 (5.5)
(5.5) ,
, .
. и
и 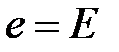 , то согласно схеме (рис. 5.2)
, то согласно схеме (рис. 5.2)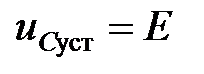 и
и 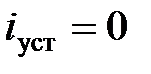 .
. .
.  (5.6)
(5.6)

 и
и  — постоянные интегрирования;
— постоянные интегрирования; и
и  — корни характеристического уравнения
— корни характеристического уравнения

 (5.7)
(5.7) ,
,
 , находим как
, находим как ,
,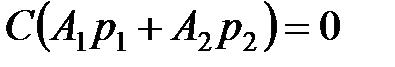 ,
, ,
,  .
. , которые находим как
, которые находим как . (5.8)
. (5.8) , то
, то  комплексные сопряженные корни
комплексные сопряженные корни  , то
, то  и
и  действительные разные корни и процесс будет апериодическим (рис. 5.4 кривая б);
действительные разные корни и процесс будет апериодическим (рис. 5.4 кривая б); , то
, то 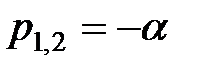 действительные, равные корни и будем иметь предельный случай апериодического процесса (критический) (рис. 5.4 кривая в).
действительные, равные корни и будем иметь предельный случай апериодического процесса (критический) (рис. 5.4 кривая в).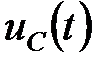 : колебательный (а), апериодический (б), критический (в) режимы
: колебательный (а), апериодический (б), критический (в) режимы (5.9)
(5.9) .
.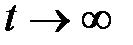 , то получим
, то получим .
. (5.10)
(5.10) ,
, — постоянная интегрирования;
— постоянная интегрирования; — единственный корень характеристического уравнения
— единственный корень характеристического уравнения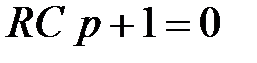 .
. называется постоянной времени заряда. Чем больше
называется постоянной времени заряда. Чем больше  ,
,  переходный процесс практически заканчивается.
переходный процесс практически заканчивается.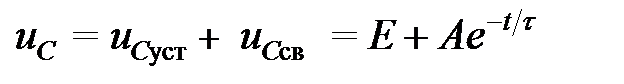 . (5.11)
. (5.11)
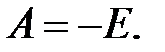
 , (5.12)
, (5.12) , (5.13)
, (5.13)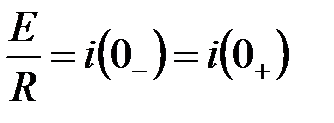 начальное значение тока.
начальное значение тока.
 и тогда
и тогда (5.14)
(5.14)
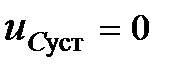 .
. .
. .
.
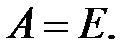
 , (5.15)
, (5.15) (5.16)
(5.16) начальное значение тока.
начальное значение тока.
 цепи
цепи (5.17)
(5.17)
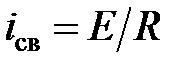 .
. (5.18)
(5.18) ,
, — постоянная интегрирования;
— постоянная интегрирования; — единственный корень характеристического уравнения
— единственный корень характеристического уравнения
 называется постоянной времени процесса.
называется постоянной времени процесса. .
.
 (5.19)
(5.19) (5.20)
(5.20) . (5.21)
. (5.21) в этой цепи изменяется скачком и затем спадает до нуля, в то время как ток и напряжение
в этой цепи изменяется скачком и затем спадает до нуля, в то время как ток и напряжение  монотонно возрастают.
монотонно возрастают.
 определяет скорость переходного процесса нарастания тока или напряжения цепи. Одним из способов определения
определяет скорость переходного процесса нарастания тока или напряжения цепи. Одним из способов определения  является аналитический, когда этот параметр вычисляют по формулам (см. пп. 5.2, 5.4). Другим способом является геометрический, когда
является аналитический, когда этот параметр вычисляют по формулам (см. пп. 5.2, 5.4). Другим способом является геометрический, когда  определяют по касательной, проведенной к точке начала графика изменения тока или напряжения (рис. 5.10). Переходный процесс часто считают практически закончившимся через интервал времени
определяют по касательной, проведенной к точке начала графика изменения тока или напряжения (рис. 5.10). Переходный процесс часто считают практически закончившимся через интервал времени  с момента коммутации, когда величины достигают
с момента коммутации, когда величины достигают 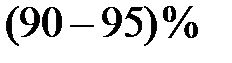 своего максимального изменения.
своего максимального изменения. .
.
 ), дифференциальное уравнение, с током
), дифференциальное уравнение, с током  и проанализируйте его.
и проанализируйте его. Ом,
Ом,  Гн; переходный процесс можно считать законченным, когда ток достигает значения
Гн; переходный процесс можно считать законченным, когда ток достигает значения 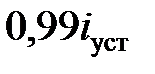 .
.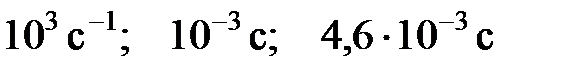 ).
). Ом,
Ом,  Гн,
Гн, мкФ.
мкФ.


